当前位置： 首页 > article >正文

Golang每日一练(leetDay0033) 二叉树专题（2）

article 2024/11/13 6:40:36

目录

97. 交错字符串 Interleaving String  🌟🌟 

98. 验证二叉搜索树 Validate Binary Search Tree  🌟🌟

99. 恢复二叉搜索树 Recover Binary Search Tree  🌟🌟

🌟 每日一练刷题专栏 🌟

Golang每日一练 专栏

Python每日一练 专栏

C/C++每日一练 专栏

Java每日一练 专栏

二叉树专题（2）第97题除外

97. 交错字符串 Interleaving String

给定三个字符串 s1、s2、s3，请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。

两个字符串 s 和 t 交错 的定义与过程如下，其中每个字符串都会被分割成若干 非空 子字符串：

  • s = s1 + s2 + ... + sn
  • t = t1 + t2 + ... + tm
  • |n - m| <= 1
  • 交错 是 s1 + t1 + s2 + t2 + s3 + t3 + ... 或者 t1 + s1 + t2 + s2 + t3 + s3 + ...

注意：a + b 意味着字符串 a 和 b 连接。

示例 1：

输入：s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
输出：true

示例 2：

输入：s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc"
输出：false

示例 3：

输入：s1 = "", s2 = "", s3 = ""
输出：true

提示：

  • 0 <= s1.length, s2.length <= 100
  • 0 <= s3.length <= 200
  • s1、s2、和 s3 都由小写英文字母组成

进阶：您能否仅使用 O(s2.length) 额外的内存空间来解决它?

代码1：动态规划

package main

import (
	"fmt"
)

func isInterleave(s1 string, s2 string, s3 string) bool {
	if len(s1)+len(s2) != len(s3) {
		return false
	}
	dp := make([][]bool, len(s1)+1)
	for i := range dp {
		dp[i] = make([]bool, len(s2)+1)
	}
	dp[0][0] = true
	for i := 1; i <= len(s1); i++ {
		dp[i][0] = dp[i-1][0] && s1[i-1] == s3[i-1]
	}
	for j := 1; j <= len(s2); j++ {
		dp[0][j] = dp[0][j-1] && s2[j-1] == s3[j-1]
	}
	for i := 1; i <= len(s1); i++ {
		for j := 1; j <= len(s2); j++ {
			if s1[i-1] == s3[i+j-1] {
				dp[i][j] = dp[i][j] || dp[i-1][j]
			}
			if s2[j-1] == s3[i+j-1] {
				dp[i][j] = dp[i][j] || dp[i][j-1]
			}
		}
	}
	return dp[len(s1)][len(s2)]
}

func main() {
	s1 := "aabcc"
	s2 := "dbbca"
	s3 := "aadbbcbcac"
	fmt.Println(isInterleave(s1, s2, s3))
	s1 = "aabcc"
	s2 = "dbbca"
	s3 = "aadbbbaccc"
	fmt.Println(isInterleave(s1, s2, s3))
	s1 = ""
	s2 = ""
	s3 = ""
	fmt.Println(isInterleave(s1, s2, s3))
}

输出：

true
false
true

代码2：广度优先搜索

package main

import (
	"fmt"
)

func isInterleave(s1 string, s2 string, s3 string) bool {
	if len(s1)+len(s2) != len(s3) {
		return false
	}
	queue := [][]int{{0, 0}}
	visited := make([][]bool, len(s1)+1)
	for i := range visited {
		visited[i] = make([]bool, len(s2)+1)
	}
	for len(queue) > 0 {
		i, j := queue[0][0], queue[0][1]
		queue = queue[1:]
		if visited[i][j] {
			continue
		}
		visited[i][j] = true
		if i == len(s1) && j == len(s2) {
			return true
		}
		if i < len(s1) && s1[i] == s3[i+j] {
			queue = append(queue, []int{i + 1, j})
		}
		if j < len(s2) && s2[j] == s3[i+j] {
			queue = append(queue, []int{i, j + 1})
		}
	}
	return false
}

func main() {
	s1 := "aabcc"
	s2 := "dbbca"
	s3 := "aadbbcbcac"
	fmt.Println(isInterleave(s1, s2, s3))
	s1 = "aabcc"
	s2 = "dbbca"
	s3 = "aadbbbaccc"
	fmt.Println(isInterleave(s1, s2, s3))
	s1 = ""
	s2 = ""
	s3 = ""
	fmt.Println(isInterleave(s1, s2, s3))
}

98. 验证二叉搜索树 Validate Binary Search Tree

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

  • 节点的左子树只包含 小于 当前节点的数。
  • 节点的右子树只包含 大于 当前节点的数。
  • 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

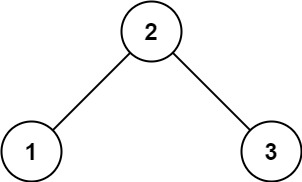
输入：root = [2,1,3]
输出：true

示例 2：

输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

  • 树中节点数目范围在[1, 10^4] 内
  • -2^31 <= Node.val <= 2^31 - 1

代码1：

package main

import (
	"fmt"
)

const null = -1 << 31

type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

func isValidBST(root *TreeNode) bool {
	var pre *TreeNode
	return validate(root, &pre)
}

func validate(node *TreeNode, pre **TreeNode) bool {
	if node == nil {
		return true
	}
	if !validate(node.Left, pre) {
		return false
	}
	if *pre != nil && node.Val <= (*pre).Val {
		return false
	}
	*pre = node
	return validate(node.Right, pre)
}

func buildTree(nums []int) *TreeNode {
	if len(nums) == 0 {
		return nil
	}
	root := &TreeNode{Val: nums[0]}
	Queue := []*TreeNode{root}
	idx := 1
	for idx < len(nums) {
		node := Queue[0]
		Queue = Queue[1:]
		if nums[idx] != null {
			node.Left = &TreeNode{Val: nums[idx]}
			Queue = append(Queue, node.Left)
		}
		idx++
		if idx < len(nums) && nums[idx] != null {
			node.Right = &TreeNode{Val: nums[idx]}
			Queue = append(Queue, node.Right)
		}
		idx++
	}
	return root
}

func (root *TreeNode) LevelOrder() []int {
	var res []int
	if root == nil {
		return res
	}
	Queue := []*TreeNode{root}
	for len(Queue) > 0 {
		cur := Queue[0]
		Queue = Queue[1:]
		res = append(res, cur.Val)
		if cur.Left != nil {
			Queue = append(Queue, cur.Left)
		}
		if cur.Right != nil {
			Queue = append(Queue, cur.Right)
		}
	}
	return res
}

func main() {
	nums := []int{2, 1, 3}
	root := buildTree(nums)
	fmt.Println(isValidBST(root))
	nums = []int{5, 1, 4, null, null, 3, 6}
	root = buildTree(nums)
	fmt.Println(isValidBST(root))
	nums = []int{3, 1, 5, null, null, 4, 6}
	root = buildTree(nums)
	fmt.Println(isValidBST(root))
}

输出：

true
false
true

代码2： 递归法

package main

import (
	"fmt"
)

const null = -1 << 31

type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

func isValidBST(root *TreeNode) bool {
	return validate(root, nil, nil)
}

func validate(node *TreeNode, min *int, max *int) bool {
	if node == nil {
		return true
	}
	if (min != nil && node.Val <= *min) || (max != nil && node.Val >= *max) {
		return false
	}
	return validate(node.Left, min, &node.Val) && validate(node.Right, &node.Val, max)
}

func buildTree(nums []int) *TreeNode {
	if len(nums) == 0 {
		return nil
	}
	root := &TreeNode{Val: nums[0]}
	Queue := []*TreeNode{root}
	idx := 1
	for idx < len(nums) {
		node := Queue[0]
		Queue = Queue[1:]
		if nums[idx] != null {
			node.Left = &TreeNode{Val: nums[idx]}
			Queue = append(Queue, node.Left)
		}
		idx++
		if idx < len(nums) && nums[idx] != null {
			node.Right = &TreeNode{Val: nums[idx]}
			Queue = append(Queue, node.Right)
		}
		idx++
	}
	return root
}

func main() {
	nums := []int{2, 1, 3}
	root := buildTree(nums)
	fmt.Println(isValidBST(root))
	nums = []int{5, 1, 4, null, null, 3, 6}
	root = buildTree(nums)
	fmt.Println(isValidBST(root))
	nums = []int{3, 1, 5, null, null, 4, 6}
	root = buildTree(nums)
	fmt.Println(isValidBST(root))
}

 代码3： 中序遍历+判断

package main

import (
	"fmt"
)

const null = -1 << 31

type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

func isValidBST(root *TreeNode) bool {
	var pre *TreeNode
	stack := []*TreeNode{}
	for root != nil || len(stack) > 0 {
		for root != nil {
			stack = append(stack, root)
			root = root.Left
		}
		node := stack[len(stack)-1]
		stack = stack[:len(stack)-1]
		if pre != nil && node.Val <= pre.Val {
			return false
		}
		pre = node
		root = node.Right
	}
	return true
}

func buildTree(nums []int) *TreeNode {
	if len(nums) == 0 {
		return nil
	}
	root := &TreeNode{Val: nums[0]}
	Queue := []*TreeNode{root}
	idx := 1
	for idx < len(nums) {
		node := Queue[0]
		Queue = Queue[1:]
		if nums[idx] != null {
			node.Left = &TreeNode{Val: nums[idx]}
			Queue = append(Queue, node.Left)
		}
		idx++
		if idx < len(nums) && nums[idx] != null {
			node.Right = &TreeNode{Val: nums[idx]}
			Queue = append(Queue, node.Right)
		}
		idx++
	}
	return root
}

func main() {
	nums := []int{2, 1, 3}
	root := buildTree(nums)
	fmt.Println(isValidBST(root))
	nums = []int{5, 1, 4, null, null, 3, 6}
	root = buildTree(nums)
	fmt.Println(isValidBST(root))
	nums = []int{3, 1, 5, null, null, 4, 6}
	root = buildTree(nums)
	fmt.Println(isValidBST(root))
}

99. 恢复二叉搜索树 Recover Binary Search Tree

给你二叉搜索树的根节点 root ，该树中的 恰好 两个节点的值被错误地交换。请在不改变其结构的情况下，恢复这棵树 。

示例 1：

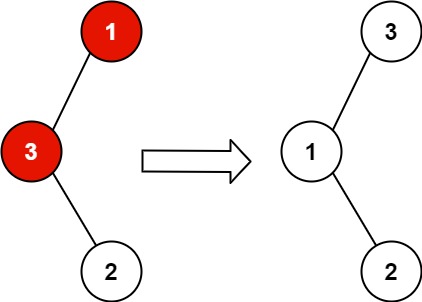
输入：root = [1,3,null,null,2]
输出：[3,1,null,null,2]
解释：3 不能是 1 的左孩子，因为 3 > 1 。交换 1 和 3 使二叉搜索树有效。

示例 2：

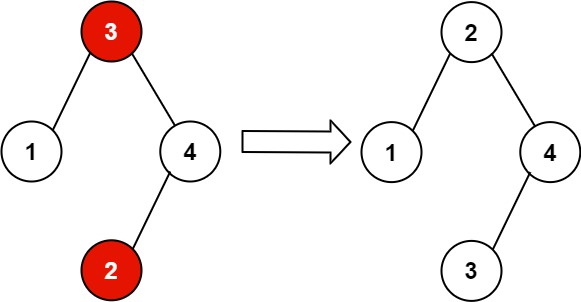
输入：root = [3,1,4,null,null,2]
输出：[2,1,4,null,null,3]
解释：2 不能在 3 的右子树中，因为 2 < 3 。交换 2 和 3 使二叉搜索树有效。

提示：

  • 树上节点的数目在范围 [2, 1000] 内
  • -2^31 <= Node.val <= 2^31 - 1

进阶：使用 O(n) 空间复杂度的解法很容易实现。你能想出一个只使用 O(1) 空间的解决方案吗？

代码1：中序遍历+交换节点值

对于二叉搜索树，中序遍历得到的序列是递增的。因此，如果有两个节点的值被错误地交换了，那么在中序遍历序列中一定存在两个相邻的逆序对。具体做法是，在中序遍历的过程中，用一个变量pre记录上一个遍历到的节点，每次遍历到一个节点时，判断其值是否小于pre的值，如果小于，则说明存在逆序对，记录下这两个节点，并继续遍历。最后，交换这两个节点的值即可。

package main

import (
	"fmt"
	"strconv"
)

const null = -1 << 31

type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

func recoverTree(root *TreeNode) {
	var pre, first, second *TreeNode
	var stack []*TreeNode
	for root != nil || len(stack) > 0 {
		for root != nil {
			stack = append(stack, root)
			root = root.Left
		}
		node := stack[len(stack)-1]
		stack = stack[:len(stack)-1]
		if pre != nil && node.Val < pre.Val {
			if first == nil {
				first = pre
			}
			second = node
		}
		pre = node
		root = node.Right
	}
	first.Val, second.Val = second.Val, first.Val
}

func buildTree(nums []int) *TreeNode {
	if len(nums) == 0 {
		return nil
	}
	root := &TreeNode{Val: nums[0]}
	Queue := []*TreeNode{root}
	idx := 1
	for idx < len(nums) {
		node := Queue[0]
		Queue = Queue[1:]
		if nums[idx] != null {
			node.Left = &TreeNode{Val: nums[idx]}
			Queue = append(Queue, node.Left)
		}
		idx++
		if idx < len(nums) && nums[idx] != null {
			node.Right = &TreeNode{Val: nums[idx]}
			Queue = append(Queue, node.Right)
		}
		idx++
	}
	return root
}

func levelOrder(root *TreeNode) string {
	if root == nil {
		return "[]"
	}
	arr := []int{}
	que := []*TreeNode{root}
	for len(que) > 0 {
		levelSize := len(que)
		for i := 0; i < levelSize; i++ {
			node := que[0]
			que = que[1:]
			if node == nil {
				arr = append(arr, null)
				continue
			}
			arr = append(arr, node.Val)
			que = append(que, node.Left, node.Right)
		}
	}
	size := len(arr)
	for size > 0 && arr[size-1] == null {
		arr = arr[:size-1]
		size = len(arr)
	}
	result := "["
	for i, n := range arr {
		if n == null {
			result += "null"
		} else {
			result += strconv.FormatInt(int64(n), 10)
		}
		if i < size-1 {
			result += ","
		} else {
			result += "]"
		}
	}
	return result
}

func main() {
	nums := []int{1, 3, null, null, 2}
	root := buildTree(nums)
	fmt.Println(levelOrder(root))
	recoverTree(root)
	fmt.Println(levelOrder(root))

	nums = []int{3, 1, 4, null, null, 2}
	root = buildTree(nums)
	fmt.Println(levelOrder(root))
	recoverTree(root)
	fmt.Println(levelOrder(root))
}

输出：

[1,3,null,null,2]
[3,1,null,null,2]

[3,1,4,null,null,2]
[2,1,4,null,null,3]

代码2：Morris遍历

Morris遍历是一种不需要额外空间的遍历二叉树的方法，它的核心思想是利用叶子节点的空指针来存储遍历中的临时信息。对于二叉搜索树，Morris中序遍历的过程中，每个节点的左子树都已经被遍历完毕，因此可以在遍历到每个节点时，比较它的值和它的前驱节点的值，如果它的值小于前驱节点的值，那么就找到了一个逆序对。我们用两个指针first和second来记录这两个节点，最后交换它们的值即可。

package main

import (
	"fmt"
	"strconv"
)

const null = -1 << 31

type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

func recoverTree(root *TreeNode) {
	var first, second, pre *TreeNode
	var temp *TreeNode
	for root != nil {
		if root.Left != nil {
			temp = root.Left
			for temp.Right != nil && temp.Right != root {
				temp = temp.Right
			}
			if temp.Right == nil {
				temp.Right = root
				root = root.Left
			} else {
				if pre != nil && root.Val < pre.Val {
					if first == nil {
						first = pre
					}
					second = root
				}
				pre = root
				temp.Right = nil
				root = root.Right
			}
		} else {
			if pre != nil && root.Val < pre.Val {
				if first == nil {
					first = pre
				}
				second = root
			}
			pre = root
			root = root.Right
		}
	}
	first.Val, second.Val = second.Val, first.Val
}

func buildTree(nums []int) *TreeNode {
	if len(nums) == 0 {
		return nil
	}
	root := &TreeNode{Val: nums[0]}
	Queue := []*TreeNode{root}
	idx := 1
	for idx < len(nums) {
		node := Queue[0]
		Queue = Queue[1:]
		if nums[idx] != null {
			node.Left = &TreeNode{Val: nums[idx]}
			Queue = append(Queue, node.Left)
		}
		idx++
		if idx < len(nums) && nums[idx] != null {
			node.Right = &TreeNode{Val: nums[idx]}
			Queue = append(Queue, node.Right)
		}
		idx++
	}
	return root
}

func levelOrder(root *TreeNode) string {
	if root == nil {
		return "[]"
	}
	arr := []int{}
	que := []*TreeNode{root}
	for len(que) > 0 {
		levelSize := len(que)
		for i := 0; i < levelSize; i++ {
			node := que[0]
			que = que[1:]
			if node == nil {
				arr = append(arr, null)
				continue
			}
			arr = append(arr, node.Val)
			que = append(que, node.Left, node.Right)
		}
	}
	size := len(arr)
	for size > 0 && arr[size-1] == null {
		arr = arr[:size-1]
		size = len(arr)
	}
	result := "["
	for i, n := range arr {
		if n == null {
			result += "null"
		} else {
			result += strconv.FormatInt(int64(n), 10)
		}
		if i < size-1 {
			result += ","
		} else {
			result += "]"
		}
	}
	return result
}

func main() {
	nums := []int{1, 3, null, null, 2}
	root := buildTree(nums)
	fmt.Println(levelOrder(root))
	recoverTree(root)
	fmt.Println(levelOrder(root))

	nums = []int{3, 1, 4, null, null, 2}
	root = buildTree(nums)
	fmt.Println(levelOrder(root))
	recoverTree(root)
	fmt.Println(levelOrder(root))
}

🌟 每日一练刷题专栏 🌟

✨ 持续，努力奋斗做强刷题搬运工！

👍 点赞，你的认可是我坚持的动力！ 

🌟 收藏，你的青睐是我努力的方向！ 

✎ 评论，你的意见是我进步的财富！  

☸ 主页：https://hannyang.blog.csdn.net/ 

Golang每日一练 专栏

Python每日一练 专栏

C/C++每日一练 专栏

Java每日一练 专栏


http://www.kler.cn/a/10125.html

相关文章：

  • Python的Web请求：requests库入门与应用
  • JavaScript——函数、事件与BOM对象
  • 关于Oracle数据库密码复杂度检查的一些概念
  • 动手学深度学习68 Transformer
  • Select，poll，epoll和IO多路复用和NIO
  • 2024AAAI | DiffRAW: 利用扩散模型从手机RAW图生成单反相机质量的RGB图像
  • c#多线程
  • 人工智障对话日记1：为狗写诗
  • 面试官在线改简历 | 只有6秒！程序员简历这样写才能抓住科技公司大佬的眼球
  • pdf转换成word怎么转换？这个方法一学就会!
  • C语言文件操作复习回顾（1）
  • 基于STM32的倒车雷达系统设计
  • JAVA解析XML时的内存消耗问题
  • IronOCR for .NET crack,IronOCR的独特功能
  • CMake入门教程【核心篇】8.0构建目标
  • 2023-03-18青少年软件编程（C语言）等级考试试卷（一级）解析
  • 是时候告别这些 Python 库了
  • 你真的会用background属性？
  • 【51单片机Task】：led十六进制控制led灯详解、按键控制流水灯、跑马灯等任务
  • x210官方uboot配置编译
  • DNS服务器配置
  • 机器学习和深度学习在气象中的应用（台风预报只能订正、风速预报订正、LSTM 方法预测 ENSO）
  • 基于Spring boot和Vue3的博客平台:系统通知、评论回复通知、专栏更新通知、用户角色与权限管理模块
  • 数据技术嘉年华星光璀璨，云和恩墨全栈数据技术能力闪耀会场
  • Vue实现自动化平台（五）--用例编辑页面
  • ​InnoDB引擎之flush脏页​