AB测试基本原理
AB测试基本原理
- AB测试
- AB测试的基本步骤
- 1、AB测试的基本步骤
- ①选取指标
- 指标的分类
- ②建立假设
- ③选取实验单位
- ④计算样本量
- ⑤流量分割
- ⑥实验周期计算
- ⑦线上验证
- ⑧数据检验
AB测试
- 所谓的AB测试就是使用实验组和对照组,通过控制变量法保证实验组和对照组基本条件一致,在实验组上增加变量,看是否引起显著变化。
- AB测试是互联网行业常用的归因分析方法,用来评估某个策略或者变化引起的效果。从理论上来说,AB测试是基于假设检验为理论依据的,就是我们先对实验组&对照组是否有显著差异提出假设,通过试验后的数据进行验证,判断是否显著差别。
AB测试的基本步骤
1、AB测试的基本步骤
AB测试一般分成8个步骤,具体如下。
①选取指标
在建立AB实验前,我们需要明确我的实验目的是什么,或者改动点是什么。并对应落到哪些指标上,但是需要注意,所选取的指标能够很好的衡量实验的目的,而且需要对指标进行分级,唯一核心指标+其他观察指标。
- 核心指标:核心指标用来衡量实验的效果。
- 观察指标:用来观察实验对其他指标的影响。
指标的分类
指标按照来源不同,可以分为绝对值类和比率类指标,我们这里区分不同类型观测指标,主要因为在接下来的样本量计算中,这两类指标的样本计算有所差别:
-
绝对值类指标。我们平常直接计算就能得到的单个指标,不需要多个指标计算得到。一般都是统计该指标在一段时间内的均值或者汇总值,比如DAU,平均停留时长等。这类指标一般较少作为AB测试的观测指标。
-
比率类指标。与绝对值类指标相对应,我们不能直接计算得到,而是通过多个指标计算得到。比如某页面的点击率,我们需要先计算页面的点击数和展现数,两者相除才能得到该指标。类似的,还有一些转化率、复购率等等。AB测试观测的大部分指标都是比率类指标。
为什么这里要区分不同类型的观测指标,因为在接下来的样本量计算中,这两类指标的样本量计算有所差别。
②建立假设
由于AB测试的理论基础是基于假设检验的,所以需要建立假设,即提出原假设和备选假设。
- 原假设H0:实验组&对照组 实验改动后指标是相同的,无差异的。
- 备选假设H1:实验组&对照组 实验改动后指标是不同的,有差异的。
原假设和备选假设都是基于第一步的选取指标来假设的。
③选取实验单位
在实验中我们一般使用用户粒度的实验单位,但总体有3中选择粒度:
- 用户粒度
这个是最推荐的,即以一个用户的唯一标识来作为实验样本。好处是符合AB测试的分桶单位唯一性,不会造成一个实验单位处于两个分桶,造成的数据不置信。 - 设备粒度
以一个设备标识为实验单位。相比用户粒度,如果一个用户有两个手机,那么也可能出现一个用户在两个分桶中的情况,所以也会造成数据不置信的情况。 - 行为粒度
以一次行为为实验单位,也就是用户某一次使用该功能,是实验桶,下一次使用可能就被切换为基线桶。会造成大量的用户处于不同的分桶。强烈不推荐这种方式。
④计算样本量
该步骤是要避免流量浪费,高效利用流量,把可用流量分到其他试验。另外还要避免在统计功效不足的情况下给出错误结论。即避免实验过程种,流量使用过多或者过少的情况。
计算样本量的理论基础主要基于大数定律和中心极限定理,
- 大数定律:当试验条件不变时,随机试验重复多次以后,随机事件的频率近似等于随机事件的概率。
- 中心极限定理:对独立同分布且有相同期望和方差的n个随机变量,当样本量很大时,样本的均值近似服从标准正态分布N(0,1)。
每一组的实验样本数量计算如下:
N
=
(
Z
(
1
−
α
2
)
+
Z
1
−
β
)
2
∗
σ
2
δ
2
,
N= \frac{(Z_{(1-\frac{\alpha}{2})}+Z_{1-\beta})^2*\sigma^2}{\delta^2},
N=δ2(Z(1−2α)+Z1−β)2∗σ2,
其中,
σ
代表的是样本数据的标准差,衡量的是整体样本数据的波动性,可以计算样本的标准差计算得到。
其中,\sigma代表的是样本数据的标准差,衡量的是整体样本数据的波动性,可以计算样本的标准差计算得到。
其中,σ代表的是样本数据的标准差,衡量的是整体样本数据的波动性,可以计算样本的标准差计算得到。
而
δ
代表的是预期实验组和对照组两组数据的差值
,
比如期望点击率从
20
%
提升到
25
%
,那么
δ
就是
5
%
。
而\delta代表的是预期实验组和对照组两组数据的差值,比如期望点击率从20\%提升到25\%,那么\delta就是5\%。
而δ代表的是预期实验组和对照组两组数据的差值,比如期望点击率从20%提升到25%,那么δ就是5%。
α
和
β
也就是我们在统计学中提到的,犯第一类错误和第二类错误的概率,通常
α
取值
0.05
,即置信度是
(
1
−
α
)
是
0.95
%
;
β
取值
0.2
,即统计功效的取值(
1
−
β
)是
0.8
。
\alpha和\beta也就是我们在统计学中提到的,犯第一类错误和第二类错误的概率,通常\alpha取值0.05,即置信度是(1-\alpha)是0.95\%;\beta取值0.2,即统计功效的取值(1-\beta)是0.8。
α和β也就是我们在统计学中提到的,犯第一类错误和第二类错误的概率,通常α取值0.05,即置信度是(1−α)是0.95%;β取值0.2,即统计功效的取值(1−β)是0.8。
在上述公式中,截至到目前只有 σ \sigma σ还没进行解释,当观测指标为绝对值/比率指标时,样本的标准差的计算公式会略有不同:
- 当观测值为绝对值时:
σ 2 = 2 ∗ Σ 1 n ( x i − x ˉ ) 2 n − 1 , 其中 n 为样本量, x ˉ 为样本均值 \sigma^2=\frac{2*\Sigma_{1}^{n}(x_{i}-\bar{x})^2}{n-1},其中n为样本量,\bar{x}为样本均值 σ2=n−12∗Σ1n(xi−xˉ)2,其中n为样本量,xˉ为样本均值 - 当观测指标为比率类指标时:
σ 2 = P A ( 1 − P A ) + P B ( 1 − P B ) ,其中: P A , P B 分别对照组合实验组的观测数据 \sigma^2 = P_{A}(1-P_A)+P_B(1-P_B),其中:P_A,P_B分别对照组合实验组的观测数据 σ2=PA(1−PA)+PB(1−PB),其中:PA,PB分别对照组合实验组的观测数据
其中 P A P_A PA、 P B P_B PB分别为对照组合实验组的观测数据,例如,我们希望点击率从20%提升到25%,那么 P A = 20 % , P B = 25 % , δ = 5 % P_A=20\%,P_B=25\%,\delta=5\% PA=20%,PB=25%,δ=5%
在实际工作中,可以不用那么复杂,有现成的计算网页,我们可以直接线上计算连接

⑤流量分割
在实际的运营中,流量是稀缺资源,产品迭代时代时,会有很多AB测试需要同时做,而产品的流量又是有限的,因此需要对流量进行充分切割。主要可以分成“分流”、“分层”,“分桶”。
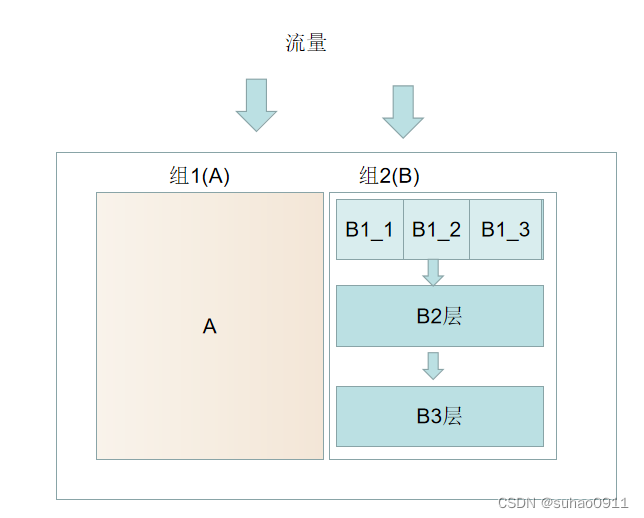
- 分流(互斥)
用户分流是指将整体分成几块,例如上图中把流量分成组1(A)和组2(B)两组,主要特征是分流的结果是互斥的,一个用户只能被分到一个组中,组1+组2 = 100%流量。划分的目的,是为了更好的进行互不干扰的实验测试。但是当同时进行多个实验的时候,这种方法就可能不太满足需求了。 - 分层(正交)
同一分流可以分成多个分层,例如分流组2分成了3层,B1=B2=B3,流量从B1进入下一层中用户随机分桶,进行实验,每桶的用户质量一致,即我们说的正交。分层的前提是各个实验层之间无业务关联,保证这一批用户都均匀的分布到所有实验层中,达到用户正交的效果。 - 分桶(互斥与正交)
我们在同时进行多个实验的时候,会在层中进行分组实验,例如上图中B1层分成了B1_1、B1_2、B1_3等3个桶,这三个桶彼此是互斥的,且和B2、B3层正交的。
⑥实验周期计算
实验周期通常由最小样本量、可以接受实验桶的大小比例以及周活决定的。
实验时长
=
最小样本量
∗
实验桶比例
周活
实验时长 = \frac{最小样本量*实验桶比例}{周活}
实验时长=周活最小样本量∗实验桶比例
此外还需要考虑一些用户周期的情况,例如用户在工作日和周末特征不一样的情况,那么周期就需要1个完成周。
⑦线上验证
这一步很显然,就是根据上述一些步骤把实验部署到线上,然后进行实验。
⑧数据检验
绝对值指标推荐使用T检验,相对指标推荐使用Z检验,当多组测试时推荐使用方差检验。
需要统计的结果:diff,P值,置信区间。
- 计算P值
也就计算当H0假设成立时,观测到样本数据出现的概率。在统计学上,将5%作为小概率时间,所以一般用5%来对比计算出来的P值。当P值小于5%时,拒绝H0假设,即两个指标不同,反过来,当P值大于5%时,不拒绝H0 假设。 - 计算置信区间
一般情况下,我们都会用95%来作为置信水平,也就是说,当前数据的估计,有95%的区间包含了总体参数的真值。
