已知原根多项式和寄存器初始值时求LFSR的简单例子
线性反馈移位寄存器(LFSR)是一种用于生成伪随机数序列的简单结构。在这里,我们有一个四项原根多项式 p ( x ) = 1 + x + 0 x 2 = 11 0 2 p(x) = 1 + x + 0x^2 = 110_2 p(x)=1+x+0x2=1102 和初始值 S 0 = 100 S_0 = 100 S0=100。我们将使用 LFSR 动作过程来生成一个伪随机序列。
LFSR 的动作过程如下:
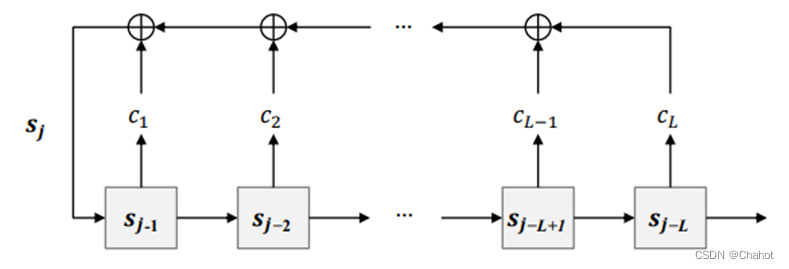
将初始值加载到寄存器中。
对于每次时钟周期:
a. 将寄存器中的当前值与原根多项式的非零项进行异或(XOR)操作。
b. 将结果右移一位,然后将异或(XOR)操作的结果放入最高位。
现在,我们将详细描述 LFSR 的动作过程:
加载初始值:
S
0
=
100
S_0 = 100
S0=100。
时钟周期 1:
a. 异或操作:
1
⊕
0
=
1
1 \oplus 0 = 1
1⊕0=1, 作用目标是寄存器从左到右的第一第二位
b. 右移并更新最高位:
S
1
=
110
S_1 = 110
S1=110。
时钟周期 2:
a. 异或操作:
1
⊕
1
=
0
1 \oplus 1 = 0
1⊕1=0。
b. 右移并更新最高位:
S
2
=
011
S_2 = 011
S2=011。
时钟周期 3:
a. 异或操作:
0
⊕
1
=
1
0 \oplus 1 = 1
0⊕1=1。
b. 右移并更新最高位:
S
3
=
101
S_3 = 101
S3=101。
时钟周期 4:
a. 异或操作:
1
⊕
0
=
1
1 \oplus 0 = 1
1⊕0=1。
b. 右移并更新最高位:
S
4
=
110
S_4 = 110
S4=110。从这一位开始进入循环
在时钟周期 4 后,寄存器的值回到了初始值运算后的第一个计算值
S
1
=
110
S_1 = 110
S1=110,因此序列将开始重复。所以,LFSR 生成的伪随机序列为:
100,110,011,101,110,…
