LeetCode 64.最小路径和(开辟额外空间(二维)、不开辟额外空间(二维)、优化(一维))
Problem: 64. 最小路径和
文章目录
- 前言
- 思路
- 解题方法
- Code
- 优化:
前言
简单写写自己对这道题的拙见,如有意见或者建议可以联系笔者owo
思路
这道题就是典型的填格子,对于这类题目在看到的时候需要抓住我这个位置状态是依赖于哪几个数据继续构造,然后将构造的数据填入到格子中。这个格子后续会被其他格子依赖,依此类推,这样下去当整个表都填完的时候,答案就出来了。
解题方法
观察这个题目例子这个表:

根据题意,我们只能选择右走or下走,然后还要把路径上的和全部加起来找最小路径和。
这里我们需要注意的是,动态规划本身就是从小问题推到大问题,小问题中就能知道大问题的规律,所以如何从小问题中发现规律就是我们学习动态规划的关键。
在这道题目中,我们可以观察到,我的某个位置的数据要么从左边来要么从上边来,也就是:Math.min(左,上)。但是由于第一行和第一列只有右方向or下方向,所以这两条路线的路径和应该为下图所示:

现在问题来了,我中间那些格子的值该如何填???
注意,我们这里反复强调了,能走的方向只有右or下,那么很自然,我们格子的值就应该是左or下推导出来,如下图:

递推公式为:f(x) = Math.min(左,上)+value
其他格子的值也是如此,左上依赖,所以到这里代码就很容易写出来了…
(我这里提供两个版本的dp)
Code
class Solution {
public int minPathSum(int[][] grid) {
//return dp(grid);
return dp2(grid);
}
// 创建额外空间
public int dp(int[][] grid){
int n = grid.length;
int m = grid[0].length;
int[][] dp = new int[n][m];
dp[0][0] = grid[0][0];
for(int i = 1; i < n; i++){
dp[i][0] = dp[i-1][0] + grid[i][0];
}
for(int i = 1; i < m; i++){
dp[0][i] = dp[0][i-1] + grid[0][i];
}
for(int i = 1; i < n; i++){
for(int j = 1; j < m; j++){
dp[i][j] = Math.min(dp[i-1][j],dp[i][j-1])+grid[i][j];
}
}
return dp[n-1][m-1];
}
// 无需额外空间版本
public int dp2(int[][] grid){
int n = grid.length;
int m = grid[0].length;
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
if(i == 0 && j == 0){
continue;
}
if(i == 0){
grid[i][j] += grid[i][j-1];
}else if(j == 0){
grid[i][j] += grid[i-1][j];
}else{
grid[i][j] += Math.min(grid[i-1][j],grid[i][j-1]);
}
}
}
return grid[n-1][m-1];
}
}
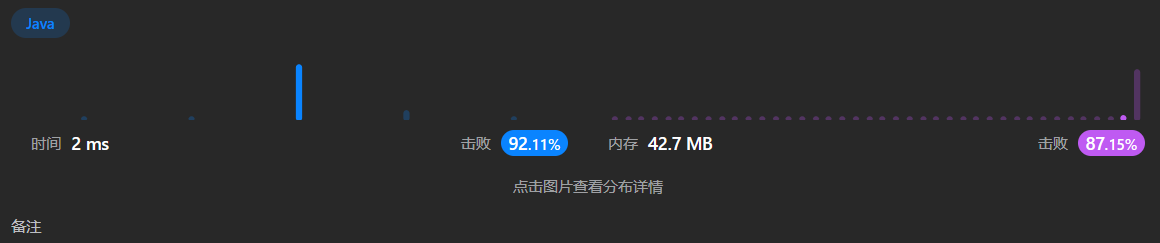
运行结果:
优化:
这里的优化是针对需要额外空间的版本来介绍
其实不难注意到,假如我们的填格子的顺序为一层一层来的话,就意味着,我们当前层依赖完上一层数据后,上一层数据对我们的意义已经不大了,可以被取舍掉。这样就可以做到空间上的优化,使用一维数组进行dp
过程图如下:
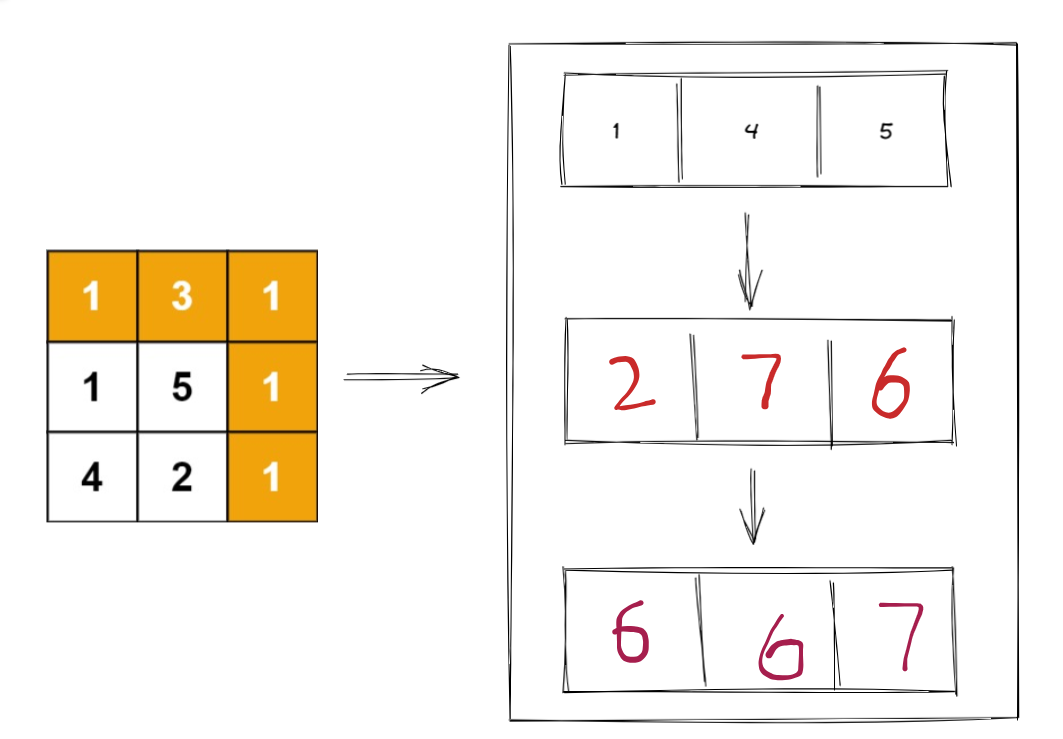
代码实现如下:
class Solution {
public int minPathSum(int[][] grid) {
return dp(grid);
}
public int dp(int[][] grid){
int m = grid.length;
int n = grid[0].length;
int[] dp = new int[n];
dp[0] = grid[0][0];
for(int i = 1; i < n; i++){
dp[i] = dp[i-1] + grid[0][i];
}
for(int i = 1; i < m; i++){
// 每一层都从0下标开始,但是0-1=-1是越界的,所以要保证dp[j]取的上方向的值
for(int j = 0; j < n; j++){
dp[j] = Math.min(dp[j],(j==0?Integer.MAX_VALUE:dp[j-1]))+grid[i][j];
}
}
return dp[n-1];
}
}
