基于PyTorch的MNIST手写体分类实战
第2章对MNIST数据做了介绍,描述了其构成方式及其数据的特征和标签的含义等。了解这些有助于编写合适的程序来对MNIST数据集进行分析和识别。本节将使用同样的数据集完成对其进行分类的任务。
3.1.1 数据图像的获取与标签的说明
MNIST数据集的详细介绍在第2章中已经完成,读者可以使用相同的代码对数据进行获取,代码如下:
import numpy as np
x_train = np.load("./dataset/mnist/x_train.npy")
y_train_label = np.load("./dataset/mnist/y_train_label.npy")
基本数据的获取与第2章类似,这里就不过多阐述了,不过需要注意的是,在第2章介绍数据集时只使用了图像数据,没有对标签进行说明,在这里重点对数据标签,也就是y_train_label进行介绍。
我们可以使用下面语句打印出数据集的前10个标签:
print(y_train_label[:10])结果如下:
import numpy as np
import torch
x_train = np.load("./dataset/mnist/x_train.npy")
y_train_label = np.load("./dataset/mnist/y_train_label.npy")
x = torch.tensor(y_train_label[:5],dtype=torch.int64)
# 定义一个张量输入,因为此时有 5 个数值,且最大值为9,类别数为10
# 所以我们可以得到 y 的输出结果的形状为 shape=(5,10),即5行12列
y = torch.nn.functional.one_hot(x, 10) # 一个参数张量x,10为类别数
ptint(y)
结果如下:
tensor([[0, 0, 0, 0, 0, 1, 0, 0, 0, 0],
[1, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 1]])
可以看到,one_hot的作用是将一个序列转换成以one_hot形式表示的数据集。所有的行或者列都被设置成0,而每个特定的位置都对应一个1来表示,如图3-1所示。

图3-1 one_hot形式表示的数据集
对于MNIST数据集的标签来说,这实际上就是一个60 000幅图片的60 000×10大小的矩阵张量[60 000,10]。前面的数指的是数据集中图片的个数为60 000个,后面的10指的是10个列向量。
下面使用PyTorch 2.0框架完成手写体的识别。
3.1.2 模型的准备(多层感知机)
在第2章已经讲过了,PyTorch最重要的一项内容是模型的准备与设计,而模型的设计最关键的一点就是了解输出和输入的数据结构类型。
通过第2章有关图像去噪的演示,读者已经了解了我们的输入数据格式是一个[28,28]大小的二维图像。而通过对数据结构的分析,我们可以知道,对于每个图形都有一个确定的分类结果,也就是0~10的一个确定数字。
下面将按这个想法来设计模型。从前面对图像的分析来看,对整体图形进行判别的一个基本想法就是将图像作为一个整体直观地进行判别,因此基于这种解决问题的思路,简单的模型设计就是同时对图像所有参数进行计算,即使用一个多层感知机(Multi-Layer Perceptron,MLP)对图像进行分类。整体的模型设计结构如图3-2所示。
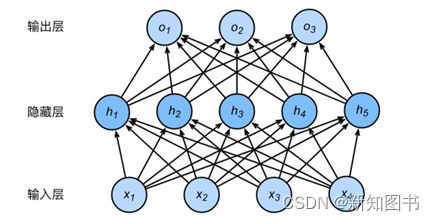
图3-2 整体的模型设计结构
从图3-2可以看到,一个多层感知机模型就是将数据输入后,分散到每个模型的节点(隐藏层),进行数据计算后,再将计算结果输出到对应的输出层中。多层感知机的模型结构如下:
class NeuralNetwork(nn.Module):
def __init__(self):
super(NeuralNetwork, self).__init__()
self.flatten = nn.Flatten()
self.linear_relu_stack = nn.Sequential(
nn.Linear(28*28,312),
nn.ReLU(),
nn.Linear(312, 256),
nn.ReLU(),
nn.Linear(256, 10)
)
def forward(self, input):
x = self.flatten(input)
logits = self.linear_relu_stack(x)
return logits
3.1.3 损失函数的表示与计算
第2章使用了MSELoss作为目标图形与预测图形的损失值,而在本例中,我们需要预测的目标是图形的“分类”,而不是图形表示本身,因此我们需要寻找并使用一种新的能够对类别归属进行“计算”的函数。
本例所使用的交叉熵损失函数为torch.nn.CrossEntropyLoss。PyTorch官方网站对其介绍如下:
CLASS torch.nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=- 100,reduce=None, reduction='mean', label_smoothing=0.0)该损失函数计算输入值(Input)和目标值(Target)之间的交叉熵损失。交叉熵损失函数CrossEntropyLoss可用于训练单类别或者多类别的分类问题。给定参数weight时,会为传递进来的每个类别的计算数值重新加载一个修正权重。当数据集分布不均衡时,这是很有用的。
同样需要注意的是,因为torch.nn.CrossEntropyLoss内置了Softmax运算,而Softmax的作用是计算分类结果中最大的那个类。从图3-3所示的对PyTorch 2.0中CrossEntropyLoss的实现可以看到,此时CrossEntropyLoss已经在计算的同时实现了Softmax计算,因此在使用torch.nn.CrossEntropyLoss作为损失函数时,不需要在网络的最后添加Softmax层。此外,label应为一个整数,而不是One-Hot编码形式。
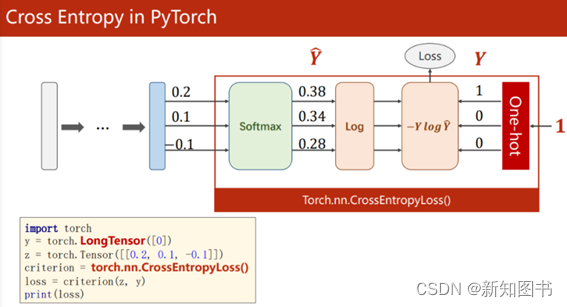
图3-3 使用torch.nn.CrossEntropyLoss()作为损失函数
CrossEntropyLoss示例代码如下:
import torch
y = torch.LongTensor([0])
z = torch.Tensor([[0.2,0.1,-0.1]])
criterion = torch.nn.CrossEntropyLoss()
loss = criterion(z,y)
print(loss)
CrossEntropyLoss的数学公式较为复杂,建议学有余力的读者查阅相关内容进行学习,目前只需要掌握这方面内容即可。
3.1.4 基于PyTorch的手写体识别的实现
下面介绍基于PyTorch的手写体识别的实现。通过前文的介绍,我们还需要定义深度学习的优化器部分,在这里采用Adam优化器,相关代码如下:
model = NeuralNetwork()
optimizer = torch.optim.Adam(model.parameters(), lr=2e-5) #设定优化函数
在这个实战案例中首先需要定义模型,之后将模型参数传入优化器中,lr是对学习率的设定,根据设定的学习率进行模型计算。完整的手写体识别模型如下:
import os
os.environ['CUDA_VISIBLE_DEVICES'] = '0' #指定GPU编号
import torch
import numpy as np
from tqdm import tqdm
batch_size =320#设定每次训练的批次数
epochs=1024 #设定训练次数
#device="cpu" #PyTorch的特性,需要指定计算的硬件,如果没有GPU,就使用CPU进行计算
device="cuda" #在这里默认使用GPU,如果读者运行出现问题,可以将其改成CPU模式
#设定的多层感知机网络模型
class NeuralNetwork(torch.nn.Module):
def __init__(self):
super(NeuralNetwork, self).__init__()
self.flatten = torch.nn.Flatten()
self.linear_relu_stack = torch.nn.Sequential(
torch.nn.Linear(28*28,312),
torch.nn.ReLU(),
torch.nn.Linear(312, 256),
torch.nn.ReLU(),
torch.nn.Linear(256, 10)
)
def forward(self, input):
x = self.flatten(input)
logits = self.linear_relu_stack(x)
return logits
model = NeuralNetwork()
model = model.to(device) #将计算模型传入GPU硬件等待计算
model = torch.compile(model) #PyTorch 2.0的特性,加速计算速度
loss_fu = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=2e-5) #设定优化函数
#载入数据
x_train = np.load("../../dataset/mnist/x_train.npy")
y_train_label = np.load("../../dataset/mnist/y_train_label.npy")
train_num = len(x_train)//batch_size
#开始计算
for epoch in range(20):
train_loss = 0
for i in range(train_num):
start = i * batch_size
end = (i + 1) * batch_size
train_batch = torch.tensor(x_train[start:end]).to(device)
label_batch = torch.tensor(y_train_label[start:end]).to(device)
pred = model(train_batch)
loss = loss_fu(pred,label_batch)
optimizer.zero_grad()
loss.backward()
optimizer.step()
train_loss += loss.item() # 记录每个批次的损失值
# 计算并打印损失值
train_loss /= train_num
accuracy = (pred.argmax(1) == label_batch).type(torch.float32).sum().item() / batch_size
print("train_loss:", round(train_loss,2),"accuracy:",round(accuracy,2))
此时模型的训练结果如图3-4所示。

图3-4 模型的训练结果
可以看到随着模型循环次数的增加,模型的损失值在降低,而准确率在增高,具体请读者自行验证测试。
本文节选自《PyTorch 2.0深度学习从零开始学》。

