论文阅读 - Learning Human Interactions with the Influence Model

NIPS'01 早期模型
要求知识背景: 似然函数,极大似然估计、HMM、期望最大化
目录
1 Introduction
2 The Facilitator Room
3 T h e I n f l u e n c e M o d e l
3 . 1 ( R e ) i n t r o d u c i n g t h e I n f l u e n c e M o d e l
3 . 2 L e a r n i n g f o r t h e I n f l u e n c e M o d e l
3. 2. 1 期望——影响力最大化模型
3. 2. 2 观察到的影响力模型
3. 2. 3 综合数据观察到的影响模型的评估
4 实验及结果
我们有兴趣对对话环境中人与人之间的互动进行定量建模。虽然有多种模型可能是合适的,如耦合 HMM,但所有模型都需要大量参数来描述链之间的交互。作为替代方案,我们提出了[1]中开发的生成模型--"影响模型",该模型通过对具有恒定 "影响 "参数的成对转换进行凸组合来参数化隐藏状态转换概率。
我们为这一模型开发了一种学习算法,并利用合成数据展示了与其他标准模型相比,该模型建立链式依赖关系模型的能力。我们还展示了将该模型应用于人类交互数据的早期结果。
1 Introduction
在社会科学领域,旨在理解个体之间的互动并影响其行为的工作由来已久。在心理学界,有很多研究这些影响的案例。例如,Wells 和 Petty [2] 的研究表明,听众反复点头会极大地影响演讲者的自信心。这类研究让我们对人类动态的运作有了有趣的认识。在许多情况下,实验人员可以通过观察任务的完成情况或问卷的回答,对行为的变化进行量化测量。然而,这种方法无法捕捉到行为的一些重要方面--一个人对另一个人的行为的影响程度、互动的强度等等。迄今为止,实验者一直依赖于基于手写注释的定性测量("比尔在这节课上和苏珊谈得更多 "或 "乔非常生气,总是对简大喊大叫")或轶事。这样做有很多问题--很难确切知道实验者的测量结果是什么意思,更难比较不同研究的结果。我们的目标是提供一种量化这些效果的方法。我们的专业背景是计算机视觉、语音处理和机器学习,我们相信,有了相关工具,我们就能在实现这一目标方面取得一些进展。本文是我们对这些复杂交互作用建模的首次探索。
我们工作的一般场景涉及许多参与者之间的互动,以及许多可能影响他们行为的动作器。起初,我们只希望观察和模拟人与动作器之间的相互影响,从而分析和预测他们的行为。从长远来看,我们希望利用这些模型建立反馈系统,根据分析结果应用动作器。通过这种方式闭环,最终将形成一个影响人类行为的随机模型。理想情况下,这将使我们能够加强人与人之间的互动(例如,防止打架、增进理解、促进讨论)。虽然我们离这个目标还很遥远,但我们希望这些初步研究能在理解人类互动方面取得一些进展。为此,我们目前正在使用一种特殊的实验装置,我们称之为 "促进者房间"(Facilitator Room)。
虽然有许多可能的临时方法来计算每种效应的特征(如交互强度),但我们希望开发一种通用框架,以便分析受试者相互影响以及实验变量影响受试者的所有效应。Chalee Asivathiratham 在他的博士论文[1]中提出的 "影响模型 "是一种生成模型,是表示多个马尔可夫链相互影响的一种可能方法。正如我们将在第 3 节中描述的,这个模型似乎非常适合我们感兴趣的效应建模。在本文中,我们用隐藏状态/观测值对模型进行了概括,并开发了一种从数据中学习其参数的算法(第 3.2 节)。然后,我们利用合成数据展示了该算法和模型与其他模型的性能比较。在第 4 节中,我们展示了将我们的模型应用于主持人室互动场景的早期结果。最后,我们将提出初步结论和未来工作计划。
2 The Facilitator Room
为了研究人与人之间的互动以及各种实验变量的影响,我们开发了一种实验装置,我们称之为 “协调员室"。这个房间是一个 15 英尺乘 15 英尺的空间,里面有三张沙发和一张桌子。房间里安装了六台云台变焦摄像机和一系列麦克风。通过这些传感器,我们可以估算出说话速度、语音音调、相对语音能量、基于区域的运动能量和圆球跟踪等特征。使用所有传感器时,数据传输速率为 1.9 千兆字节/小时。在第 4 节描述的实验中,我们使用了传感器的一个子集,结果数据速率为 1.1G/小时,持续两小时。
房间里还安装了许多执行器,用于影响参与者的行为。目前,我们在每个座位后面都安装了扬声器,目的是用白噪声掩盖声音,对个人耳语物品等。我们还在每个座位上安装了灯光,灯光的颜色和强度由计算机控制。目的是改变整个房间的照明条件,并对个人进行聚光,以影响其他人对他们的反应。房间里有五台投影仪:三台在墙上,一台通向主屏幕,一台放在桌子上。这些投影仪的作用是在适当的时候播放相关信息,以改变谈话模式。
在本文的实验中,我们只是开始利用这个房间的潜力--此时我们还没有使用执行器。然而,在对个体间的基线互动进行建模之前,我们无法研究执行器的影响,因此在本研究中,我们将重点放在后者上。
3 T h e I n f l u e n c e M o d e l
为了寻找一个适合我们目标的模型,我们转向了图形模型界有关动态贝叶斯网(DBN)的工作(有关 DBN 的综述见 [3])。最直接的方法是用 HMM 为每个参与者建模,然后求所有状态空间的外积。遗憾的是,状态数将与链数 N 成指数关系,其中 Q 是每条链的状态数,即 Q^N,而转换矩阵中的参数数为 Q^2N。此外,很难解释所得到模型的参数--例如,很难确定某个人是否对另一个人产生了影响。
文献 [4] 和 [5] 所描述的用于成对链的耦合 HMM 是一种潜在的解决方案,因为它可以模拟一条链的状态对两条链之前状态的依赖性,即![]() ,如图 1 (a)所示。这样,状态空间保持在 2N,每条链有 QxQxQ 个转移表,每条链共有 2Q^3 个转移参数。
,如图 1 (a)所示。这样,状态空间保持在 2N,每条链有 QxQxQ 个转移表,每条链共有 2Q^3 个转移参数。

图 1:时间 t-1 和 t 时显示的可能的人类交互 DBN 模型:(a)耦合 HMM,(b)具有 N 个链的耦合 HMM 的广义版本,以及(c)耦合 HMM 的成对链。
将此模型推广到 N 个链时,下一个状态取决于之前所有状态的值,即我们应该估计![]() 然而,这需要为每个链建立一个 Q^NxQ 转移表,从而产生 NQ^{N+1} 个过渡矩阵参数,这仍然非常庞大。另一种方法是用标准耦合 HMM 模拟所有可能的链对。这种方案仍然需要
然而,这需要为每个链建立一个 Q^NxQ 转移表,从而产生 NQ^{N+1} 个过渡矩阵参数,这仍然非常庞大。另一种方法是用标准耦合 HMM 模拟所有可能的链对。这种方案仍然需要 个转移表参数。由于我们希望在相当短的片段(如一小段对话)中对这些参数进行估计,因此我们希望将参数数量保持在最低水平,从而继续寻找合适的模型。
3 . 1 ( R e ) i n t r o d u c i n g t h e I n f l u e n c e M o d e l
Asavathiratham [1] 在他的论文中提出了 "影响模型",这是一种生成模型,用于描述许多马尔可夫链之间的联系,其简单参数化为每个链对其他链的 "影响"。他的研究表明,涉及大量链之间相互作用的复杂现象可以通过这种简化模型模拟出来,例如美国电网中发电站的上/下行时间。在他的描述中,所有状态都被观测到,而且他没有开发出学习模型参数的机制。因此,我们在名义上扩展了他的模型,增加了隐藏状态和观测的概念。我们还在第 3.2 节中开发了一种参数学习算法。
影响模型的图形模型与广义 N 链耦合 HMM 的图形模型相同,但有一个非常重要的简化。我们不再保留整个![]() , 我们只保留
, 我们只保留![]() 并将前者近似为:
并将前者近似为:

换句话说,我们通过对条件概率的凸组合来形成给定链下一状态的分布。因此,我们每条链只有 N个QxQ 表和 N个α 个参数,总共有 NQ^2 + N^2 个转移参数。这比上述任何模型的参数都要少得多。当然,真正的问题是,我们是否保留了足够的建模能力来确定参与者之间的相互作用。
阿萨瓦蒂拉塔姆将 α 称为 "影响",因为它们是恒定因子,告诉我们特定链的状态转换在多大程度上取决于特定的邻链。重要的是要认识到这些因素恒定的后果:直观地说,这意味着我们受邻居影响的程度是恒定的,但我们如何受邻居影响则取决于邻居的状态。另一种看法是,我们只是在模拟邻居对我们影响的一阶效应:如果乔的吼叫肯定会导致我们安静,而马克的吼叫肯定会导致我们吼回去,并且两者的 α 值相等,那么两者的吼叫将导致我们下一步行动的分布,其概率质量在吼叫和不吼叫之间平均分布。
这就是我们所放弃的建模能力--虽然全连接耦合 HMM 可以让我们明确地模拟乔和马克一起大喊大叫这一联合事件的影响,但影响模型却不能(但要注意,成对耦合 HMM 也不能模拟这种联合影响)。
这种简化对于人际交往领域似乎是合理的,对于许多其他领域也可能是合理的。此外,它还为我们提供了一小套可解释的参数--α 值--概括了链之间的相互作用。通过估算这些参数,我们可以了解这些链条相互影响的程度。
在下面的章节中,我们将为该模型开发一种学习算法,并通过合成数据和真实数据展示该模型可以捕捉到的互动结构类型。最后,虽然我们没有在本文中进行探讨,但我们可以很容易地使用该模型来估计执行者对参与者的影响。我们只需为每个执行者创建一个新的(观察到的)链,然后观察其影响。在这种情况下,要研究执行者是如何改变参与者的行为的,我们必须查看概率表以及 α 's
3 . 2 L e a r n i n g f o r t h e I n f l u e n c e M o d e l
从数据中估计影响模型的问题可表述如下。我们得到了来自每个链 i 的观测序列 。我们的目标是估算链 j 对链 i 的影响程度
,以及描述这种链间影响的成对条件概率分布
![]() 。在本节中,我们将开发实现这一目标的方法,并用合成数据加以说明。
。在本节中,我们将开发实现这一目标的方法,并用合成数据加以说明。
3. 2. 1 期望——影响力最大化模型
在图 2 中,我们展示了具有隐藏状态和连续观测数据的最一般形式的影响模型的图形模型。

(图 2:(a) 广义耦合 HMM,(b) 带有隐藏状态的影响模型,(c) 带有观测状态的影响模型的图。)
要将该模型拟合到数据中,我们需要最大化影响模型在其自由参数上的似然。似然函数可以简便地写成

估计模型参数的一种方法是期望最大化。E 步要求我们计算 ![]() ,这在大多数情况下相当于应用结点树算法(精确推理)或某种近似推理方案(变异推理等)。我们将在后面讨论在这个模型上进行推理的可能性。 M 步是该模型的特殊步骤,要求最大化 E 步得到的下限。通过观察这一表达式,我们可以发现,除了 α_{ij} 参数外,其他所有参数的 M 步骤与 HMM 只有微不足道的差别。不过,我们可以很容易地写出 α_{ij} 的更新方程,注意到它们是 N 个条件概率表的混合权重,类似于高斯混合。α_{ij} 更新方程是按照高斯混合的 M 步骤推导得出的(即引入一个隐藏状态来代表 "活跃 "的混合分量,然后对其充分统计量进行期望):
,这在大多数情况下相当于应用结点树算法(精确推理)或某种近似推理方案(变异推理等)。我们将在后面讨论在这个模型上进行推理的可能性。 M 步是该模型的特殊步骤,要求最大化 E 步得到的下限。通过观察这一表达式,我们可以发现,除了 α_{ij} 参数外,其他所有参数的 M 步骤与 HMM 只有微不足道的差别。不过,我们可以很容易地写出 α_{ij} 的更新方程,注意到它们是 N 个条件概率表的混合权重,类似于高斯混合。α_{ij} 更新方程是按照高斯混合的 M 步骤推导得出的(即引入一个隐藏状态来代表 "活跃 "的混合分量,然后对其充分统计量进行期望):

![]() 事件表示在 t 时刻链 i 受到链 j 的影响,而
事件表示在 t 时刻链 i 受到链 j 的影响,而 ![]() 事件表示在 t 时刻链 i 处于状态 k。
事件表示在 t 时刻链 i 处于状态 k。
3. 2. 2 观察到的影响力模型
由于进行 E 步所需的推理困难重重,我们决定简化估计问题,允许观察每条链的状态 (见图 2)。我们决定通过将 HMM 拟合到每条链的观测值并进行维特比解码来获得状态序列。然后,根据这些状态序列直接估算链转移表(通过频率计数)就很容易了。由于我们的目标是估算链间影响(通过
's),因此这种观测和链转换参数的 "钳制 "有助于解决完整模型的过拟合问题。
现在,我们有了一个不寻常的 DBN,其中的观测节点具有很强的相互连接,而隐藏状态却没有。这给推理带来了严重的问题,因为将观测状态节点边际化会导致所有隐藏状态在所有时间和所有链上完全相连。除非我们采用一种近似方法,成功地将这些节点解耦,否则最大化程序(如 EM)是不可行的。不过,有一种简单得多的方法可以估计我们观察到的情况中的 值。让我们先来看看对于观察到的影响模型,似然函数是如何简化的:

将这一表达式转换为对数似然,并去除与 最大化无关的项,即可得出:

我们可以通过保留与链 i 相关的项来进一步简化这一表达式:
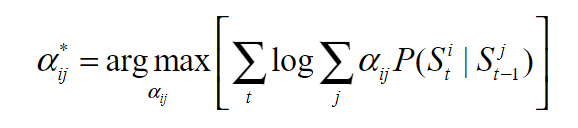
每条链的似然值在 中呈凹形,这一点可以很容易地证明如下:

那么每条链的可能性就变成:
这是凹的,因为对于任何![]()
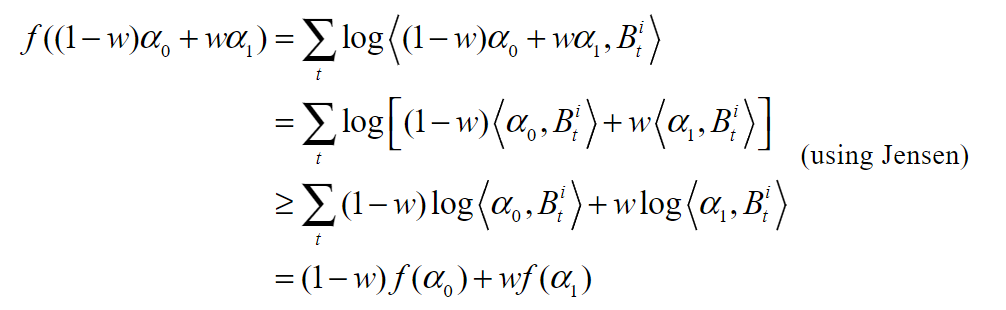
现在取导数 w.r.t.
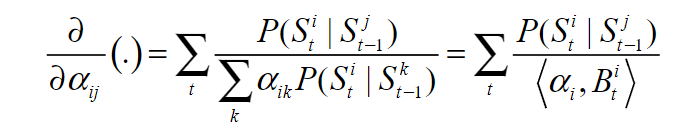
请注意,只要对条件概率表进行适当的重新排列,形成 向量,上述梯度和每链似然表达式的计算并不复杂。 再加上每条链的可能性是凹的,可行的
's 空间是凸的,这意味着这个优化问题是完全一维搜索的受限梯度上升的教科书式案例(见 [6] 第 29 页)。此外,在本文的所有示例中,20 次迭代足以确保收敛,这相当于不到 10 秒的 CPU 时间。
3. 2. 3 综合数据观察到的影响模型的评估
为了评估我们学习算法的有效性,我们首先展示了合成数据的结果。这些数据由一个影响模型生成,其中有 3 个步调一致的链条:一个是随机演化的领导者(即平面过渡表),另两个是一丝不苟地跟随领导者的追随者(即链条 2 的影响为 1,自我影响为 0)。我们对该模型进行采样,以获得每个链 50 个时间步的训练序列。这些状态序列随后被用于训练另一个随机初始化的影响模型。如上所述,![]() 通过计数估算,α_{ij} 's 通过梯度上升估算。图 3 显示了影响图和一个典型的样本序列。请注意 "跟随 "行为是如何通过该模型准确学习到的--链 1 和链 3 完全跟随链 2。
通过计数估算,α_{ij} 's 通过梯度上升估算。图 3 显示了影响图和一个典型的样本序列。请注意 "跟随 "行为是如何通过该模型准确学习到的--链 1 和链 3 完全跟随链 2。

图 3:在锁步合成数据上测试影响模型的评估流程:(a)t 和 t+1 时生成模型的图形(b)训练序列(c)学习到的影响(α's)--线条的粗细与影响的大小相对应。请注意,链 2 对链 1 和链 3 的强烈影响是正确学习到的。(d) 已学习模型的路径样本。请注意链 1 和 3(跟随者)是如何完全跟随链 2 的
我们还使用 EM 对这些数据评估了广义耦合 HMM(即完整的状态转换表,而不是成对表的混合),并使用结点树算法进行推理。我们再次从锁步模型中采样,并随机初始化模型。图 4 显示了从生成的模型中提取的样本序列。

图 4:在锁步合成数据上测试广义耦合 HMM 的评估流程:(a)生成模型的图形(b)训练序列(c)学习模型的图形和 EM 迭代的似然值(d)学习模型的样本路径。请注意,该模型无法完美捕捉锁步行为,从链 1 在链 2 之后的误差中可以看出这一点。
在这种情况下,学习到的模型表现还算不错,但由于需要估计的参数较多,因此无法完美地学习到 "跟随 "行为![]() 。
。
4 实验及结果
在合成数据上验证了我们算法的性能后,我们在协调室的自然人类互动数据上测试了我们的模型。我们记录了五位参与者玩互动辩论游戏的两小时数据。这个名为 "观点 "的游戏有一叠卡片,上面有不同的有争议的辩论主题。我们为实验录制了 10 个游戏(辩论环节)。为了确保我们能看到所有可能的对局者之间的辩论,我们列出了所有对局者的名单,并从名单中选择了对局者,没有替换。名单上的第一位参与者掷骰子选择一方(正方或反方)。每位辩手的发言时间为一分钟,一分钟后开放舞台供所有参与者讨论。在游戏过程中,参与者的互动方式不受限制。从数据中自动计算出的特征包括每人的运动能量(30 赫兹)、语言能量(30 赫兹)和发声状态(60 赫兹)。此外,在所有游戏中,说话者的轮次(即谁在什么时候说话)都是手工标注的。
在第一项实验中,我们只使用了手写标注的轮流发言。每个玩家都有两种状态--说话和沉默。当多个玩家同时说话时,所有玩家都被视为处于说话状态。游戏的全套特征是所有玩家的二进制状态向量,然后对其进行非均匀重采样,以去除连续重复的状态。因此,如果所有玩家在 t 个时间步中都处于相同的状态,那么这 t 个相同的观察结果实际上被一个时间步所取代。这就有效地分解了数据,使每个对话回合都有一个特征向量。如果不以这种方式对特征进行重采样,自我过渡将压倒人与人之间的影响。
我们估算了整个数据集(全部十个游戏)以及每个游戏的影响矩阵 α。在这个数据集中,玩家 Tammy 总是被要求对玩家 Bob 做出回应/反应,因此我们认为 Bob 对 Tammy 有很大的影响。我们可以从图 5 所示的完整游戏影响矩阵中看到这种影响。此外,在所有数据集中,塔米和安妮都是占主导地位的发言人。这在学习图谱中表现为与其他参与者的紧密联系。. 最后,对于每个游戏,我们将学习到的影响图与手工标记的互动矩阵生成的影响图进行比较。如果参与者 B 对参与者 A 作出了回应,则通过创建从参与者 A 到参与者 B 的有向链接来形成后一种影响图;链接的强度与 B 对 A 作出回应的次数成正比(按 A 的所有影响者归一化)。图 6 显示了我们数据集中游戏子集的结果。

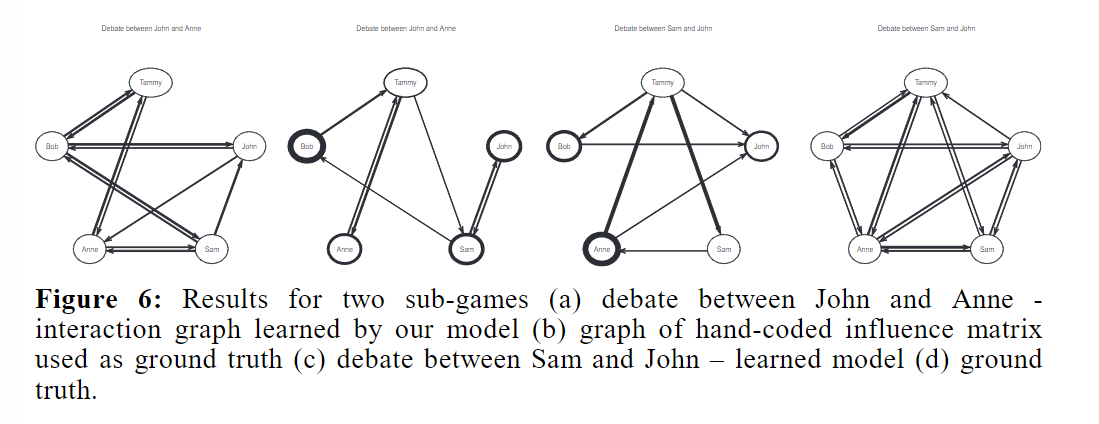
图 6:两个子游戏的结果 (a) 约翰和安妮之间的辩论--我们的模型学习到的交互图 (b) 作为基本事实使用的手工编码影响矩阵图 (c) 萨姆和约翰之间的辩论--学习到的模型 (d) 基本事实。
最后,我们使用每个人的运动能量、语音能量和发声状态运行算法来生成影响图,现在是以无监督的方式学习状态。图 7 显示了提取出的影响结构的一个示例,该示例显示了支持者和对手之间的紧密联系,这在该游戏的视听记录中可以观察到。
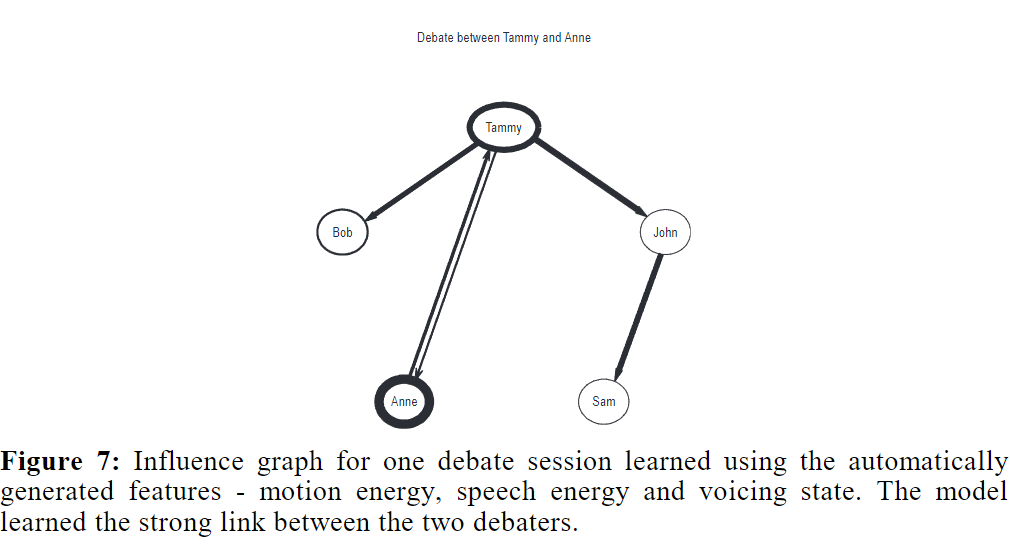
图 7:使用自动生成的特征--动作能量、语言能量和发声状态--学习到的一场辩论的影响图。模型了解到两位辩手之间的紧密联系。
