力扣每日一题73：矩阵置零

题目描述：

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。

示例 1：

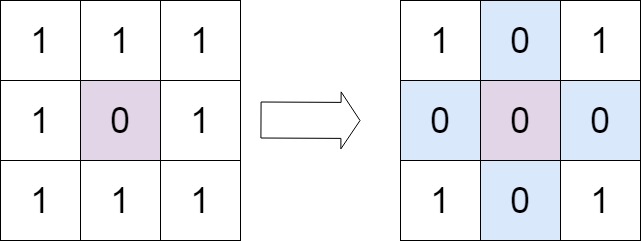
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

示例 2：

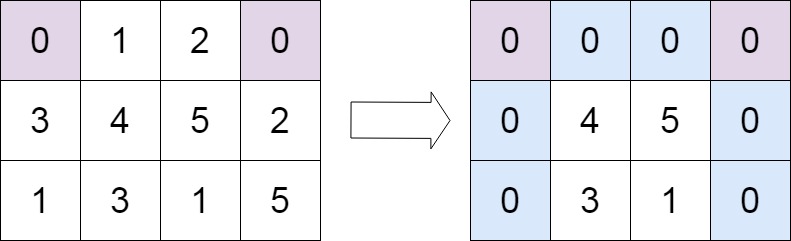
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

提示：

• m == matrix.length
• n == matrix[0].length
• 1 <= m, n <= 200
• -231 <= matrix[i][j] <= 231 - 1

进阶：

• 一个直观的解决方案是使用  O(mn) 的额外空间，但这并不是一个好的解决方案。
• 一个简单的改进方案是使用 O(m + n) 的额外空间，但这仍然不是最好的解决方案。
• 你能想出一个仅使用常量空间的解决方案吗？

通过次数

286.9K

提交次数

446.4K

通过率

64.3%

思路和题解：

一、先遍历一次矩阵，用一个数组row和一个数组col标记要置零的行和列，随后再遍历一次矩阵，如果矩阵所在行或列要置0，那就变零。时间复杂度O(m*n)，空间复杂度O(m+n)

代码：

class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        int m=matrix.size();
        int n=matrix[0].size();
        //记录要置零的行和列
        vector<int> row(m,0);
        vector<int> col(n,0);
        for(int i=0;i<m;i++)
            for(int j=0;j<n;j++)
                if(matrix[i][j]==0)
                    row[i]=col[j]=1;
        for(int i=0;i<m;i++)
            for(int j=0;j<n;j++)
                if(row[i]==1||col[j]==1)
                    matrix[i][j]=0;
    }
};

二、方法一的改进，矩阵的第一行和第一列代替col和row，实现O(1)空间复杂度，但矩阵的第一行和第一列有交叉，交叉的位置既要标记第一行是否出现零，又要标记第一列是否出现零，所以我们应该额外设置一个变量flag，flag与matrix[0][0]一个标记第一行是否出现零，一个标记第一列是否出现零。

代码：

lass Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        int m=matrix.size();
        int n=matrix[0].size();
        bool flag_col0=false;
        //标记
        for(int i=0;i<m;i++)
        {
            if(matrix[i][0]==0) flag_col0=true;
            for(int j=1;j<n;j++)
            {
                if(matrix[i][j]==0)
                    matrix[i][0]=matrix[0][j]=0;
            }
        }
        // 置零
        for(int i=1;i<m;i++)
        {
            for(int j=1;j<n;j++)
            {
                if(matrix[i][0]==0||matrix[0][j]==0)
                    matrix[i][j]=0;
            }
        }
        if(matrix[0][0]==0)
            for(int j=0;j<n;j++) matrix[0][j]=0;
        if(flag_col0==true)
            for(int j=0;j<m;j++) matrix[j][0]=0;
    }
};