当前位置：首页 > article >正文

leetCode 260.只出现一次的数字 ||| + 位运算

article 2024/11/13 15:09:25

260. 只出现一次的数字 III - 力扣（LeetCode）

给你一个整数数组 nums，其中恰好有两个元素只出现一次，其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。你必须设计并实现线性时间复杂度的算法且仅使用常量额外空间来解决此问题。

【问题思考】待解决问题(O_O)?举个栗子：xorSum -> 110，需要找到异或和中的某个值为 1 的比特位，如何解决？

方式1：计算 lowbit ,只保留二进制最低位的1，举个栗子：

 s = 101100
~s = 010011 
(~s)+1 = 010100 // 根据补码的定义，这就是-s 最低 1 左侧取反，右侧不变
s & -s = 000100 // lowbit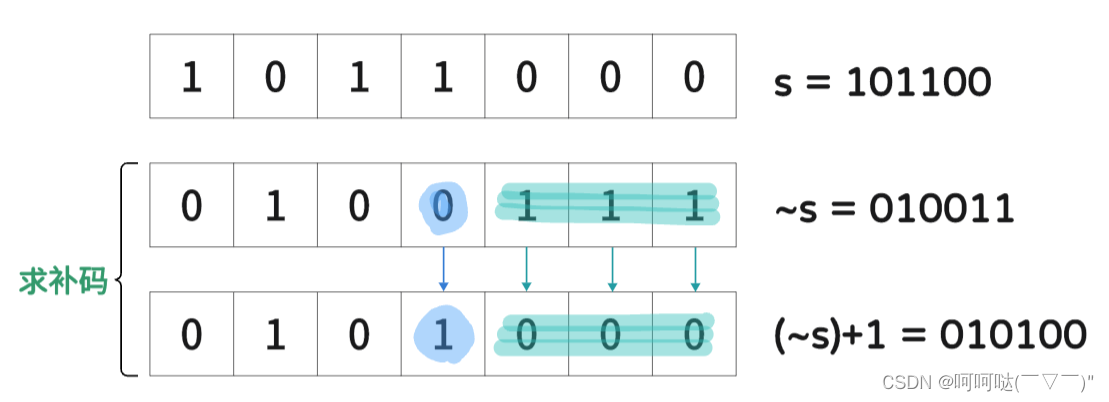

s 和 ~s 若相与，为0

【求补码】：（~s）+ 1，可以简易操作成，其实就是从~s（取反）的结果上，从左到右，直到找到一个0后面都是连续1的子序列的位置，将其设置为1，而后面连续的1的子序列全置为0。这是求补码这个过程。然后再让 s & (~s+1) 就可以获得lowbit。

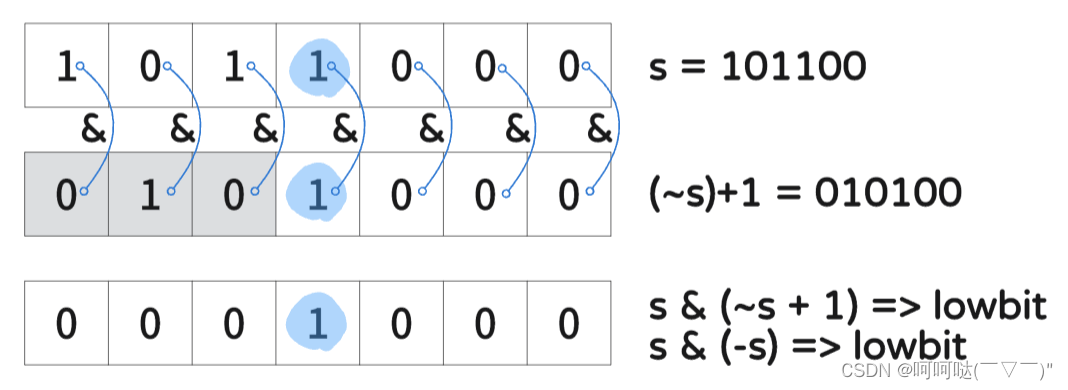
【问题思考(O_O)?】为什么s & (~s+1) 就可以获得 lowbit？原理是什么？

结合上图来看，在取反的结果（~s）上找从左到右出现 0 的最低位位置，而这个位置的左边仍然是保持 s 取反后的结果，也就是和 s 相与还是为0。那我们将 ~s 的这个位置设置为 1，其后的设置为 0，那么 s & (~s+1) 自然就可以找到 s 出现 1 的最低位置，也就可以获得lowbit了。（因为你找到取反后的结果的 0 出现的最低位置，那么就可以通过运算变换求出 s 出现 1 的最低位置，而这恰好有求补码的过程，那么我们也可以进一步将求补码的过程简洁写成 -s ）。具体操作如下：

① 求补码
② s & s的补码 => lowbit，即 s & (~s + 1)

【一个有意思的点】根据补码的定义，就是 -s，那么

② s & (-s) => lowbit

方式2：计算 s尾零的个数，直接取 nums[i] 在该比特位上的值，从而避免逻辑判断

（1）根据 方式1：计算 lowbit ,只保留二进制最低位的1

class Solution {
public:
    vector<int> singleNumber(vector<int>& nums) {
        vector<int>res;
        unsigned int xorSum = 0; //C++ 不需要防止溢出，用 unsigned int
        int type1=0,type2=0;
        for (const int &num: nums) {
            xorSum ^= num;
        }
        // -xorSum 等价于 对xorSum求补码，操作就是取反后加一
        // int lowbit = xorSum & (~xorSum+1);
        int lowbit = xorSum & -xorSum; 
        for (const int &num: nums) {
            //进行分组
            //把值为1的数分为一组
            if(num & lowbit) type1^=num;
            //把值为0的数分为一组
            else type2^=num;

        }
        return {type1, type2};
    }
};

用一个vector容器来存放 type1 和 type2，也可以省去逻辑判断(if...else...)

        ...
        ...
        int type1=0,type2=0;

        int lowbit = xorSum & -xorSum; 
       
        for (const int &num: nums) {
            if(num & lowbit) type1^=num; //把值为1的数分为一组
            else type2^=num; //把值为0的数分为一组
        }
        return {type1, type2};
    }
};
-------------------------------------------------------------------------------------
        ...
        ...
        vector<int> arr(2);
        for (const int &num: nums) {
            arr[(num & lowbit)!=0] ^=num; // (num & lowbit)!=0 => true(1) or false(0)
        }
        return arr;
    }
};

于是就有如下代码：

class Solution {
public:
    vector<int> singleNumber(vector<int>& nums) {
        unsigned int xorSum = 0; //C++ 不需要防止溢出，用 unsigned int
        
        for (const int &num: nums) {
            xorSum ^= num;
        }

        // -xorSum 等价于 对xorSum求补码，操作就是取反后加一
        // int lowbit = xorSum & (~xorSum+1);
        int lowbit = xorSum & -xorSum; 
       
        vector<int> arr(2);
        for (const int &num: nums) {
            arr[(num & lowbit)!=0] ^=num; // (num & lowbit)!=0 => true(1) or false(0)
        }
        return arr;
    }
};

（2）根据方式2：计算 s尾零的个数，直接取 nums[i] 在该比特位上的值，从而避免逻辑判断

C++ __builtin_系列函数___builtin_ctz-CSDN博客https://blog.csdn.net/yandaoqiusheng/article/details/102920785__builtin_ctz(x) ：返回 x 的二进制下前导的 0 的个数

class Solution {
public:
    vector<int> singleNumber(vector<int>& nums) {
        unsigned int xorSum = 0; //C++ 不需要防止溢出，用 unsigned int
        for (const int &num: nums) {
            xorSum ^= num;
        }
        int ctz = __builtin_ctz(xorSum);
        vector<int> arr(2);
        for (const int &num: nums) {
            arr[(num >> ctz) & 1] ^=num; 
        }
        return arr;
    }
};

时间复杂度：O(n)，其中 n 为 nums 的长度
空间复杂度：O(1)，仅用到若干额外变量

参考和推荐文章：

260. 只出现一次的数字 III - 力扣（LeetCode）https://leetcode.cn/problems/single-number-iii/solutions/2484352/tu-jie-yi-zhang-tu-miao-dong-zhuan-huan-np9d2/分享｜从集合论到位运算，常见位运算技巧分类总结！ - 力扣（LeetCode）https://leetcode.cn/circle/discuss/CaOJ45/

查看全文

http://www.kler.cn/a/108771.html