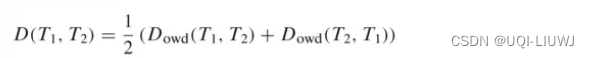轨迹相似度整理
1 基于点之间的距离
1.1 欧几里得距离
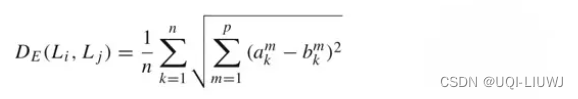
- 优点:线性计算时间
- 缺点:轨迹长度必须一样
1.2 DTW
DTW 笔记: Dynamic Time Warping 动态时间规整 (&DTW的python实现) 【DDTW,WDTW】_UQI-LIUWJ的博客-CSDN博客
- 缺点:对noise比较敏感
'Exact Indexing of Dynamic Time Warping' VLDB 2002
1.3 LCSS 最长公共子序列
文巾解题1143. 最长公共子序列_UQI-LIUWJ的博客-CSDN博客
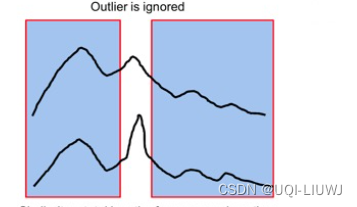
- 优点:对noise不敏感
- 缺点:定义threshold比较困难(这里的threshold指的是,如果两点之间的距离小于这个threshold时,将被视为相同的一个点)
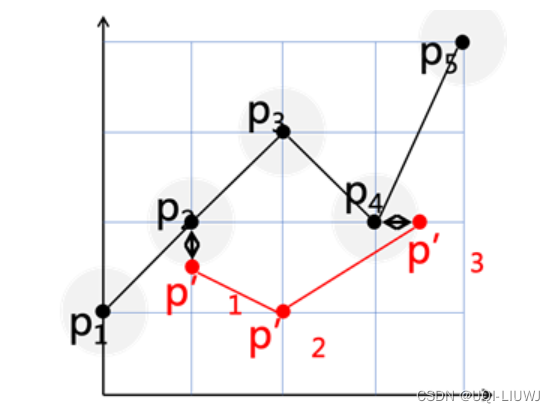
- 比如上图,在这一对threshold的限制下,最长公共弄子序列的长度为2
DIscovering similar multidimensional trajectories, ICDE 2002
1.4 字符串编辑举例EDR
算法笔记:字符串编辑距离(Edit Distance on Real sequence,EDR)/ Levenshtein距离_UQI-LIUWJ的博客-CSDN博客
- 优点:对噪声不敏感
- 缺点:同LCSS,不好界定threshold
''' Robust and fast similarity search formoving object trajectories' SigMod 2005
2 基于形状的距离
2.1 豪斯多夫距离
算法笔记:字符串编辑距离(Edit Distance on Real sequence,EDR)/ Levenshtein距离_UQI-LIUWJ的博客-CSDN博客
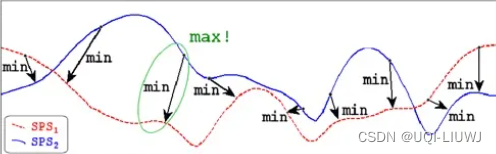
- 缺点:对噪声敏感
The computational geometry of comparing shapes, Efficient algorithms, 2009
2.2 Frechet距离
算法笔记:Frechet距离度量_UQI-LIUWJ的博客-CSDN博客
The computational geometry of comparing shapes, Efficient algorithms, 2009
2.3 上述方法对比
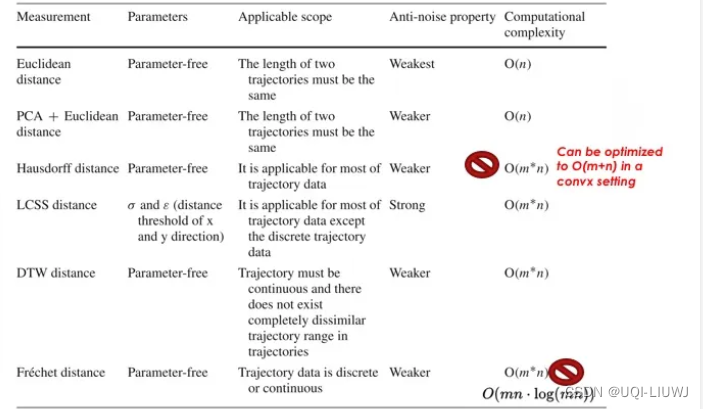
3 基于片段的距离
3.1 One Way Distance
- 轨迹T1到T2的单边轨迹距离
- T1中的点到T2的距离的积分结果,除以T1的距离
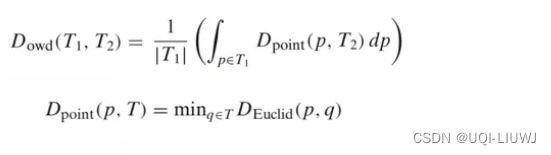
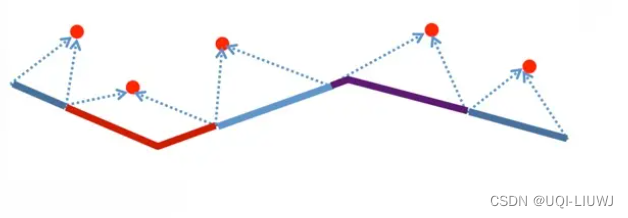
- 轨迹T1和T2的对称双边距离
One way distance: for shape based similarity search of moving object trajectories, Geoinformatica 2008
3.2 多线位置距离(Locality In-between Polylines,LIP)

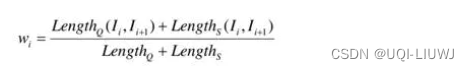
表示两个轨迹的第i个交点,
表示第i个交点和第i+1个交点之间所夹区域的面积
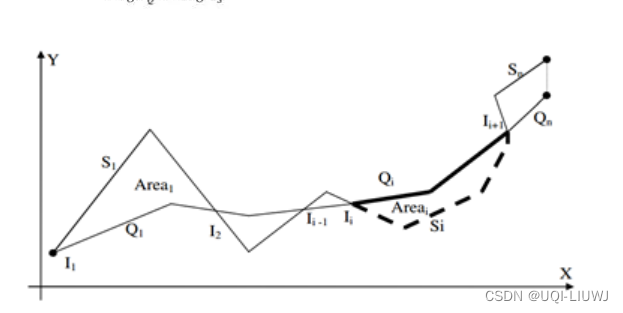
- LIP方法很好理解,当某区域面积的周长占总长比重大时权重也自然就大;
- 当Area均为0时,说明两条轨迹重合没有缝隙,LIP距离为0;
- 当Area加权和大时,则说明两条轨迹之间缝隙较大,LIP距离也就大。
- 此外,权重由区域周长占总长比重的大小而决定,也一定程度对抗了噪音点的干扰。
Similarity search in trajectory databases