【数据结构】快速排序算法你会写几种?

👦个人主页:Weraphael
✍🏻作者简介:目前正在学习c++和算法
✈️专栏:数据结构
🐋 希望大家多多支持,咱一起进步!😁
如果文章有啥瑕疵
希望大佬指点一二
如果文章对你有帮助的话
欢迎 评论💬 点赞👍🏻 收藏 📂 加关注😍
目录
- 一、hoare版本(左右指针法)
- 1.1 算法思想
- 1.2 hoare版本代码实现
- 1.3 hoare版本性能分析
- 二、 基准值选取随机值(优化)
- 三、三数取中(优化)
- 四、小区间优化
- 4.1 思想
- 五、三路划分(优化)
- 六、快速排序之挖坑法
- 6.1 算法思路
- 6.2 代码实现
- 七、前后指针法(最推荐的方法)
- 7.1 算法思路
- 7.2 代码实现
- 八、非递归版快速排序
- 8.1 前言
- 8.2 实现方法
- 8.3 代码实现
一、hoare版本(左右指针法)
1.1 算法思想
【思想】
-
任取待排序元素序列中的某元素作为 基准值
key。一般是第一个元素和最后一个元素。 -
【✨重点】 将待排序集合 分割成两子序列。使得左子序列中所有元素均小于
key,右子序列中所有元素均大于key。
做法:定义两个变量i和j分别指向开头和最后一个元素。请务必记住此结论:如果选取的基准值是第一个元素,要让j先动,反之让i先动。(假设选取的基准值为第一个元素并且要求序列为升序)
若j遇到小于等于 key的数,则停下,然后i开始走,直到i遇到一个大于key的数时,将i和j的内容交换,如果区间内还有元素,则重复以上操作。最后你会发现:i和j最后一定会相遇(可以参考下面动图),此时将相遇点的内容与key交换即可
- 最后左右子序列重复该过程,直到所有元素都排列在相应位置上为止。(递归)
以下是一趟排序的动图演示

在往期博客中,我写了一篇快排算法模板,有兴趣的可以来看看:点击跳转
1.2 hoare版本代码实现
#include <stdio.h>
void Swap(int* x, int* y)
{
int t = *x;
*x = *y;
*y = t;
}
// hoare版本
void quick_sort(int a[], int l, int r)
{
// 如果区间只有一个元素或者没有元素,就没必要排序了
if (l >= r) return;
// 1. 选取一个基准值(以选取第一个元素为例)
int key = a[l];
// 2. 定义i和j,i从左向右走,j从右向左走。
int i = l, j = r;
while (i < j)
{
// 注意:若选择第一个元素作为基准值,则需要j先走;反之让i先走
while (i < j && a[j] >= key) // 找小
{
j--;
}
while (i < j && a[i] <= key) // 找大
{
i++;
}
// 交换
if (i < j)
Swap(&a[i], &a[j]);
}
// 循环结束后,i和j一定会相遇,和基准值交换
Swap(&a[l], &a[i]);
// 3.递归
quick_sort(a, l, i - 1);
quick_sort(a, i + 1, r);
}
【程序结果】

注意:这里会有一个越界 + 死循环问题 + 我犯的错误

- 在
while (i < j && a[j] >= key)循环中,如果不加i < j,那么假设序列已经是升序了,那么就会越界;while (i < j && a[i] <= key)也同理

- 并且如果只写
a[i] < key,将序列中出现数据冗余,就会陷入死循环 - 最后还有一个问题,就是本人初学时犯的(忽略了一个小的知识点qwq)。
与基准值交换Swap(&a[l], &a[i]),不能写成Swap(&key, &a[i])。因为key是一个局部变量,只是存储序列a[l],虽然交换了,但是序列第一个元素并没有改变。我也是通过调试发现的hh
1.3 hoare版本性能分析
- 时间复杂度
快速排序其实是二叉树结构的交换排序方法

递归的高度是logN,而单趟排序基本都要遍历一遍序列,大约有N个数,因此时间复杂度是NlogN
接下来可以和堆排序以及希尔排序来比较一下,它们三者的时间复杂度的量级都是NlogN

我们发现,当数据个数为一百万的时候,快速排序还是非常快的。不愧叫快排
那么快排最坏的情况是什么?
最坏的情况即包括逆序,也包括有序。其时间复杂度是O(N2)

如果数据量大的话,那么栈一定会爆。那如果是这样,快排还叫快排吗?
先说结论:快排的时间复杂度是:O(NlogN)
那么如何解决这个问题呢?通过分析发现,有序和无序就是因为基准值选取的不好。
因此,有人提出了优化基准值可以选取随机值或者三数取中
二、 基准值选取随机值(优化)
做法:使用rand函数随机选取区间中的下标rand() % (r - l),但是这样远远不够,因为递归的时候,左区间会随之改变。因此正确下标取法rand() % (r - l) + l
void quick_sort(int a[], int l, int r)
{
if (l >= r) return;
// 随机选key
// 区间下标范围
int randIdx = (rand() % (r - l)) + l;
Swap(&a[l], &a[randIdx]);
// 以下都和hoare版本一样
int key = a[l];
int i = l, j = r;
while (i < j)
{
while (i < j && a[j] >= key)
{
j--;
}
while (i < j && a[i] <= key)
{
i++;
}
Swap(&a[i], &a[j]);
}
Swap(&a[l], &a[i]);
quick_sort(a, l, i - 1);
quick_sort(a, i + 1, r);
}
【程序结果】
三、三数取中(优化)
- 三数取中是指:第一个元素、最后一个元素和中间元素,选出不是最小也不是最大的那一个(找的是下标)
int GetMinNum(int a[], int l, int r)
{
int mid = (l + r) >> 1;
// 选出不是最大也不是最小的
// 两两比较
if (a[l] < a[mid])
{
if (a[mid] < a[r])
{
return mid;
}
else if (a[r] < a[l])
{
return l;
}
else
{
return r;
}
}
else // a[l] >= a[mid]
{
if (a[l] < a[r])
{
return l;
}
else if (a[r] < a[mid])
{
return mid;
}
else
{
return r;
}
}
}
void quick_sort(int a[], int l, int r)
{
if (l >= r)
return;
// 三数取中
int mid = GetMinNum(a, l, r);
Swap(&a[mid], &a[l]);
// 以下和hoare版本一样
int key = a[l];
int i = l, j = r;
while (i < j)
{
while (i < j && a[j] >= key)
{
j--;
}
while (i < j && a[i] <= key)
{
i++;
}
Swap(&a[i], &a[j]);
}
Swap(&a[l], &a[i]);
quick_sort(a, l, i - 1);
quick_sort(a, i + 1, r);
}
【程序结果】
四、小区间优化
4.1 思想
由于快速排序是基于分治的思想。其实就是二叉树结构的交换排序方法。而我们知道,二叉树最后一层的结点个数是占整个结点个数的一半。并且快排递归到最后每一个都是小区间,但是每一个小区间都需要使用多次递归。这样的消耗确实挺大。
因此我们可以对小区间进行优化,让小区间不要使用递归了,直接使用插入排序来进行优化。因为小区间以及很接近有序了。使用插入排序最佳。当然区间不可以太大,因为我们要考虑小区间直接插入的效率高于递归的效率
那区间的范围在多少合适呢?— 大概在10左右就行
#include <iostream>
using namespace std;
void Swap(int *x, int *y)
{
int t = *x;
*x = *y;
*y = t;
}
int GetMinNum(int a[], int l, int r)
{
int mid = (l + r) >> 1;
// 选出不是最大也不是最小的
// 两两比较
if (a[l] < a[mid])
{
if (a[mid] < a[r])
{
return mid;
}
else if (a[r] < a[l])
{
return l;
}
else
{
return r;
}
}
else // a[l] >= a[mid]
{
if (a[l] < a[r])
{
return l;
}
else if (a[r] < a[mid])
{
return mid;
}
else
{
return r;
}
}
}
void InsertSort(int a[], int n)
{
for (int i = 1; i < n; i++)
{
int end = i - 1;
int tmp = a[i];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + 1] = a[end];
end--;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}
void QuickSort(int a[], int l, int r)
{
if (l >= r)
return;
// 如果区间个数超过10,就使用递归
if ((l - r + 1) > 10)
{
// 三数取中
int mid = GetMinNum(a, l, r);
Swap(&a[mid], &a[l]);
// 以下和hoare版本一样
int key = a[l];
int i = l, j = r;
while (i < j)
{
while (i < j && a[j] >= key)
{
j--;
}
while (i < j && a[i] <= key)
{
i++;
}
Swap(&a[i], &a[j]);
}
Swap(&a[l], &a[i]);
QuickSort(a, l, i - 1);
QuickSort(a, i + 1, r);
}
else
{
InsertSort(a + l, r - l + 1);
}
}
int main()
{
int a[] = {9, 8, 7, 6, 5, 4, 3, 2, 1};
int n = sizeof(a) / sizeof(a[0]);
QuickSort(a, 0, n - 1);
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
return 0;
}
五、三路划分(优化)
这个优化是为了解决大量元素重复的问题,这个博主还未学到。暂且先放放hh
六、快速排序之挖坑法
6.1 算法思路

【算法思路】
- 选取一个基准值并用一个变量保存(这个基值一般是第一个元素或者是最后一个元素),然后序列中基准值这个位置相当于是一个坑等待下一个元素填入
- 如果选取的基准值是第一个元素,老样子
j要从右边向左开始找小,如果找到小,就将j指向的元素填入到坑中,而此时j这个位置是一个坑等待填入;接下来就是i从左向右找大,如果找到了大,就将i指向的元素填入到坑中,同理的,i这个位置是一个坑等待填入 - 最后
i和j相遇,并且一起站着一个坑位hole,然后就把基准值key填入即可 - 递归重复区间
[l, hole - 1]和区间[hole + 1, r]
本质上来说,填坑法和hoare版本类似,相比其更加容易理解
6.2 代码实现
void QuickSort5(int a[], int l, int r)
{
if (l >= r) return;
int x = a[l];
// 如果选择左端点为基准值
// 那么坑位一开始是以基准值为下标
int hole = l;
int i = l, j = r;
while (i < j)
{
while (i < j && a[j] >= x) // 找小
{
j--;
}
// 循环结束后,来到此处说明找到小了
// 将小的填入上一个坑位
// 再更新坑位
a[hole] = a[j];
hole = j;
while (i < j && a[i] <= x)
{
i++;
}
// 和上同理
a[hole] = a[i];
hole = i;
}
// 最后i和j相遇一定会同站一个坑位
// 将基准值填入坑位即可
a[hole] = x;
// 递归
QuickSort5(a, l, hole - 1);
QuickSort5(a, hole + 1, r);
}
七、前后指针法(最推荐的方法)
7.1 算法思路
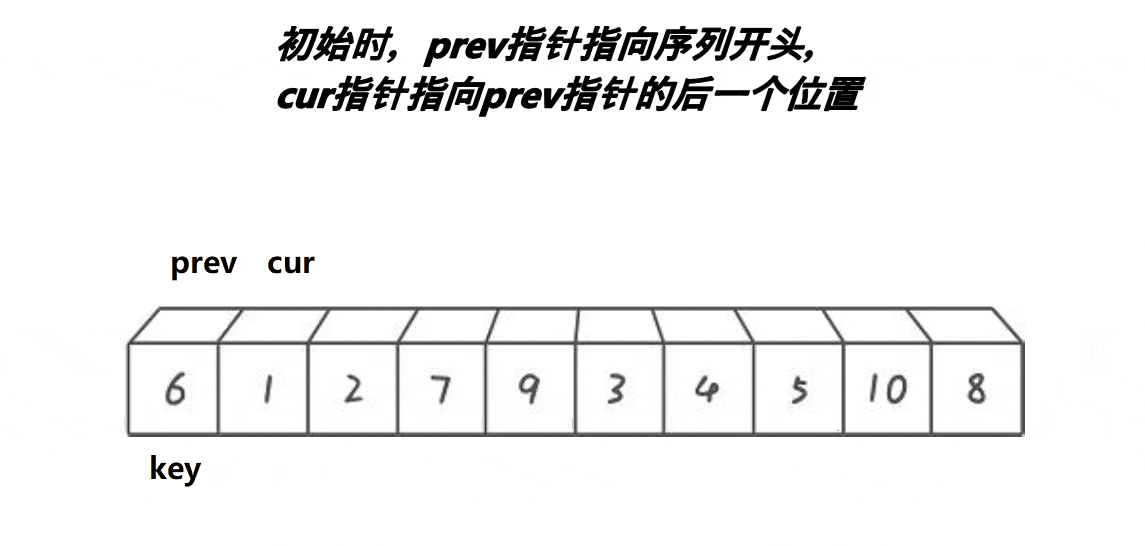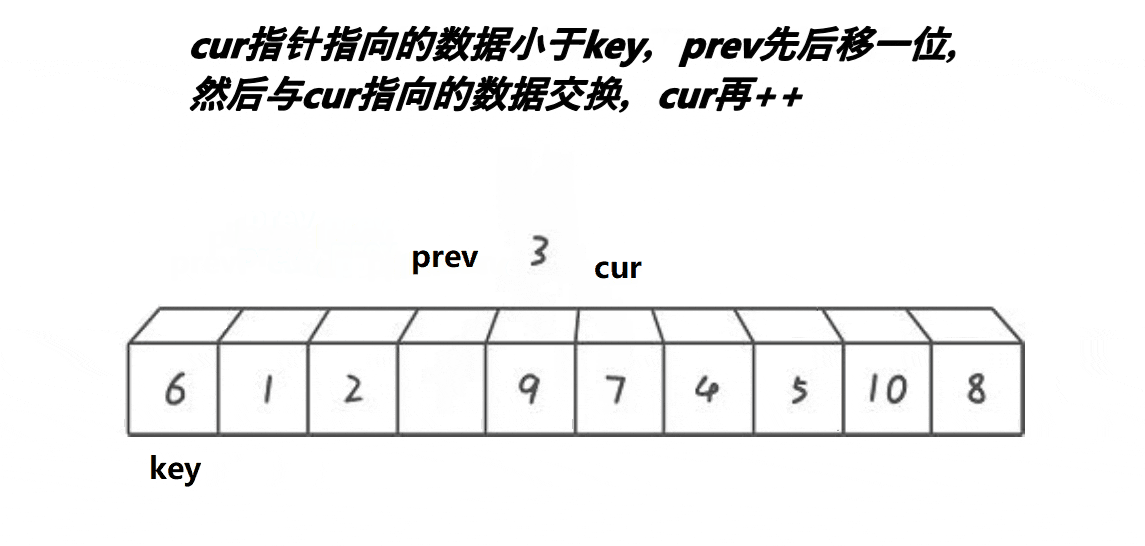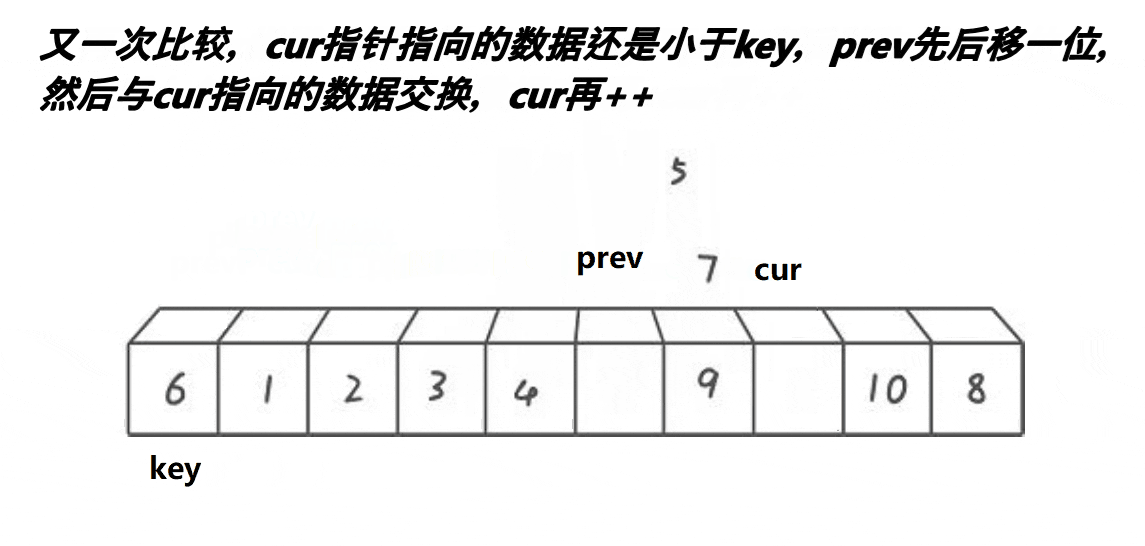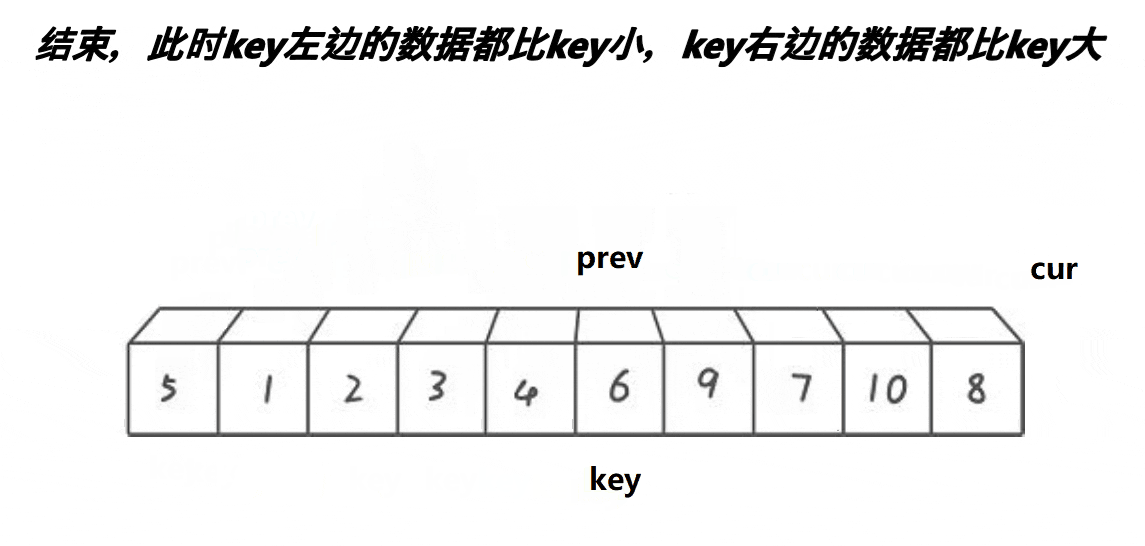
- 选出一个基准值
key,一般是最左边或是最右边的。 - 起始时,
prev指针指向序列开头,cur指针指向prev的下一个位置。 - 若
cur指向的内容小于key,prev先向后移动一位,然后交换prev和cur指针指向的内容,然后cur指针继续向后遍历 - 若
cur指向的内容大于key,则cur指针直接向后遍历。因此可以得出结论,cur本质就是在找小,然后让小的往前靠 - 若
cur超出序列,此时将key和prev指针指向的内容交换即可。
经过一次单趟排序,最终也能使得key左边的数据全部都小于key,key右边的数据全部都大于key。
最后再重复以上操作,直至序列只有一个数据或者序列没有数据时。(递归区间[l, prev - 1]和[prev + 1, r])
7.2 代码实现
void quick_sort(int a[], int l, int r)
{
if (l >= r)
return;
// 1. 选出一个key
int key = a[l];
// 2. 起始时,prev指针指向序列开头,cur指针指向prev+1。
int prev = l, cur = prev + 1;
while (cur <= r)
{
// 3. 若cur指向的内容小于key
// 则prev先向后移动一位,
// 然后交换prev和cur指针指向的内容,
// 然后cur指针++(可以归到第四点)
if (a[cur] < key)
{
++prev;
Swap(&a[prev], &a[cur]);
}
// 4. 若cur指向的内容大于key,则cur指针直接++
++cur;
}
// 若cur到达r + 1位置,此时将key和prev指针指向的内容交换即可。
Swap(&a[l], &a[prev]);
// 递归
quick_sort(a, l, prev - 1);
quick_sort(a, prev + 1, r);
}
八、非递归版快速排序
8.1 前言
我们知道,递归会建立函数栈帧,递归层越深占用栈区的空间就会越大(栈的大小一般是8M或者10M)。当深度足够深时,栈区的空间就会被用完,导致栈溢出。所有最稳妥的方法就是使用非递归。
老实讲,快速排序一般不会发生栈溢出。因为大多数语言的快速排序算法的底层都是使用递归。
那么为啥还需要使用非递归来实现一遍呢?因为往后,如果递归发生栈溢出,就得使用非递归。因此,大家平常可以练习将递归改为非递归;另外,有些面试官为了考察代码能力,偶尔会叫我们手撕一个非递归版快速排序。
8.2 实现方法
快速排序的递归算法主要是在划分子区间,如果要非递归实现快速排序,只需要使用一个栈来维护一个区间即可。注意:要先入右区间,再如左区间。而栈又是先进后出的,因此满足递归是先展开左,再展开右
ps:一般将递归程序改为非递归,首先想到就是栈。因为递归本身就是一个压栈的过程。
更详细的步骤在代码注释里
8.3 代码实现
#include <iostream>
#include <stack>
using namespace std;
int GetMinNum(int a[], int l, int r)
{
int mid = (l + r) >> 1;
// 选出不是最大也不是最小的
// 两两比较
if (a[l] < a[mid])
{
if (a[mid] < a[r])
{
return mid;
}
else if (a[r] < a[l])
{
return l;
}
else
{
return r;
}
}
else // a[l] >= a[mid]
{
if (a[l] < a[r])
{
return l;
}
else if (a[r] < a[mid])
{
return mid;
}
else
{
return r;
}
}
}
void Quick_sort(int a[], int l, int r)
{
// 1. 用栈存储区间
stack<int> st;
// 2. 起始时,区间一定是存在的
// 先入右,再如左
st.push(r);
st.push(l);
// 如果栈不为空,说明还有区间需要排序
while (!st.empty())
{
// 3. 取出区间 (栈顶一定是左区间)
int begin = st.top();
st.pop();
int end = st.top();
st.pop();
// 4. 对取出的区间进行单趟排序
// 以下内容就是三数取中的内容
int mid = GetMinNum(a, begin, end);
swap(a[mid], a[begin]);
int key = a[begin];
int i = begin, j = end;
while (i < j)
{
while (i < j && a[j] >= key)
j--;
while (i < j && a[i] <= key)
i++;
if (i < j)
swap(a[i], a[j]);
}
swap(a[begin], a[i]);
// 5. 更新栈(更新区间)
// [begin,i - 1] [i] [i + 1, end]
// 先让右区间[i + 1, end]入栈
// 如果区间内有数则入栈
// 判断条件写不写等都一样,一个数没必要排序
if (i + 1 < end)
{
st.push(end);
st.push(i + 1);
}
if (begin < i - 1)
{
st.push(i - 1);
st.push(begin);
}
}
}
【程序结果】