机器学习算法——集成学习
目录
- 1. Bagging
1. Bagging
Bagging(bootstrap aggregating:自举汇聚法)也叫装袋法,其思想是通过将许多相互独立的学习器的结果进行结合,从而提高整体学习器的泛化能力,是一种并行集成学习方法。
工作流程
- 从原始样本集中使用Bootstraping(有放回抽样,这种抽样方法产生的样本子集能很好的反映总体的分布特性)方法抽取n个训练样本,共进行K轮抽取,得到K个训练集(训练集之间相互独立)。
- 对于每个训练集,使用相同的数据学习算法(比如决策树、KNN等)独立训练一个基本模型。
- 将测试样例输入到所有基本模型中,每个模型都给出一个预测值。对于分类问题:通过投票的方式确定分类结果(每个模型只有一票);对于回归问题:计算预测值的均值作为预测结果。
代码实践(Jupyter Notebook实现)
from sklearn import neighbors
from sklearn import datasets
from sklearn.ensemble import BaggingClassifier
from sklearn import tree
from sklearn.model_selection import train_test_split
import numpy as np
import matplotlib.pyplot as plt
#------------------------------------------------------------------#
# 使用datasets模块导入鸢尾花数据集,并切分特征值和标签值
# train_test_split(x_data, y_data):将数据集划分为测试集和训练集,
# 默认情况下,训练集占3/4,测试集占1/4
#-----------------------------------------------------------------#
iris = datasets.load_iris()
x_data = iris.data[:,:2]
y_data = iris.target
x_train, x_test, y_train, y_test = train_test_split(x_data, y_data)
# 利用等高线绘制分类边界图
def plot(model):
# 获取数据值所在的范围
x_min, x_max = x_data[:, 0].min() - 1, x_data[:, 0].max() + 1
y_min, y_max = x_data[:, 1].min() - 1, x_data[:, 1].max() + 1
# 生成网格矩阵元素
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
np.arange(y_min, y_max, 0.02))
#-----------------------------------------------------#
# 预测分类结果
# ravel():将多为数据展平为一维数据
# np.c_:按列连接两个数组,即拼接成点的坐标的形式
# contourf(xx, yy, z):创建填充等高线图,参数需为二维数组
#-----------------------------------------------------#
z = model.predict(np.c_[xx.ravel(), yy.ravel()])
z = z.reshape(xx.shape)
cs = plt.contourf(xx, yy, z)
# 创建KNN模型,使用训练集训练模型
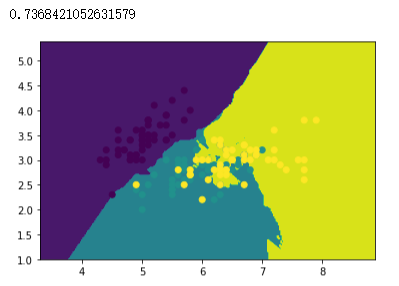
knn = neighbors.KNeighborsClassifier()
knn.fit(x_train, y_train)
# 绘制分类边界图
plot(knn)
# 样本散点图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
# 打印准确率
knn.score(x_test, y_test)
# 创建CART决策树模型,使用训练集训练模型
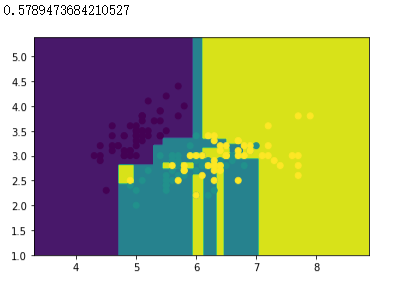
dtree = tree.DecisionTreeClassifier()
dtree.fit(x_train, y_train)
# 绘制分类边界图
plot(dtree)
# 样本散点图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
# 打印准确率
dtree.score(x_test, y_test)
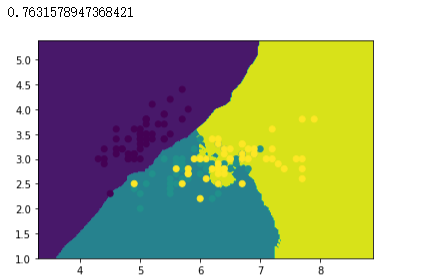
# 创建 Bagging 分类器对象,以KNN分类器作为基分类器,创建100个KNN基分类器
bagging_knn = BaggingClassifier(knn, n_estimators=100)
# 模型拟合
bagging_knn.fit(x_train, y_train)
# 绘制分类边界图
plot(bagging_knn)
# 样本散点图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
# 打印准确率
bagging_knn.score(x_test, y_test)
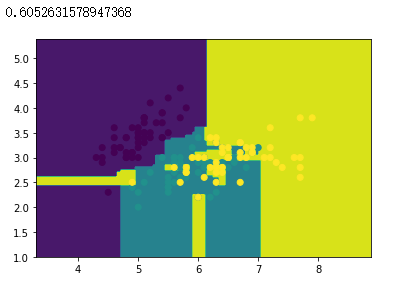
# 创建 Bagging 分类器对象,以CART决策树分类器作为基分类器,创建100个基分类器
bagging_tree = BaggingClassifier(dtree, n_estimators=100)
# 模型拟合
bagging_tree.fit(x_train, y_train)
# 绘制分类边界图
plot(bagging_tree)
# 样本散点图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
# 打印准确率
bagging_tree.score(x_test, y_test)
准确率汇总
| 算法 | 准确率 |
|---|---|
| KNN | 73.6 8% |
| Bagging(KNN) | 76.32% |
| DecisionTree | 57.89% |
| Bagging(DecisionTree) | 60.53% |
注:由于数据集切分的随机性和Bagging中每个基分类器所使用的训练集不同,因此每次运行的结果可能不同,且Bagging的准确率可能会比单分类器的准确率低。
