代码随想录 Day47 动态规划15 LeetCode T583 两个字符串的删除操作 T72 编辑距离
LeetCode T583 两个字符串的删除操作
题目链接:583. 两个字符串的删除操作 - 力扣(LeetCode)

题目思路:
本题有两个思路
1.使用两个字符串的长度之和-2*最长公共子串(换汤不换药)
代码随想录Day45 动态规划13 LeetCode T1143最长公共子序列 T1135 不相交的线 T53最大子数组和-CSDN博客
2.使用不同子序列的思路,从只能删除母串到现在的两个字符串可以相互修改
这里我介绍第二种思路,第一种思路在之前已经介绍过,可以查看我的
1.明确dp数组含义
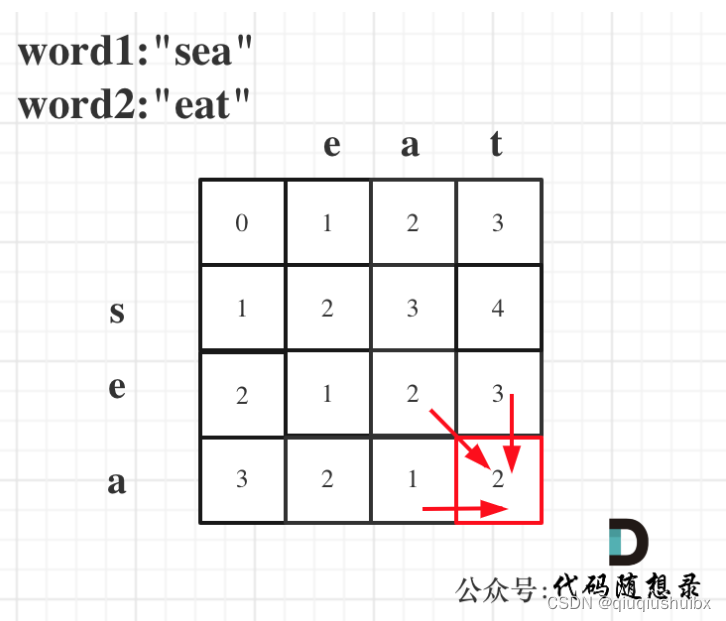
这里的dp数组含义就是以i-1结尾的字符串word1和以j-1为结尾的字符串word2,要想达到相等,所需的最小次数.
2.明确递推公式
分为相等和不相等两种情况
2.1 相等
dp[i][j] = dp[i-1][j-1] 延续这种状态,因为相同无需删除
2.2 不相等
dp[i][j] = min(dp[i][j-1]+1,dp[i-1][j+1],dp[i-1][j-1]+2)
需要删除,这里就选择删除word1的尾字母,删除word2的尾字母或者删除word1和word2的尾字母,求最小值即可
3.初始化dp数组
将dp[i][0] 初始化为i,因为这里word2没有字母,想要相同只能删除word1的全部字母
同理,dp[0][j]初始化为j即可
4.明确遍历顺序
从前向后遍历,因为后面的数据要依托与前面的数据而产生
5.打印dp数组排错
题目代码:
1.最长公共子串法
class Solution {
public int minDistance(String word1, String word2) {
int len1 = word1.length();
int len2 = word2.length();
int[][] dp = new int[len1+1][len2+1];
for(int i = 1;i<=len1;i++){
char c1= word1.charAt(i-1);
for(int j = 1;j<=len2;j++){
char c2 = word2.charAt(j-1);
if(c1 == c2){
dp[i][j] = dp[i-1][j-1] + 1;
}else{
dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);
}
}
}
return len1+len2-2*dp[len1][len2];
}
}
2.删除法
class Solution {
public int minDistance(String word1, String word2) {
int len1 = word1.length();
int len2 = word2.length();
int[][] dp = new int[len1+1][len2+1];
for(int i = 0;i<=len1;i++){
dp[i][0] = i;
}
for(int j = 0;j<=len2;j++){
dp[0][j] = j;
}
for(int i = 1;i<=len1;i++){
char c1= word1.charAt(i-1);
for(int j = 1;j<=len2;j++){
char c2 = word2.charAt(j-1);
if(c1 == c2){
dp[i][j] = dp[i-1][j-1];
}else{
dp[i][j] = Math.min(dp[i-1][j]+1,Math.min(dp[i][j-1]+1,dp[i-1][j-1]+2));
}
}
}
return dp[len1][len2];
}
}LeetCode T72 编辑距离
题目链接:72. 编辑距离 - 力扣(LeetCode)
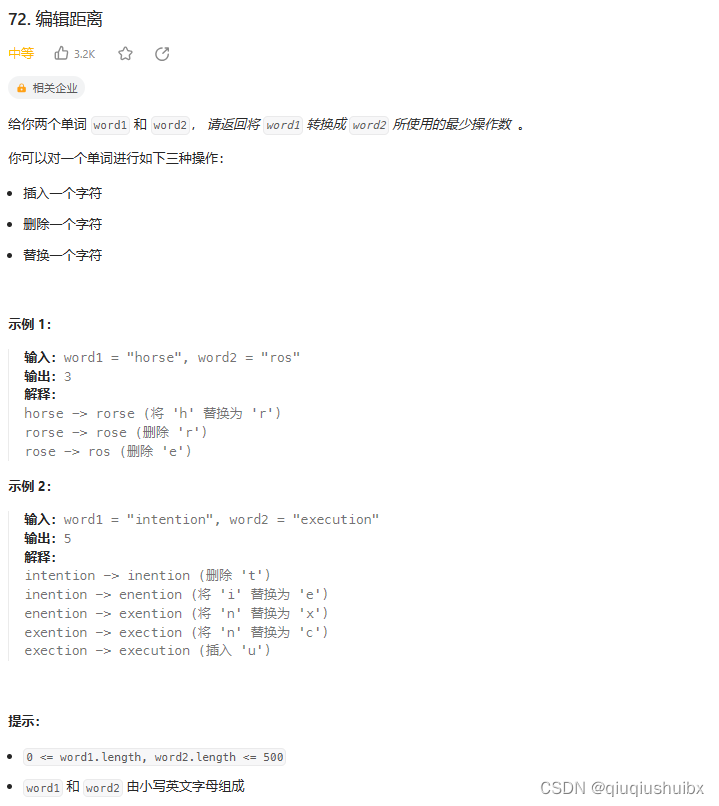
题目思路:
仍然是使用动规五部曲来解决
1.确定dp数组含义
dp[i][j]的含义仍然是以i-1结尾的word1和j-1结尾的word2的最近编辑距离
2.确定递推公式
if (word1[i - 1] == word2[j - 1]) 不操作 if (word1[i - 1] != word2[j - 1]) 增 删 换其实这里的增和删是一样的,比如word1是'ab',word2是'a'
这里我们可以用word1删除一个b或者用word2添加一个b,都是可以的,所以我们考虑以中国情况即可
2.1 相同的情况
如果c1 == c2
那么是不是无需操作直接延续前一次的dp[i-1][j-1]都可以
即dp[i][j] = dp[i-1][j-1];
2.2 不同的情况
这里就要考虑增删改了,其实也可以说是删改即可
能到达dp的就有dp[i-1][j]+1,dp[i][j-1]+1,dp[i-1][j-1]+1(相同直接延续,不同修改一个变成另一个即可)我们在三者之间取最小值即可
3.初始化dp数组
因为dp[i][j]依赖于前面产生,所以我们初始化dp[i][0]和dp[0][j]即可
dp[i][0]其实就是表示i到空字符串需要多少步,当然是i步
同理dp[0][j] = j
4.遍历顺序
从前向后遍历,因为后面的数据依赖前面的数据产生
5.打印dp数组排错
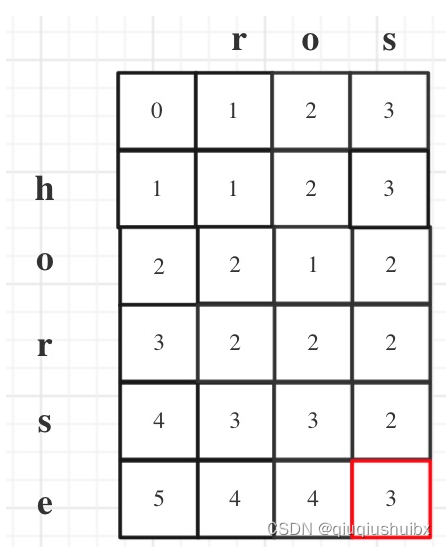
假设word1 = horse
word2 = ros dp数组如下
题目代码:
class Solution {
public int minDistance(String word1, String word2) {
int len1 = word1.length();
int len2 = word2.length();
int[][] dp = new int[len1+1][len2+1];
for(int i = 0;i<=len1;i++){
dp[i][0] = i;
}
for(int j = 0;j<=len2;j++){
dp[0][j] = j;
}
for(int i = 1;i<=len1;i++){
char c1 = word1.charAt(i-1);
for(int j = 1;j<=len2;j++){
char c2 = word2.charAt(j-1);
if(c1 == c2){
dp[i][j] = dp[i-1][j-1];
}else{
dp[i][j] = Math.min(dp[i-1][j-1]+1,Math.min(dp[i-1][j]+1,dp[i][j-1]+1));
}
}
}
return dp[len1][len2];
}
}