【机器学习6】概率图模型
用观测结点表示观测到的数据, 用隐含结点表示潜在的知识, 用边来描述知识与数据的相互关系, 最后基于这样的关系图获得一个概率分布 。
概率图中的节点分为隐含节点和观测节点, 边分为有向边和无向边。 从概率论的角度, 节点对应于随机变量, 边对应于随机变量的依赖或相关关系, 其中有向边表示单向的依赖, 无向边表示相互依赖关系。
概率图模型分为贝叶斯网络(Bayesian Network) 和马尔可夫网络(MarkovNetwork) 两大类。 贝叶斯网络可以用一个有向图结构表示, 马尔可夫网络可以表示成一个无向图的网络结构。 更详细地说, 概率图模型包括了朴素贝叶斯模型、最大熵模型、 隐马尔可夫模型、 条件随机场、主题模型等。
1 贝叶斯网络与马尔科夫网络
1.1 贝叶斯网络

1.2 马尔科夫网络
对于图中所有节点x={x1,x2,…,xn}所构成的一个子集, 如果在这个子集中, 任意两点之间都存在边相连, 则这个子集中的所有节点构成了一个团。 如果在这个子集中加入任意其他节点, 都不能构成一个团, 则称这样的子集构成了一个最大团。

2 朴素贝叶斯模型和最大熵模型
2.1 朴素贝叶斯模型
朴素贝叶斯模型通过预测指定样本属于特定类别的概率P(yi|x)来预测该样本的所属类别:
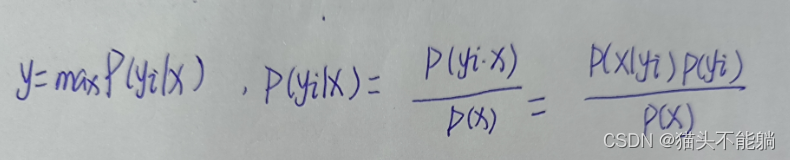
x=(x1,x2,…,xn)为样本对应的特征向量, P(x)为样本的先验概率。 对于特定的样本x和任意类别yi, P(x)的取值均相同, 并不会影响P(yi|x)取值的相对大小, 因此在计算中可以被忽略。 假设特征x1,x2,…,xn相互独立,
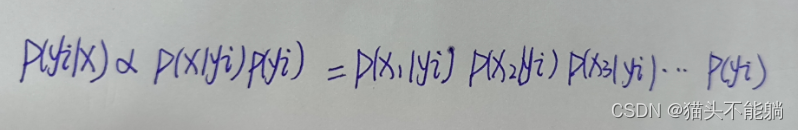
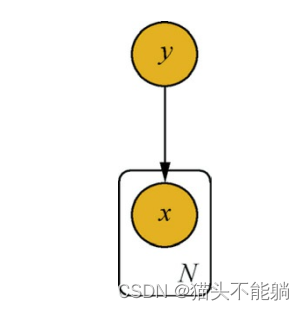
可以看到后验概率P(xj|yi)的取值决定了分类的结果, 并且任意特征xj都由yi的取值所影响。变量y同时对x1,x2,…,xN这N个变量产生影响, 因此概率图模型可以用图表示。
2.2 最大熵模型
最大熵原理是概率模型学习的一个准则, 指导思想是在满足约束条件的模型集合中选取熵最大的模型, 即不确定性最大的模型。
假设离散随机变量x的分布是P(x), 则关于分布P的熵定义为:
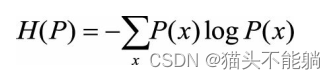
给定离散随机变量x和y上的条件概率分布P(y|x), 定义在条件概率分布上的条件熵为:
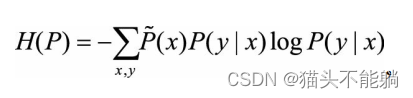
其中 (x)为样本在训练数据集上的经验分布, 即x的各个取值在样本中出现的频率统计.
最大熵模型就是要学习到合适的分布P(y|x), 使得条件熵H§的取值最大。 在对训练数据集一无所知的情况下, 最大熵模型认为P(y|x)是符合均匀分布的。有了训练数据集之后, 特征函数f描述了输入x和输出y之间的一个规律, 例如当x=y时, f(x,y)等于一个比较大的正数。 为了使学习到的模型P(y|x)能够正确捕捉训练数据集中的这一规律(特征) , 我们加入一个约束, 使得特征函数f(x,y)关于经验分布 (x,y)的期望值与关于模型P(y|x)和经验分布 (x)的期望值相等, 即:
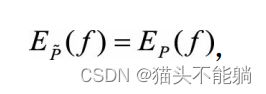
综上, 给定训练数据集 , 以及M个特征函数,最大熵模型的学习等价于约束最优化问题:
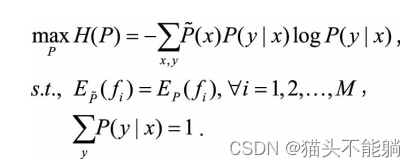
求解之后可以得到最大熵模型的表达形式为:
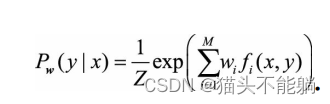
最大熵模型归结为学习最佳的参数w, 使得Pw(y|x)最大化。
P
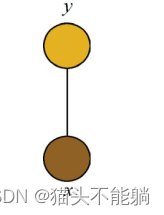
w(y|x)的表达形式非常类似于势函数为指数函数的马尔可夫网络, 其中变量x和y构成了一个最大团:
3生成式模型和判别式模型
假设可观测到的变量集合为X, 需要预测的变量集合为Y, 其他的变量集合为Z。
| 定义 | 代表性模型 | |
|---|---|---|
| 生成式模型 | 对联合概率分布P(X,Y,Z)进行建模, 在给定观测集合X的条件下, 通过计算边缘分布来得到对变量集合Y的推断 | 朴素贝叶斯、贝叶斯网络、 pLSA、 LDA、隐马尔可夫模型等 |
| 判别式模型 | 直接对条件概率分布P(Y,Z/X)进行建模, 然后消掉无关变量Z就可以得到对变量集合Y的预测 | 最大熵模型、最大熵马尔可夫模型、条件随机场 |
4 马尔科夫模型/隐马尔科夫模型/最大熵马尔科夫模型/条件随机场
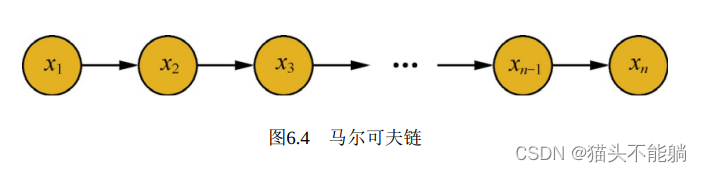
假设一个随机过程中, tn时刻的状态xn的条件分布, 仅仅与其前一个状态xn−1有关, 即P(xn|x1,x2…xn−1)=P(xn|xn−1), 则将其称为马尔可夫过程, 时间和状态的取值都是离散的马尔可夫过程也称为马尔可夫链。
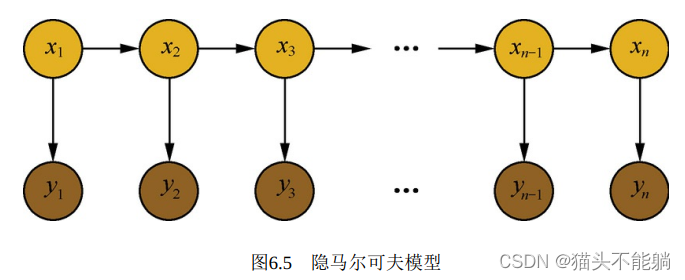
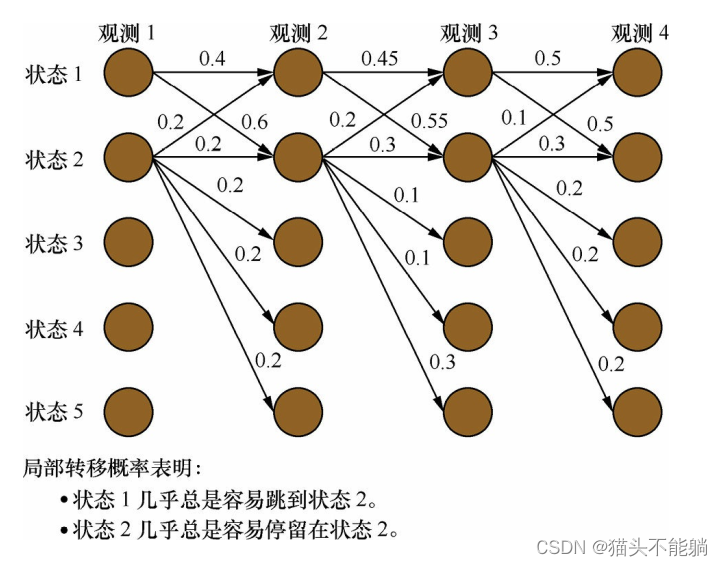
简单的马尔可夫模型中, 所有状态对于观测者都是可见的, 因此在马尔可夫模型中仅仅包括状态间的转移概率。 而在隐马尔可夫模型中, 隐状态xi对于观测者而言是不可见的, 观测者能观测到的只有每个隐状态xi对应的输出yi, 而观测状态yi的概率分布仅仅取决于对应的隐状态xi。 在隐马尔可夫模型中, 参数包括了隐状态间的转移概率、 隐状态到观测状态的输出概率、隐状态x的取值空间、 观测状态y的取值空间以及初始状态的概率分布。
假设有3个不同的葫芦, 每个葫芦里有好药和坏药若干, 现在从3个葫芦中按以下规则倒出药来。
(1) 随机挑选一个葫芦。
(2) 从葫芦里倒出一颗药, 记录是好药还是坏药后将药放回。
(3) 从当前葫芦依照一定的概率转移到下一个葫芦。
(4) 重复步骤(2) 和(3) 。
在整个过程中, 我们并不知道每次拿到的是哪一个葫芦。 用隐马尔可夫模型来描述以上过程, 隐状态就是当前是哪一个葫芦, 隐状态的取值空间为{葫芦1,葫芦2, 葫芦3}, 观测状态的取值空间为{好药, 坏药}, 初始状态的概率分布就是第(1) 步随机挑选葫芦的概率分布, 隐状态间的转移概率就是从当前葫芦转移到下一个葫芦的概率, 而隐状态到观测状态的输出概率就是每个葫芦里好药和坏药的概率。 记录下来的药的顺序就是观测状态的序列, 而每次拿到的葫芦的顺序就是隐状态的序列。
在隐马尔可夫模型中, 假设隐状态(即序列标注问题中的标注) xi的状态满足马尔可夫过程, t时刻的状态xt的条件分布, 仅仅与其前一个状态xt−1有关,即P(xt|x1,x2,…,xt−1)=P(xt|xt−1); 同时隐马尔可夫模型假设观测序列中各个状态仅仅取决于它对应的隐状态P(yt|x1,x2,…,xn,yi,y2,…,yt−1,yt+1,…)=P(yt|xt)。 隐马尔可夫模型建模时考虑了隐状态间的转移概率和隐状态到观测状态的输出概率。实际上, 在序列标注问题中, 隐状态(标注) 不仅和单个观测状态相关, 还和观察序列的长度、 上下文等信息相关。 例如词性标注问题中, 一个词被标注为动词还是名词, 不仅与它本身以及它前一个词的标注有关, 还依赖于上下文中的其他词, 于是引出了最大熵马尔可夫模型。
最大熵马尔可夫模型在建模时, 去除了隐马尔可夫模型中观测状态相互独立的假设, 考虑了整个观测序列, 因此获得了更强的表达能
力。 同时, 隐马尔可夫模型是一种对隐状态序列和观测状态序列的联合概率P(x,y)进行建模的生成式模型, 而最大熵马尔可夫模型是直接对标注的后验概率P(y|x)进行建模的判别式模型。
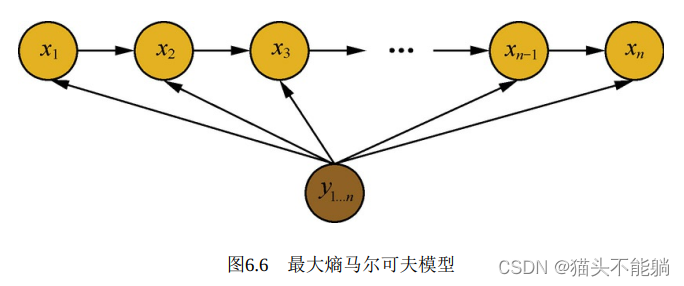
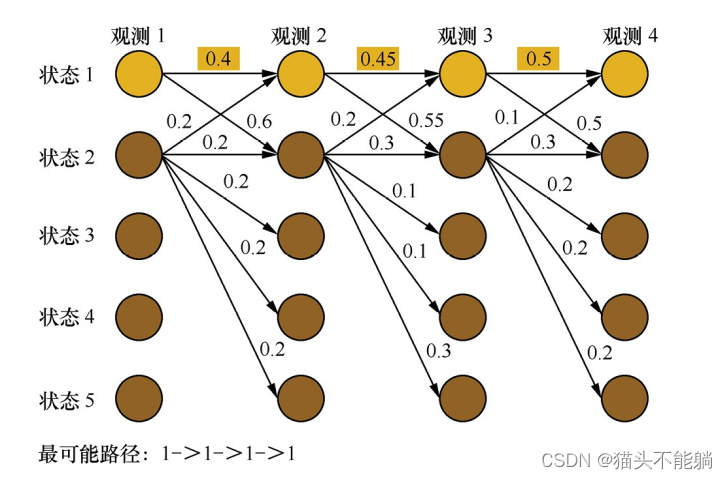
最大熵马尔可夫模型存在标注偏置问题:状态1倾向于转移到状态2, 状态2倾向于转移到状态2本身。 但是实际计算得到的最大概率路径是1->1->1->1, 状态1并没有转移到状态2,这是因为, 从状态2转移出去可能的状态包括1、 2、 3、 4、 5, 概率在可能的状态上分散了,而状态1转移出去的可能状态仅仅为状态1和2, 概率更加集中。
条件随机场(Conditional Random Field, CRF) 在最大熵马尔可夫模型的基础上, 进行了全局归一化,
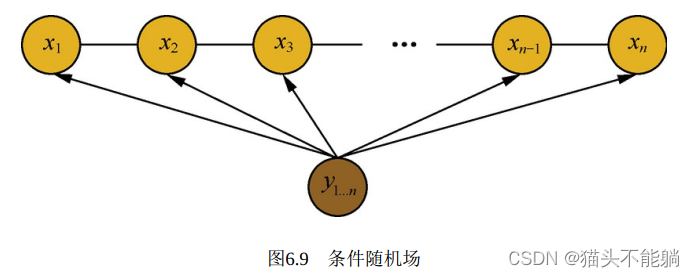
条件随机场建模如下:
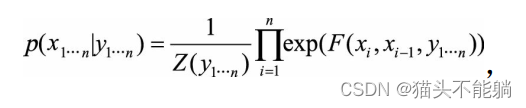
其中归一化因子Z(y1…n)是在全局范围进行归一化, 枚举了整个隐状态序列x1…n的全部可能, 从而解决了局部归一化带来的标注偏置问题。
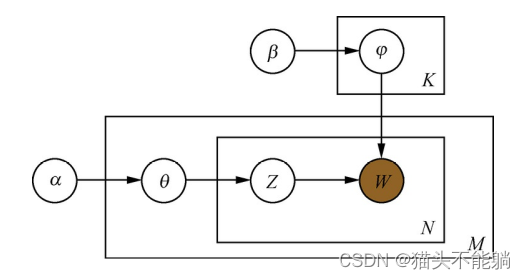
5 主题模型:pLSA(Probabilistic Latent Semantic Analysis) , LDA(Latent DirichletAllocation)
主题模型是一种特殊的概率图模型。 假设有K个主题, 我们就把任意文章表示成一个K维的主题向量, 其中向量的每一维代表一个主题, 权重代表这篇文章属于这个特定主题的概率。 主题模型所解决的事情, 就是从文本库中发现有代表性的主题(得到每个主题上面词的分
布) , 并且计算出每篇文章对应着哪些主题。
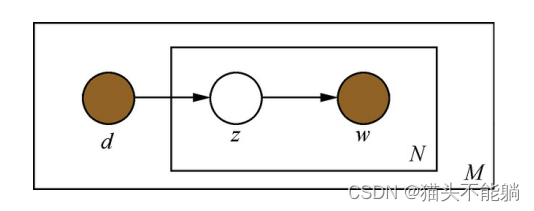
pLSA是用一个生成模型来建模文章的生成过程。 假设有K个主题, M篇文章; 对语料库中的任意文章d, 假设该文章有N个词, 则对于其中的每一个词, 我们首先选择一个主题z, 然后在当前主题的基础上生成一个词w。
LDA可以看作是pLSA的贝叶斯版本, 其文本生成过程与pLSA基本相同, 不同的是为主题分布和词分布分别加了两个狄利克雷(Dirichlet) 先验。 pLSA采用的是频率派思想, 将每篇文章对应的主题分布p(zk|dm)和每个主题对应的词分布p(wn|zk)看成确定的未知常数, 并可以求解出来; 而LDA采用的是贝叶斯学派的思想, 认为待估计的参数(主题分布和词分布) 不再是一个固定的常数, 而是服从一定分布的随机变量。 这个分布符合一定的先验概率分布(即狄利克雷分布) , 并且在观察到样本信息之后, 可以对先验分布进行修正, 从而得到后验分布。