当前位置：首页 > article >正文

K-Means聚类

article 2024/11/14 7:57:09

文章目录

- 概要
- 整体架构流程
- 技术名词解释
- 技术细节
- 小结

概要

K-means聚类算法实现

技术细节

选取的数据集是sklearn.datasets里面的鸢尾花数据集，方便最后的算法评价。

根据手肘法（即根据SSE代价函数）得出最合适的k值。

此处思路是先根据E= $\sum_{i}^{k}\sum\left | x-\bar{x_{i}} \right |^{2}$

定义函数sse，然后在find_k函数中作出sse关于k值变化的点图，得到k=3为最合适的。

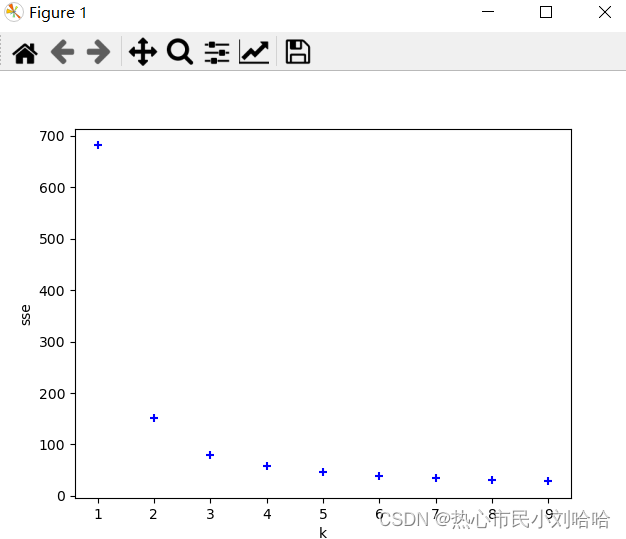
然后为了与后续操作形成更加明显的对比，先作了数据集的两组数据的相关散点图。代码和结果如下：

初始簇中心的选择：

此处随机选择最靠前的K个样本作为初始聚类中心。

因为是分为三簇，此处的思想是先利用cdist()函数计算各样本点到上一次迭代的聚类中心的距离，根据各点对应的距离最小值得到各样本点所在的簇。将各簇存在同一个列表中进行存储。并利用list的sum（）函数除以列表长度计算聚类中心的坐标。最终返回分类后的各簇情况和聚类中心组成的列表。

每次迭代classification函数都是一次簇的更新运算。

后面的代码利用了迭代的方式，如果得到的聚类中心与上一次的聚类中心不同就对数据对象进行重新分配，最终得到最后的聚类中心和聚类情况。

输出结果：

此处的思想是直接读取迭代结束后返回的存放聚类情况的列表a，分别用不同的点的样式表示各簇数据，并将最后的三个聚类中心标出，最终可视化得到如下图。

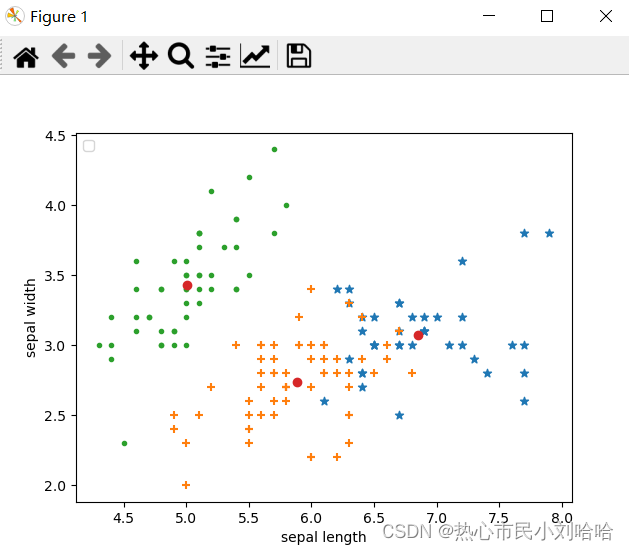
代码

import matplotlib.pyplot as plt
import numpy as np
from sklearn.cluster import KMeans
from sklearn.datasets import load_iris
from scipy.spatial.distance import cdist
iris = load_iris()
X = iris.data[:]
def sse(k,X):#代价函数
    x=0
    km=KMeans(n_clusters=k)
    km.fit(X)
    d=cdist(X,km.cluster_centers_)
    for i in d:
        x+=min(i)**2
    return x
def find_k(X):
    #绘图
    y=[]
    k=np.arange(1,10)
    for i in k:
        y.append(sse(i,X))
    plt.scatter(k, y, c = "blue", marker='+', label='label2')
    plt.xlabel('k')
    plt.ylabel('sse')
    plt.show()
def show(X):
    # 取其中两个维度，绘制原始数据散点分布图
    # x, y为散点坐标，c是散点颜色，marker是散点样式（如'o'为实心圆）
    x=[]
    y=[]
    for i in X:
        x.append(i[0])
        y.append(i[1])
    plt.scatter(x,y)#可视化一组数据
    # 横坐标轴标签
    plt.xlabel('sepal length')
    # 纵坐标轴标签
    plt.ylabel('sepal width')
    # plt.legend设置图例的位置
    plt.legend(loc=2)
    plt.show()
# print(iris)
def center(X,k):#随机选取聚类中心
    l=[]
    for i in range(k):
        l.append(list(X[i]))
    return l
def classification(X,l):
    a=[[],[],[]]
    b=[]
    d=cdist(X,l)
    for i in range(len(d)):
        for j in range(len(l)):
            if d[i][j]==min(d[i]):
                a[j].append(X[i])
    for i in range(len(a)):
        b.append(list(sum(a[i])/len(a[i])))
    return a,b#以l为聚类中心分类后的a和新聚类中心b
find_k(X)#根据SSE和K的关系，选择k=3
show(X)
l=center(X,3)
a,b=classification(X,l)
while True:
    if l==b:
        break
    l=b
    a,b=classification(X,l)
print(b)
# 取其中两个维度，绘制聚类后散点分布图
# x, y为散点坐标，c是散点颜色，marker是散点样式（如'o'为实心圆）
x=[]
y=[]
for j in a[0]:
    x.append(j[0])
    y.append(j[1])
plt.scatter(x,y,marker='*')#可视化一组数据
x=[]
y=[]
for j in a[1]:
    x.append(j[0])
    y.append(j[1])
plt.scatter(x,y,marker='+')#可视化一组数据
x=[]
y=[]
for j in a[2]:
    x.append(j[0])
    y.append(j[1])
plt.scatter(x,y,marker='.')#可视化一组数据
x=[]
y=[]
for j in b:
    x.append(j[0])
    y.append(j[1])
plt.scatter(x,y,marker='o')#可视化一组数据
    # 横坐标轴标签
plt.xlabel('sepal length')
    # 纵坐标轴标签
plt.ylabel('sepal width')
    # plt.legend设置图例的位置
plt.legend(loc=2)
plt.show()