整形数据和浮点型数据在内存中的存储差别
愿所有美好如期而遇

我们先来看代码,猜猜结果是什么呢?
int main()
{
//以整型数据的方式存储
int n = 10;
float* m = (float*)&n;
//以整型数据的方式读取
printf("%d\n", n);
//以浮点型数据的方式2读取
printf("%f\n", *m);
printf("----------------------------\n");
//以浮点型数据的方式存储
*m = 10.0;
//以整型数据的方式读取
printf("%d\n", n);
//以浮点型数据的方式读取
printf("%f\n", *m);
return 0;
}
你是不是觉得答案是10 10.0 10 10.0 呢?
那么我们接下来解释一下为什么是上面那个结果
首先,整型数据和浮点型数据在内存中的存储方式是不同的
(1)整型数据的存储方式是怎样的呢?
在看下面的解释前,如果看不懂请参考:原码,反码,补码,char大小范围的解释
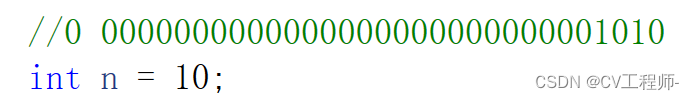
整型数据在内存中直接转换为二进制后以补码形式存储。
(2)浮点型数据的存储方式是怎样的呢?
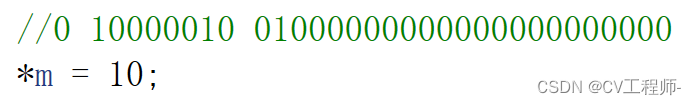
我们要对他的二进制分三部分去看,符号位,指数位,有效数字位(已经用空格分开)
10.0我们可以写成(-1)^0 *1.010* 2^3,(-1)^0,0就是符号位,正数为0,负数为1,1.010就是我们的有效数字,2^3,3就是我们的指数,但是float类型的数据指数在存储时需要加上127,double类型的数据指数在存储时要加上1023,这是IEE754的规定。
而且他还规定了float的指数位有8位,有效数字位23,double指数位有11位,有效数字位52位。数位为unsigned int类型,恒为正数。
指数为3 + 127 ,也就是130,转换为二进制也就是10000010,而有效数字位不存储1,在读取数据时自动前面补1,这样就节省了一位去存储有效数字,也就提高了精度。
读取数据时如何读取?分三种情况:
一:指数位不是全0也不是全1
好比我们上面的10的二进制,我们读取时如何读取?
先看符号位,是正数,然后看指数位,指数位减去127,也就剩下3,也就是2^3,再看有效数字位,0100...,也就是1.0100......,最后我们乘起来:(-1)^0 * 2^3 * 1.010...
二:指数位全是0
那也就相当于我们原来的指数是-127,加上127后为0,那么指数位就是2^-127,这时,我们在读取时就丢掉有效数字位本来会加的那个1,直接用符号位乘指数以及后面的有效数字位。
三:指数位全是1
也就相当于是128+127,我们原本的指数位就是128,也就是2^128,表示一个非常大的数据。
