OpenCV快速入门：直方图、掩膜、模板匹配和霍夫检测

前言

在数字图像处理领域，直方图、掩膜技术、模板匹配以及霍夫变换是不可或缺的工具。本文将简要介绍这些基础概念和技术在OpenCV中的应用。通过对本篇文章的学习，我们将获得对直方图分析、图像优化、模板匹配和霍夫检测等关键概念的基本理解。

一、直方图基础

数字图像处理中，直方图是一项关键工具，能够帮助我们理解图像的分布特征并进行有效的图像增强。在本节中，我们将深入研究直方图的基础知识，并使用OpenCV展示其生成、归一化、均衡化等基本操作。

1.1 直方图的概念和作用

直方图是图像处理中用于表示图像像素强度分布的一种工具。它是通过统计图像中每个强度值（灰度级别）的像素数量来生成的。直方图可以帮助我们了解图像的整体特征，包括亮度和对比度的分布情况。

下面演示如何使用OpenCV和Matplotlib（如果可用）来计算和绘制示例图像的直方图。

import cv2
import numpy as np

# 尝试导入Matplotlib
try:
    import matplotlib.pyplot as plt
    use_matplotlib = True
except ImportError:
    use_matplotlib = False

# 读取图像
image = cv2.imread('tulips.jpg', cv2.IMREAD_GRAYSCALE)

# 计算直方图
hist = cv2.calcHist([image], [0], None, [256], [0, 256])

# 绘制直方图
if use_matplotlib:
    # 使用Matplotlib绘制直方图
    plt.plot(hist)
    plt.title('Histogram')
    plt.xlabel('Pixel Value')
    plt.ylabel('Frequency')
    plt.show()
else:
    print("Matplotlib未安装！")
    print("直方图统计信息:")
    # 打印统计数据
    print(f'最小值: {np.min(image)}')
    print(f'最大值: {np.max(image)}')
    print(f'平均值: {np.mean(image)}')
    print(f'中位数: {np.median(image)}')

    # 计算众数
    mode = np.argmax(hist)
    print(f'众数: {mode}')

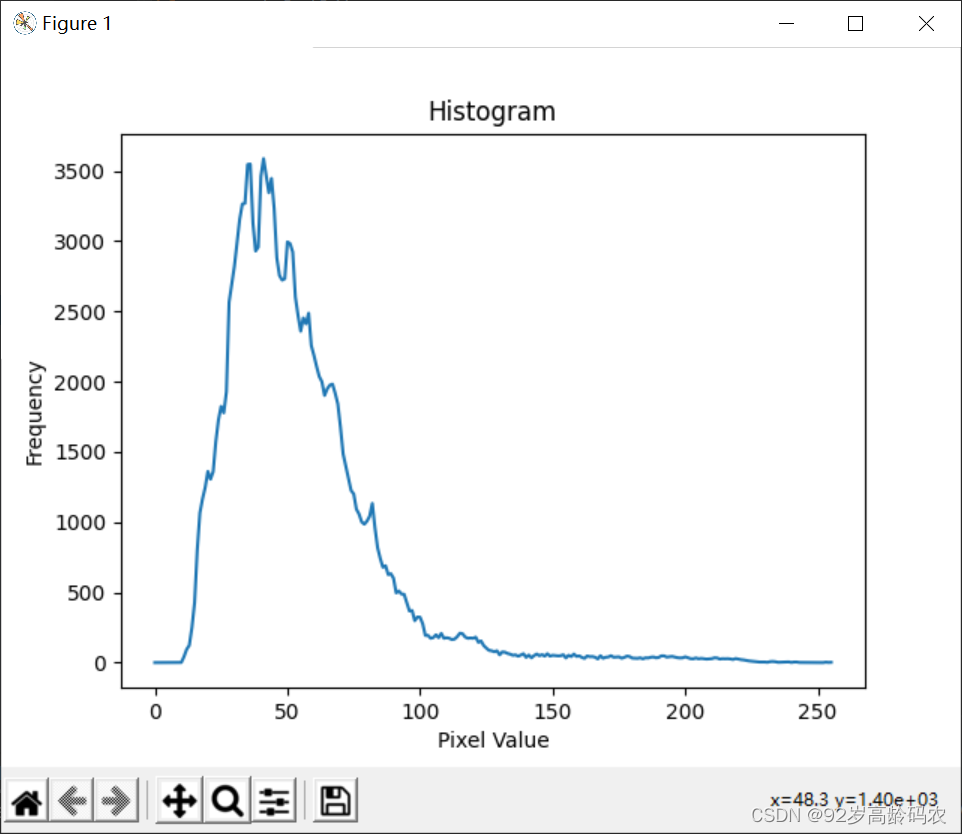
以下是代码的详细描述：

1. 导入库：

   • cv2：OpenCV库，用于图像处理。
   • numpy：用于科学计算。
   • matplotlib.pyplot：用于绘制图表。

2. 读取图像：

   • 使用cv2.imread读取名为 ‘tulips.jpg’ 的图像，以灰度模式加载。

3. 计算直方图：

   • 使用cv2.calcHist计算图像的直方图。
   • 第一个参数是图像。
   • 第二个参数是通道索引，因为这是灰度图像，所以通道索引为[0]。
   • 第三个参数为掩码，这里为None，表示对整个图像进行统计。
   • 第四个参数是直方图的大小，这里为256，表示256个灰度级别。
   • 第五个参数是灰度级别的范围，这里是[0, 256]。

4. 绘制直方图：

   • 如果Matplotlib可用，则使用Matplotlib绘制直方图。
   • 否则，打印一些基本的统计信息，如最小值、最大值、平均值、中位数和众数。

5. Matplotlib可用性检查：

   • 尝试导入Matplotlib，如果成功则设置use_matplotlib为True，否则为False。

6. 绘制直方图（Matplotlib可用时）：

   • 使用Matplotlib的plt.plot函数绘制直方图。
   • 添加标题、X轴和Y轴标签。

这段代码通过直方图提供了对图像像素强度分布的可视化和统计信息，帮助了解图像的整体特征。

1.2 使用OpenCV生成直方图

在没有Matplotlib包的情况下，可以使用OpenCV来生成直方图。

首先，导入必要的库：

import cv2
import numpy as np

然后，定义一个鼠标移动的回调函数，用于获取鼠标位置并在图像右上角显示对应的直方图值：

def on_mouse_move(event, x, y, flags, param):
    global combined_image
    if event == cv2.EVENT_MOUSEMOVE:
        # 计算对应的直方图值
        index = x - O_x
        if 0 <= index < 256:
            hist_value = int(hist[index])
            # 在图像右上角显示绿色的值
            value_text = f'x={index}, y={hist_value}'
            hist_image_copy = cv2.putText(combined_image.copy(), value_text, (O_x + 100, 20),
                                          cv2.FONT_HERSHEY_SIMPLEX, 0.6, (0, 255, 0), 2)
            cv2.imshow('Histogram', hist_image_copy)

接着，读取图像并计算直方图：

image = cv2.imread('tulips.jpg', cv2.IMREAD_GRAYSCALE)
hist = cv2.calcHist([image], [0], None, [256], [0, 256])

创建一个空白图像作为画布：

hist_image = np.zeros((300, 300, 3), dtype=np.uint8)

归一化直方图，并设置坐标原点：

hist_normalized = cv2.normalize(hist, None, 0, 255, cv2.NORM_MINMAX)
O_x = 20
O_y = 280

画坐标轴、标出最大值，并将归一化后的直方图绘制在画布上：

# 画坐标轴
cv2.line(hist_image, (O_x, O_y), (O_x + 255, O_y), (150, 150, 150), 1)
cv2.line(hist_image, (O_x, O_y), (O_x, O_y - 255), (150, 150, 150), 1)

# 标出最大值
max_value = int(max(hist))
cv2.putText(hist_image, str(max_value), (O_x - 10, 20), cv2.FONT_HERSHEY_SIMPLEX, 0.6, (255, 255, 255), 2)

# 将直方图绘制在画布上
for i in range(1, 256):
    point_start = tuple((i - 1 + O_x, O_y - int(hist_normalized[i - 1])))
    point_end = tuple((i + O_x, O_y - int(hist_normalized[i])))
    cv2.line(hist_image, point_start, point_end, (255, 200, 0), 1)

调整原图的大小，并在画布右侧拼接原图：

image_resized = cv2.resize(image, (300, 300))
image_resized = cv2.merge([image_resized, image_resized, image_resized])
combined_image = cv2.hconcat([hist_image, image_resized])

最后，显示拼接后的图像，并设置鼠标回调函数：

cv2.imshow('Histogram', combined_image)
cv2.setMouseCallback('Histogram', on_mouse_move)
cv2.waitKey(0)
cv2.destroyAllWindows()

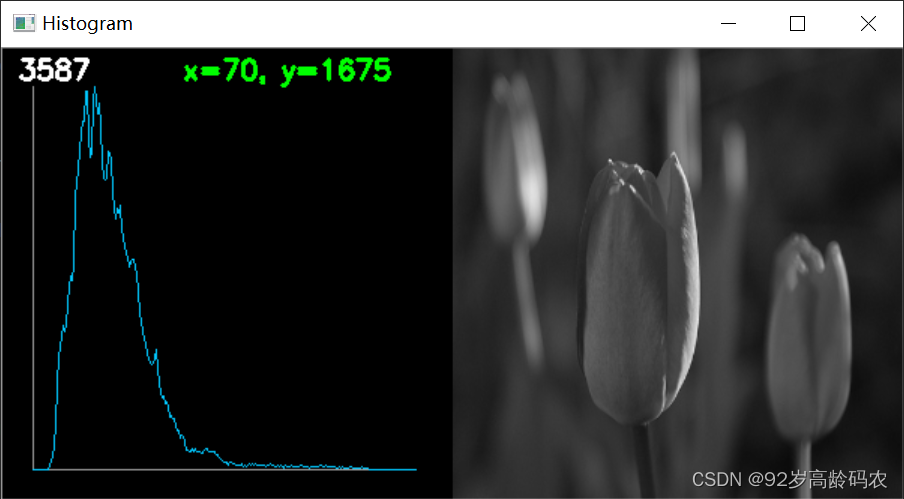
这段代码通过OpenCV生成并显示了图像的直方图，同时在图像右上角动态显示鼠标位置对应的直方图值，帮助用户更直观地理解图像的像素分布情况。

以下是一个完整代码示例：

import cv2
import numpy as np


# 回调函数，用于获取鼠标移动的位置并在图像右上角显示对应的值
def on_mouse_move(event, x, y, flags, param):
    global combined_image
    if event == cv2.EVENT_MOUSEMOVE:
        # 计算对应的直方图值
        index = x - O_x
        if 0 <= index < 256:
            hist_value = int(hist[index])
            # 在图像右上角显示绿色的值
            value_text = f'x={index}, y={hist_value}'
            hist_image_copy = cv2.putText(combined_image.copy(), value_text, (O_x + 100, 20),
                                          cv2.FONT_HERSHEY_SIMPLEX, 0.6, (0, 255, 0), 2)
            cv2.imshow('Histogram', hist_image_copy)


# 读取图像
image = cv2.imread('tulips.jpg', cv2.IMREAD_GRAYSCALE)
# 计算直方图
hist = cv2.calcHist([image], [0], None, [256], [0, 256])

# 创建一张空白图像作为画布
hist_image = np.zeros((300, 300, 3), dtype=np.uint8)

# 归一化直方图
hist_normalized = cv2.normalize(hist, None, 0, 255, cv2.NORM_MINMAX)

# 坐标原点
O_x = 20
O_y = 280

# 画坐标轴
cv2.line(hist_image, (O_x, O_y), (O_x + 255, O_y), (150, 150, 150), 1)
cv2.line(hist_image, (O_x, O_y), (O_x, O_y - 255), (150, 150, 150), 1)

# 标出最大值
max_value = int(max(hist))
cv2.putText(hist_image, str(max_value), (O_x - 10, 20), cv2.FONT_HERSHEY_SIMPLEX, 0.6, (255, 255, 255), 2)

# 将直方图绘制在画布上
for i in range(1, 256):
    point_start = tuple((i - 1 + O_x, O_y - int(hist_normalized[i - 1])))
    point_end = tuple((i + O_x, O_y - int(hist_normalized[i])))
    cv2.line(hist_image, point_start, point_end, (255, 200, 0), 1)

# 调整原图的高度与画布相同
image_resized = cv2.resize(image, (300, 300))
image_resized = cv2.merge([image_resized, image_resized, image_resized])
# 在画布左侧拼接原图
combined_image = cv2.hconcat([hist_image,image_resized ])

# 显示拼接后的图像
cv2.imshow('Histogram', combined_image)

# 设置鼠标回调函数
cv2.setMouseCallback('Histogram', on_mouse_move)

cv2.waitKey(0)
cv2.destroyAllWindows()

1.3 直方图归一化

直方图归一化是图像处理中一项重要的操作，它通过调整直方图的尺度，使其能够更好地比较不同图像的像素强度分布。这一步骤通常在直方图分析和图像匹配中广泛应用。

1.3.1 直方图归一化原理

直方图归一化的原理在于将直方图中的频率值归一到特定的范围，通常是$[0,1]$。这样做的目的是消除不同图像大小和灰度级别的影响，使得它们在相同的标准下进行比较。

1.3.2 直方图归一化公式

直方图归一化的数学表达式如下：

$$P(i)=\frac{H(i)}{N}$$

其中：

• $P(i)$ 是归一化后的直方图值；
• $H(i)$ 是原始直方图中的频率值；
• $N$ 是图像的总像素数。

1.3.3 直方图归一化代码示例

使用OpenCV进行直方图归一化的代码示例如下：

import cv2
import matplotlib.pyplot as plt

# 读取图像
image = cv2.imread('image.jpg', cv2.IMREAD_GRAYSCALE)

# 计算直方图
hist = cv2.calcHist([image], [0], None, [256], [0, 256])

# 归一化直方图
normalized_hist = hist / (image.shape[0] * image.shape[1])

# 绘制原始直方图
plt.subplot(2, 1, 1)
plt.plot(hist)
plt.title('Original Histogram')
plt.xlabel('Pixel Value')
plt.ylabel('Frequency')

# 绘制归一化后的直方图
plt.subplot(2, 1, 2)
plt.plot(normalized_hist)
plt.title('Normalized Histogram')
plt.xlabel('Pixel Value')
plt.ylabel('Normalized Frequency')

plt.tight_layout()
plt.show()

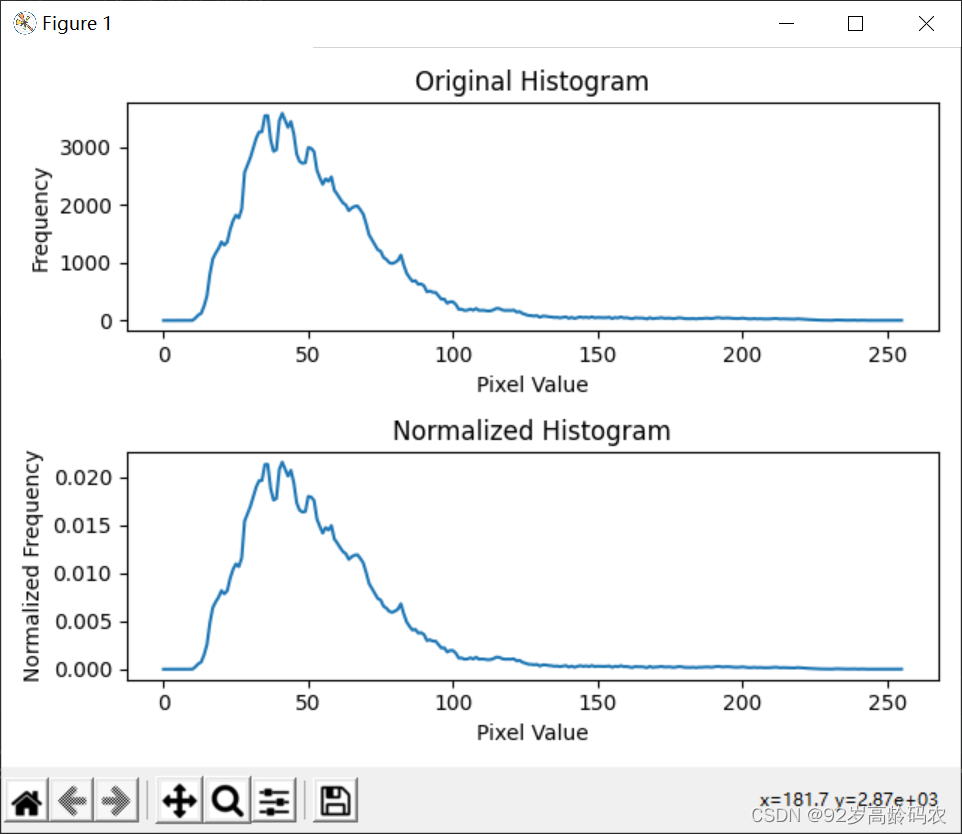
在这个示例中，我们首先计算了原始直方图，然后通过除以图像的总像素数来归一化直方图。最终，通过matplotlib库绘制了原始直方图和归一化后的直方图，使得它们可以进行直观的比较。

直方图归一化是图像处理中一个有用的预处理步骤，有助于确保不同图像在进一步分析和处理中具有可比性。

1.3.4 OpenCV内置方法：normalize()

OpenCV提供了内置的normalize()方法，方便我们对直方图进行归一化处理。

1.3.4.1 normalize()方法介绍

OpenCV的normalize()方法是一个功能强大的函数，用于将数组归一化到指定的范围内。对于直方图，我们可以使用这个方法将其归一化到$[0,1]$范围，以便更好地比较不同图像的像素强度分布。

# 归一化直方图
hist_normalized = cv2.normalize(hist, None, 0, 1, cv2.NORM_MINMAX)

1.3.4.2 normalize()方法参数解释

在上述代码中，normalize()方法的参数解释如下：

• hist: 待归一化的数组，这里是直方图。
• None: 如果指定了目标数组，则归一化结果会被存储在这里。由于我们只需得到归一化后的直方图，因此传入None。
• 0, 1: 归一化的目标范围，这里是$0,1$。
• cv2.NORM_MINMAX: 归一化的类型，表示按照最小值和最大值进行归一化。

此外，OpenCV还提供了其他归一化的类型，如NORM_HAMMING、NORM_L1、NORM_L2等，根据实际需求选择合适的类型。

1.3.4.3 代码示例

下面是一个完整的代码示例，演示了如何使用normalize()方法对直方图进行归一化：

import cv2
import matplotlib.pyplot as plt

# 读取图像
image = cv2.imread('image.jpg', cv2.IMREAD_GRAYSCALE)

# 计算直方图
hist = cv2.calcHist([image], [0], None, [256], [0, 256])

# 使用normalize()方法归一化直方图
hist_normalized = cv2.normalize(hist, None, 0, 1, cv2.NORM_MINMAX)

# 绘制原始直方图
plt.subplot(2, 1, 1)
plt.plot(hist)
plt.title('Original Histogram')
plt.xlabel('Pixel Value')
plt.ylabel('Frequency')

# 绘制归一化后的直方图
plt.subplot(2, 1, 2)
plt.plot(hist_normalized)
plt.title('Normalized Histogram')
plt.xlabel('Pixel Value')
plt.ylabel('Normalized Frequency')

plt.tight_layout()
plt.show()

通过这个示例，我们展示了normalize()方法的简便用法，并对比了原始直方图和归一化后的直方图，以便更好地理解直方图归一化的作用。

在实际图像处理中，选择适当的归一化方法可以帮助我们更准确地比较和分析不同图像的特征。normalize()方法的灵活性和便捷性使其成为处理直方图的理想选择。

1.4 直方图均衡化

直方图均衡化通过调整像素强度分布，使图像的对比度得到增强，从而提升图像的视觉质量。

1.4.1 直方图均衡化原理

直方图均衡化的核心思想是将图像的灰度级分布拉伸到更广泛的范围内。通过对图像中的亮度值进行重新分配，使得整个灰度范围内的像素值都得到了充分利用，增强了图像的对比度。

1.4.2 直方图均衡化公式

直方图均衡化的数学表达式如下：

$$G(i)=\frac{T(i)-T_{\text{min}}}{N-1}\times (L-1)$$

其中：

• $G(i)$ 是均衡化后的灰度级；
• $T(i)$ 是原始直方图的累积分布函数；
• $T_{\text{min}}$ 是原始直方图的最小非零累积值；
• $N$ 是图像的总像素数；
• $L$ 是图像的灰度级数。

1.4.3 直方图均衡化代码示例

下面是使用OpenCV进行直方图均衡化的代码示例：

import cv2

# 读取图像
image = cv2.imread('tulips.jpg')

# 分离通道
channels = cv2.split(image)

# 对每个通道进行均衡化
equalized_channels = [cv2.equalizeHist(channel) for channel in channels]
equalized_image = cv2.merge(equalized_channels)
# 显示原图和均衡化后的图像
cv2.imshow('Equalized Image', cv2.hconcat([image, equalized_image]))
cv2.waitKey(0)
cv2.destroyAllWindows()

import matplotlib.pyplot as plt

# 创建Matplotlib子图
fig, axes = plt.subplots(2, 4, figsize=(12, 8))
FONT_SIZE = 10
# 显示原图的直方图
axes[0, 0].hist(image.ravel(), bins=256, color='gray', alpha=0.7)
axes[0, 0].set_title('Original Image Histogram', fontsize=FONT_SIZE)
axes[0, 0].set_xlabel('Pixel Value', fontsize=FONT_SIZE)
axes[0, 0].set_ylabel('Frequency', fontsize=FONT_SIZE)

# 显示原图的通道直方图
for i, color in enumerate(['Blue', 'Green', 'Red']):
    axes[0, i + 1].hist(channels[i].ravel(), bins=256, color=color.lower(), alpha=0.7)
    axes[0, i + 1].set_title(f'Original {color} Channel Histogram', fontsize=FONT_SIZE)
    axes[0, i + 1].set_xlabel('Pixel Value', fontsize=FONT_SIZE)
    axes[0, i + 1].set_ylabel('Frequency', fontsize=FONT_SIZE)

# 显示均衡化后的直方图
axes[1, 0].hist(equalized_image.ravel(), bins=256, color='gray', alpha=0.7)
axes[1, 0].set_title('Equalized Image Histogram', fontsize=FONT_SIZE)
axes[1, 0].set_xlabel('Pixel Value', fontsize=FONT_SIZE)
axes[1, 0].set_ylabel('Frequency', fontsize=FONT_SIZE)

# 显示均衡化后的通道直方图
for i, color in enumerate(['Blue', 'Green', 'Red']):
    axes[1, i + 1].hist(equalized_channels[i].ravel(), bins=256, color=color.lower(), alpha=0.7)
    axes[1, i + 1].set_title(f'Equalized {color} Channel Histogram', fontsize=FONT_SIZE)
    axes[1, i + 1].set_xlabel('Pixel Value', fontsize=FONT_SIZE)
    axes[1, i + 1].set_ylabel('Frequency', fontsize=FONT_SIZE)

# 调整子图布局
plt.tight_layout()
plt.show()

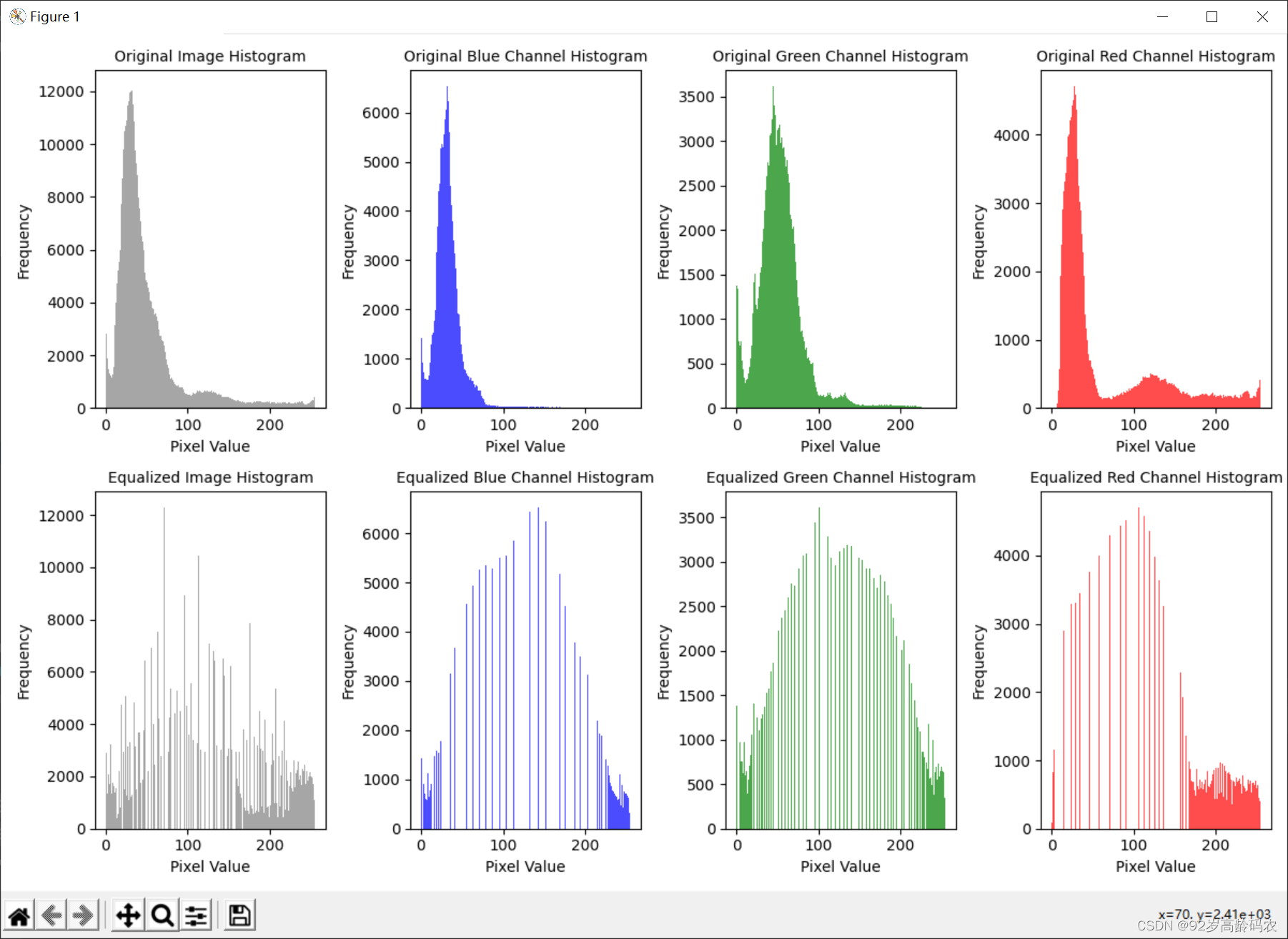
上述代码使用了cv2.equalizeHist()函数对图像进行直方图均衡化。cv2.equalizeHist(channel)，这个函数用于对单通道的图像进行直方图均衡化。对于彩色图像，需要将图像分离成各个通道，然后分别对每个通道进行均衡化，最后再合并通道。

具体而言，对于单通道的图像，该函数会计算图像的直方图，并对图像进行拉伸，使得图像的灰度值分布更加均匀。这有助于提高图像的对比度，使得细节更加清晰可见。

值得注意的是，直方图均衡化在某些情况下可能会增加噪音的影响，因此在实际应用中需要谨慎使用，并根据具体需求进行调整。

1.5 直方图自适应均衡化

直方图自适应均衡化是一种进一步改进的直方图均衡化方法，它考虑了图像局部区域的对比度差异。

1.5.1 直方图自适应均衡化原理

直方图自适应均衡化的核心思想是将图像分成多个小块，在每个小块内进行直方图均衡化。这样，可以根据每个小块的局部特性调整图像的对比度，从而在整体上实现更好的均衡效果。

1.5.2 直方图自适应均衡化公式

直方图自适应均衡化的数学表达式如下：

$$G(x,y)=T(x,y)-T_{\text{min}}\times (L-1)$$

其中：

• $G(x,y)$ 是均衡化后的像素值；
• $T(x,y)$ 是原始图像在位置$(x,y)$处的累积分布函数；
• $T_{\text{min}}$ 是原始图像中所有局部块的最小累积值；
• $L$ 是图像的灰度级数。

1.5.3 直方图自适应均衡化代码示例

下面是使用OpenCV进行直方图自适应均衡化的代码示例：

import cv2

# 读取图像
image = cv2.imread('tulips.jpg')

# 分离通道
b, g, r = cv2.split(image)

# 对每个通道进行CLAHE均衡化
clahe = cv2.createCLAHE(clipLimit=2.0, tileGridSize=(8, 8))
clahe_b = clahe.apply(b)
clahe_g = clahe.apply(g)
clahe_r = clahe.apply(r)

# 合并通道
clahe_image = cv2.merge([clahe_b, clahe_g, clahe_r])

# 显示原图和均衡化后的图像
cv2.imshow('Adaptive Equalized Image', cv2.hconcat([image, clahe_image]))
cv2.waitKey(0)
cv2.destroyAllWindows()

import matplotlib.pyplot as plt

# 创建Matplotlib子图
fig, axes = plt.subplots(2, 4, figsize=(12, 8))
FONT_SIZE = 10
# 显示原图的直方图
axes[0, 0].hist(image.ravel(), bins=256, color='gray', alpha=0.7)
axes[0, 0].set_title('Original Image Histogram', fontsize=FONT_SIZE)
axes[0, 0].set_xlabel('Pixel Value', fontsize=FONT_SIZE)
axes[0, 0].set_ylabel('Frequency', fontsize=FONT_SIZE)

# 显示原图的通道直方图
for i, color in enumerate(['Blue', 'Green', 'Red']):
    axes[0, i + 1].hist(image[:, :, i].ravel(), bins=256, color=color.lower(), alpha=0.7)
    axes[0, i + 1].set_title(f'Original {color} Channel Histogram', fontsize=FONT_SIZE)
    axes[0, i + 1].set_xlabel('Pixel Value', fontsize=FONT_SIZE)
    axes[0, i + 1].set_ylabel('Frequency', fontsize=FONT_SIZE)

# 显示CLAHE均衡化后的直方图
axes[1, 0].hist(clahe_image.ravel(), bins=256, color='gray', alpha=0.7)
axes[1, 0].set_title('CLAHE Equalized Image Histogram', fontsize=FONT_SIZE)
axes[1, 0].set_xlabel('Pixel Value', fontsize=FONT_SIZE)
axes[1, 0].set_ylabel('Frequency', fontsize=FONT_SIZE)

# 显示CLAHE均衡化后的通道直方图
for i, color in enumerate(['Blue', 'Green', 'Red']):
    axes[1, i + 1].hist(clahe_image[:, :, i].ravel(), bins=256, color=color.lower(), alpha=0.7)
    axes[1, i + 1].set_title(f'CLAHE Equalized {color} Channel Histogram', fontsize=FONT_SIZE)
    axes[1, i + 1].set_xlabel('Pixel Value', fontsize=FONT_SIZE)
    axes[1, i + 1].set_ylabel('Frequency', fontsize=FONT_SIZE)

# 调整子图布局
plt.tight_layout()
plt.show()

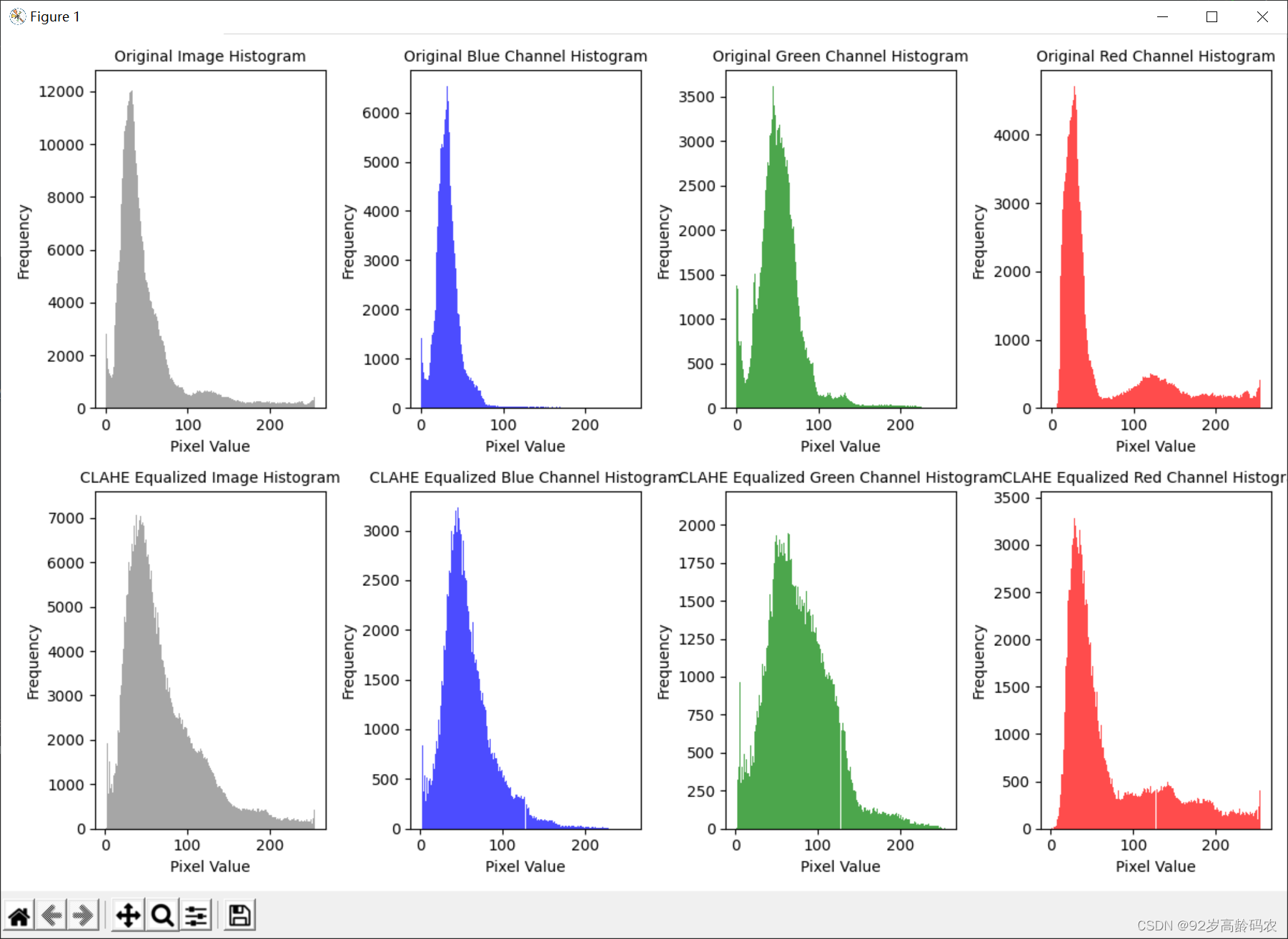
上述代码使用了cv2.createCLAHE()函数创建了一个对比度限制的自适应直方图均衡器（CLAHE），并对图像的红、绿、蓝三个通道分别进行均衡化。下面是对createCLAHE()函数的参数进行说明：

• clipLimit: 控制对比度的限制。这是一个关键参数，它规定了对比度增强的程度。如果设置得太高，可能会导致噪音的引入，而设置得太低可能无法产生显著的效果。根据实际情况进行调整。
• tileGridSize: 定义图像被分割的块的大小。CLAHE算法将图像分为多个小块，对每个小块进行直方图均衡化。tileGridSize参数决定了这些块的大小。一般而言，较小的块可以更好地应对图像中的局部对比度变化。

在这个例子中，createCLAHE()创建了一个CLAHE对象，并通过apply()方法将其应用于每个通道。最后，使用cv2.merge()函数将均衡化后的通道合并，得到均衡化后的图像。

1.5 直方图匹配

直方图匹配旨在调整图像的灰度分布，使其匹配预定义的目标分布。这对于使图像更符合特定的期望或标准分布非常有用。以下是直方图匹配的原理、公式和通过OpenCV实现的代码示例。

1.5.1 直方图匹配原理

直方图匹配的原理是通过变换图像的灰度级分布，使其接近目标分布。这种匹配可以通过以下步骤实现：

1. 计算原始图像和目标分布的累积分布函数（CDF）。
2. 将原始图像的每个像素值映射到目标CDF，从而调整灰度级分布。

1.5.2 直方图匹配公式

设原始图像的灰度级为 $r$，目标图像的灰度级为 $z$，原始图像的累积分布函数为 $P_r(r)$，目标图像的累积分布函数为 $P_z(z)$。则直方图匹配的映射关系为：

$$s=G(r)=P_z^{-1}(P_r(r))$$

其中，$s$ 是匹配后的像素值。

1.5.3 OpenCV代码示例

我们将tulips1.jpg的直方图分布映射到tulips2.jpg中。
tulips1.jpg

tulips2.jpg

以下是使用OpenCV进行直方图匹配的代码示例：

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取原始图像和目标图像
original_image = cv2.imread('tulips2.jpg', cv2.IMREAD_GRAYSCALE)
target_image = cv2.imread('tulips1.jpg', cv2.IMREAD_GRAYSCALE)
original_image = cv2.resize(original_image, target_image.shape[::-1])

# 计算原始图像和目标图像的直方图
original_hist = cv2.calcHist([original_image], [0], None, [256], [0, 256])
target_hist = cv2.calcHist([target_image], [0], None, [256], [0, 256])

# 将直方图归一化
original_hist /= original_image.size
target_hist /= target_image.size

# 计算原始图像和目标图像的累积分布函数
original_cdf = original_hist.cumsum()
target_cdf = target_hist.cumsum()

# 映射关系
mapping = np.interp(original_cdf, target_cdf, range(256)).astype(np.uint8)

# 应用映射关系进行直方图匹配
matched_image = mapping[original_image]

cv2.imshow("Matched Image", cv2.hconcat([original_image, target_image, matched_image]))
cv2.waitKey(0)
cv2.destroyAllWindows()

# 绘制直方图
plt.figure(figsize=(12, 4))

plt.subplot(131)
plt.title("Original Image Histogram")
plt.plot(original_hist)

plt.subplot(132)
plt.title("Target Image Histogram")
plt.plot(target_hist)

plt.subplot(133)
plt.title("Matched Image Histogram")
matched_hist = cv2.calcHist([matched_image], [0], None, [256], [0, 256])
matched_hist /= matched_image.size
plt.plot(matched_hist)

plt.show()

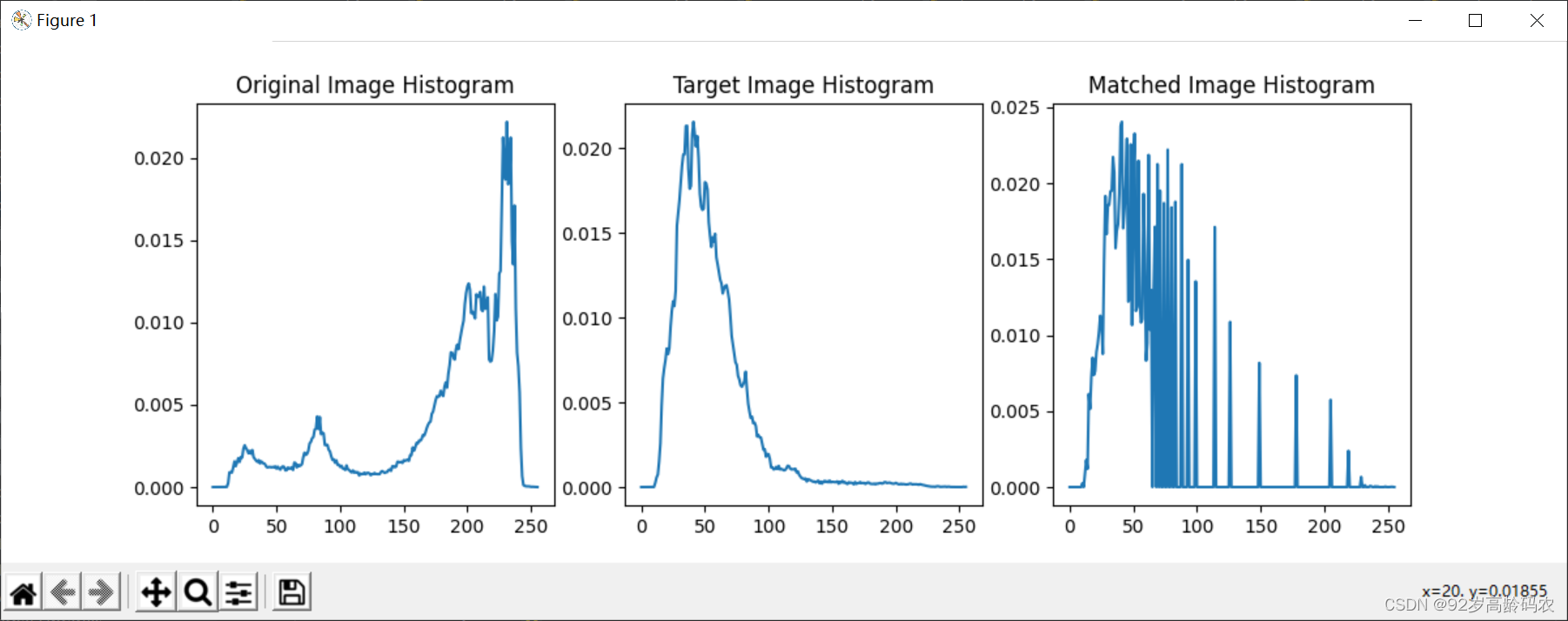
在这个示例中，我们首先读取原始图像和目标图像，然后计算它们的直方图，并将直方图归一化。接下来，计算原始图像和目标图像的累积分布函数，并通过插值计算映射关系。最后，应用映射关系对原始图像进行直方图匹配，生成匹配后的图像。

二、掩膜技术

2.1 掩膜的基本原理

2.1.1 定义

掩膜是一种用于选择性地处理图像特定区域的工具，它通过在图像上应用一个二值化的图层，将需要处理的区域标记为白色（255），而将不需要处理的区域标记为黑色（0）。

2.1.2 作用

• 选择性处理： 掩膜允许在图像中选择性地应用滤波、增强或其他图像处理操作，以便集中处理感兴趣的区域。
• 区域分割： 掩膜可用于分割图像，将图像分为不同的区域，以便独立处理每个区域。

2.1.3 原理

在OpenCV中，掩膜操作通过将掩膜与原始图像进行逐元素的逻辑运算来实现。这意味着对于掩膜中的每个像素，如果其值为白色（255），则相应位置的原始图像像素将被保留，否则将被抑制。

2.1.4 公式

$$\text{Output}(x,y)=\text{Image}(x,y)\text{if}\text{Mask}(x,y)\ne 0\text{else}0$$

2.2 掩膜的代码示例

以下是使用OpenCV进行掩膜操作的代码示例：

import cv2
import numpy as np

# 读取图像
image = cv2.imread('tulips.jpg')
# 将图像转换为灰度图
gray_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

# 创建一个黑色的图像作为掩膜
mask = np.zeros_like(gray_image, dtype=np.uint8)
# 获取图像中心坐标
center = (400, 200)
# 生成圆形掩膜
radius = 70
color = 255  # 白色
cv2.circle(mask, center, radius, color, thickness=-1, lineType=cv2.LINE_AA)
# 应用掩膜
masked_gray_image = cv2.bitwise_and(gray_image, mask)

# 计算直方图
hist_gray = cv2.calcHist([gray_image], [0], None, [256], [0, 256])
hist_mask = cv2.calcHist([gray_image], [0], mask, [256], [0, 256])

# 显示直方图
hist_gray_image = np.zeros((256, 256), dtype=np.uint8)
cv2.normalize(hist_gray, hist_gray, 0, 255, cv2.NORM_MINMAX)
hist_gray = np.int32(np.around(hist_gray))
for i in range(256):
    cv2.line(hist_gray_image, (i, 255), (i, 255 - hist_gray[i]), 255, lineType=cv2.LINE_AA)
hist_gray_image = cv2.resize(hist_gray_image, gray_image.shape[::-1])

hist_mask_image = np.zeros((256, 256), dtype=np.uint8)
cv2.normalize(hist_mask, hist_mask, 0, 255, cv2.NORM_MINMAX)
hist_mask = np.int32(np.around(hist_mask))
for i in range(256):
    cv2.line(hist_mask_image, (i, 255), (i, 255 - hist_mask[i]), 255, lineType=cv2.LINE_AA)
hist_mask_image = cv2.resize(hist_mask_image, gray_image.shape[::-1])

# 显示原图、灰度图和掩膜操作后的图像
cv2.imshow('Masked Gray Image', cv2.vconcat([
    cv2.hconcat([gray_image, masked_gray_image]),
    cv2.hconcat([hist_gray_image, hist_mask_image])
    ]))
cv2.waitKey(0)
cv2.destroyAllWindows()

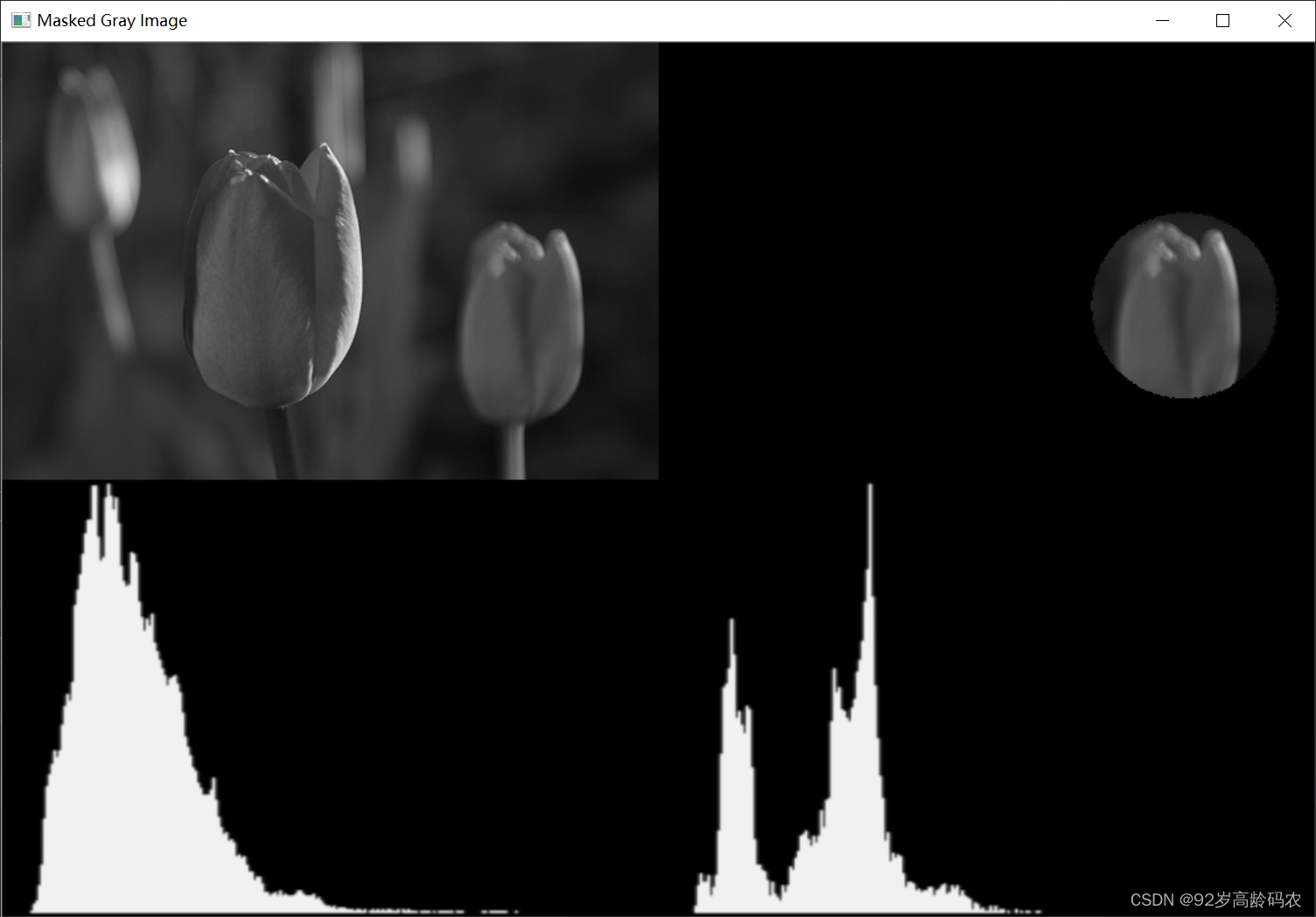
下面重点解释一下hist_mask = cv2.calcHist([gray_image], [0], mask, [256], [0, 256])

• cv2.calcHist: 这是计算直方图的函数。
• [gray_image]: 这是一个包含图像的列表。在这里，我们计算灰度图像的直方图，因此列表中只包含了灰度图像 gray_image。
• [0]: 这是指定通道的参数。对于灰度图像，只有一个通道，因此我们使用 [0] 表示第一个通道。
• mask: 这是掩膜，用于指定计算直方图的区域。在这里，直方图将仅计算掩膜中对应像素位置为白色的区域。
• [256]: 这是指定直方图的 bin 的数量，即直方图中有多少个条形。
• [0, 256]: 这是指定像素值的范围，即直方图的 x 轴范围。在这里，表示从 0 到 255。

三、模板匹配

3.1 模板匹配的基本原理

3.1.1 原理

模板匹配是一种在图像中寻找特定模式或对象的技术。其基本原理是通过在输入图像中滑动一个模板（也称为内核或窗口），在每个位置计算模板与图像局部区域的相似度，找到相似度最高的位置，从而定位目标。

3.1.2 公式

在模板匹配中，OpenCV提供了不同的匹配方法，其中包括了一些常见的相关性系数的计算方法。
以下是这些匹配方法的名称和对应的公式：

1. TM_CCOEFF (相关性系数)

   • 方法名称：cv2.TM_CCOEFF
   • 公式：$$R(u,v)=\sum _{x,y}[T(x,y)\cdot I(x+u,y+v)]$$

2. TM_CCOEFF_NORMED (归一化相关性系数)

   • 方法名称：cv2.TM_CCOEFF_NORMED
   • 公式：$$R(u,v)=\frac{{\sum }_{x,y}[T(x,y)\cdot I(x+u,y+v)]}{\sqrt{{\sum }_{x,y}T(x,y{)}^2\cdot {\sum }_{x,y}I(x+u,y+v{)}^2}}$$

3. TM_CCORR (相关性匹配)

   • 方法名称：cv2.TM_CCORR
   • 公式：$$R(u,v)=\sum _{x,y}[T(x,y)\cdot I(x+u,y+v)]$$

4. TM_CCORR_NORMED (归一化相关性匹配)

   • 方法名称：cv2.TM_CCORR_NORMED
   • 公式：$$R(u,v)=\frac{{\sum }_{x,y}[T(x,y)\cdot I(x+u,y+v)]}{\sqrt{{\sum }_{x,y}T(x,y{)}^2\cdot {\sum }_{x,y}I(x+u,y+v{)}^2}}$$

5. TM_SQDIFF (平方差匹配)

   • 方法名称：cv2.TM_SQDIFF
   • 公式：$$R(u,v)=\sum _{x,y}[T(x,y)-I(x+u,y+v){]}^2$$

6. TM_SQDIFF_NORMED (归一化平方差匹配)

   • 方法名称：cv2.TM_SQDIFF_NORMED
   • 公式：$$R(u,v)=\frac{{\sum }_{x,y}[T(x,y)-I(x+u,y+v){]}^2}{\sqrt{{\sum }_{x,y}T(x,y{)}^2\cdot {\sum }_{x,y}I(x+u,y+v{)}^2}}$$

其中，$T(x,y)$ 是模板中的像素值，$I(x+u,y+v)$ 是图像中偏移为 $(u,v)$ 的局部区域的像素值。这些公式描述了每个匹配方法中的相似性度量，它们在模板匹配中用于确定模板与图像局部区域的匹配程度。

3.2 OpenCV中的模板匹配函数

3.2.1 函数

OpenCV提供了 cv2.matchTemplate() 函数来执行模板匹配。该函数在输入图像上滑动模板，并在每个位置计算模板与图像局部区域的相关性。

函数方法：
cv2.matchTemplate(image, templ, method[, result[, mask]])

函数参数：

• image: 进行搜索的图像，必须为8位或32位浮点型。
• templ: 要搜索的模板，其大小不能超过源图像，且数据类型需相同。
• method: 指定比较方法，见3.1.2 公式。
• result (可选): 比较结果的映射。必须为单通道32位浮点型。如果图像大小为 $\text{W}\times \text{H}$，模板大小为 $w\times h$，那么结果大小为 $(\text{W}-w+1)\times (\text{H}-h+1)$。
• mask (可选): 搜索模板的掩膜，必须与模板具有相同的数据类型和大小。默认值为 None。目前仅支持 #TM_SQDIFF 和 #TM_CCORR_NORMED 方法。

函数说明：

该函数通过在图像上滑动模板，在每个位置计算模板与图像局部区域的相似度，并将比较结果存储在 result 中。比较方法由 method 参数指定。函数返回比较结果，该结果可以通过 cv2.minMaxLoc() 函数找到最佳匹配位置。

在彩色图像中，对于模板中的每个通道和每个通道中的每个和，使用分别计算的均值进行求和。因此，该函数可以处理彩色模板和彩色图像，但返回的是单通道图像，更容易进行分析。

返回值：

返回一个单通道图像，大小为 $(\text{W}-w+1)\times (\text{H}-h+1)$，表示模板在图像中的比较结果。

3.2.2 代码示例

以下是一个简单的OpenCV模板匹配的代码示例：

import cv2
import numpy as np

# 生成黑色画布
height, width = 300, 400
canvas = np.zeros((height, width, 3), dtype=np.uint8)

# 随机生成一些彩色圆形
num_circles = 20
radius = 20
for _ in range(num_circles):
    center = (np.random.randint(0, width), np.random.randint(0, height))
    color = (np.random.randint(0, 256), np.random.randint(0, 256), np.random.randint(0, 256))
    cv2.circle(canvas, center, radius, color, -1)

# 生成白色模板
template = np.zeros((radius * 2, radius * 2, 3), dtype=np.uint8)
cv2.circle(template, (radius, radius), radius, (255, 255, 255), -1)

# 转为灰度图像进行匹配
gray_canvas = cv2.cvtColor(canvas, cv2.COLOR_BGR2GRAY)
gray_template = cv2.cvtColor(template, cv2.COLOR_BGR2GRAY)

# 使用cv2.matchTemplate进行匹配
result = cv2.matchTemplate(gray_canvas, gray_template, cv2.TM_CCOEFF_NORMED)
threshold = 0.7  # 设定匹配阈值

# 获取匹配结果的位置
locations = np.where(result >= threshold)
locations = list(zip(*locations[::-1]))


# 非最大抑制 (NMS) 防止相邻重复匹配
def non_max_suppression(rectangles):
    if not rectangles:
        return []

    rectangles = sorted(rectangles, key=lambda x: x[2], reverse=True)
    picked = [rectangles[0]]

    for current in rectangles:
        _, _, current_right, current_bottom = current
        to_pick = True

        for previous in picked:
            _, _, previous_right, previous_bottom = previous

            if (current_right > previous[0] and
                current[0] < previous_right and
                current_bottom > previous[1] and
                current[1] < previous_bottom):
                to_pick = False
                break

        if to_pick:
            picked.append(current)

    return picked


# 在原图上框出匹配的圆形
rectangles = []
for loc in locations:
    top_left = loc
    bottom_right = (top_left[0] + template.shape[1], top_left[1] + template.shape[0])
    rectangles.append((*top_left, *bottom_right))

picked_rectangles = non_max_suppression(rectangles)
for rect in picked_rectangles:
    top_left = rect[:2]
    bottom_right = rect[2:]
    cv2.rectangle(canvas, top_left, bottom_right, (0, 255, 0), 2)

# 显示结果
cv2.imshow('Canvas', canvas)
cv2.imshow('Template', template)
cv2.waitKey(0)
cv2.destroyAllWindows()

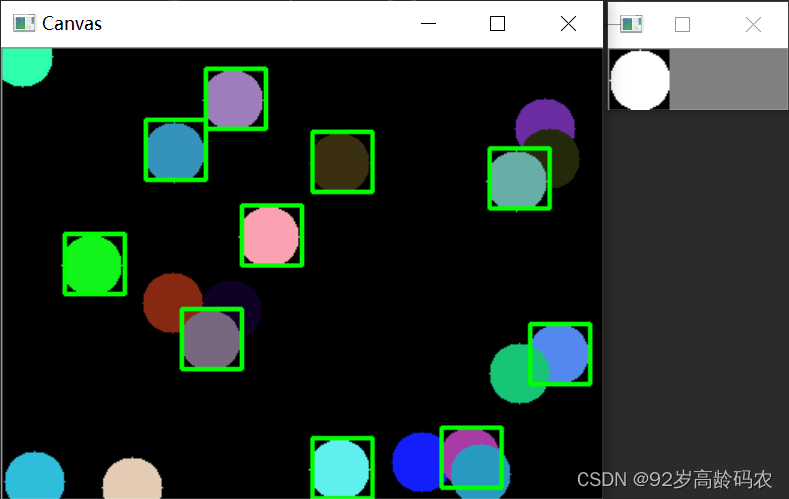
这段代码演示了在一个黑色画布上生成随机彩色圆形，并在生成的画布上使用模板匹配的方法找到与白色模板匹配的圆形。
主要的思路为：

1. 生成黑色画布： 通过np.zeros函数生成一个黑色画布，height和width分别表示画布的高度和宽度。

2. 生成随机彩色圆形： 通过循环生成一定数量的随机位置和颜色的圆形，使用cv2.circle函数在画布上绘制这些圆形。

3. 生成白色模板： 创建一个白色模板，该模板是一个白色圆形，用于后续模板匹配。

4. 转为灰度图像进行匹配： 将彩色画布和白色模板分别转换为灰度图像，为了进行模板匹配，使用cv2.cvtColor函数。

5. 使用cv2.matchTemplate进行匹配： 利用cv2.matchTemplate函数进行模板匹配，使用cv2.TM_CCOEFF_NORMED作为匹配算法。

6. 设定匹配阈值： 设定一个匹配阈值，筛选出匹配程度高于阈值的位置。

7. 获取匹配结果的位置： 通过np.where函数找到匹配程度高于阈值的位置。

8. 非最大抑制 (NMS) 防止相邻重复匹配： 实现非最大抑制函数，用于防止相邻区域的重复匹配。非最大抑制的思路是： 首先按照相似度降序排列所有矩形框，然后从高相似度的矩形框开始，将与之相交的其他矩形框从候选集中移除。最终，得到的 picked_rectangles 是经过非最大抑制后的矩形框列表。

9. 在原图上框出匹配的圆形： 遍历匹配位置，用绿色矩形框出匹配的圆形，通过非最大抑制确保不会重复框出相似的区域。

10. 显示结果： 利用cv2.imshow函数显示画布和模板的匹配结果。

3.3 模板匹配在实际场景中的应用

3.3.1 应用举例

1.目标检测： 模板匹配可用于在图像中检测特定对象或目标，例如在监控摄像头中识别人脸。

2.物体跟踪： 模板匹配可以用于跟踪视频序列中的运动物体，通过在每一帧中寻找匹配模板的位置。

3.图像分析： 在图像分析中，模板匹配可用于寻找图像中特定模式的位置，从而进行进一步的分析和处理。

3.2.2 代码示例

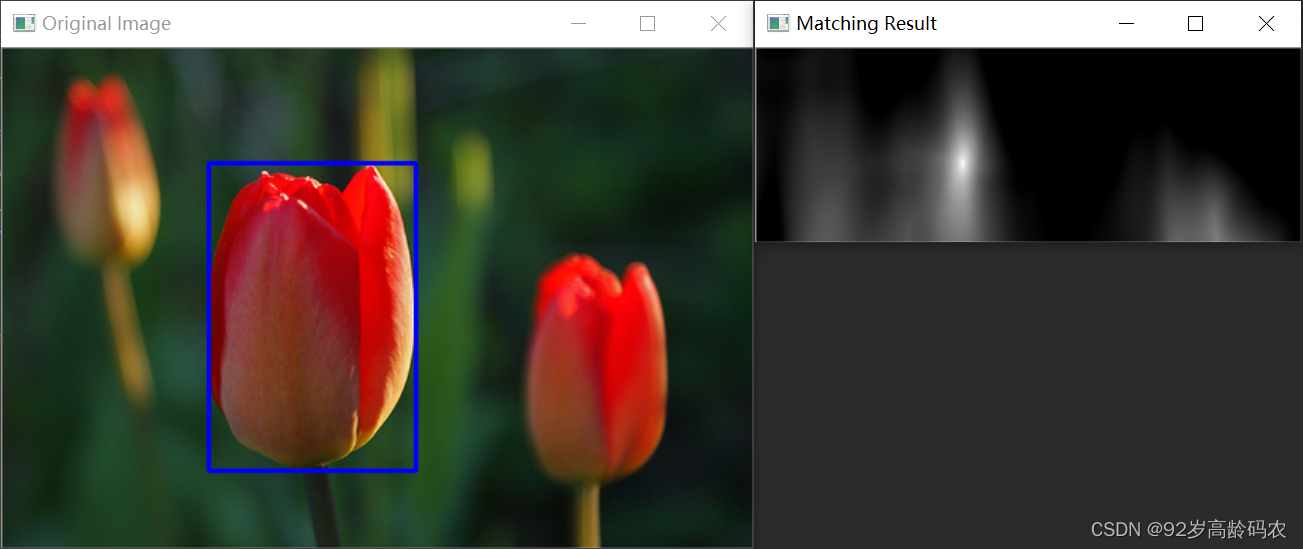
首先，我们从测试图中抠出想要的图片作为tulips_template.jpg

以下是一个简单的OpenCV模板匹配的代码示例：

import cv2

# 读取图像和模板
image = cv2.imread('tulips.jpg')
template = cv2.imread('tulips_template.jpg')

# 使用模板匹配函数
result = cv2.matchTemplate(image, template, cv2.TM_CCOEFF_NORMED)

# 获取匹配结果的位置
min_val, max_val, min_loc, max_loc = cv2.minMaxLoc(result)

# 在原始图像上绘制矩形框标记匹配位置
h, w = template.shape[:2]
top_left = max_loc
bottom_right = (top_left[0] + w, top_left[1] + h)
cv2.rectangle(image, top_left, bottom_right, 255, 2)

# 显示原始图像和标记匹配位置的图像
cv2.imshow('Original Image', image)
cv2.imshow('Matching Result', result)
cv2.waitKey(0)
cv2.destroyAllWindows()

四、霍夫变换

4.1 霍夫变换的概念

4.1.1 霍夫变换原理

霍夫变换是一种用于检测图像中特定几何形状的技术。最常见的应用是检测直线和圆。在霍夫变换中，图像中的每个点都被映射到参数空间（霍夫空间）中，形成一组曲线。这些曲线在参数空间中的交点表示图像中存在特定形状。

直线和圆霍夫变换是其中最常用的形式，它们在计算机视觉和图像处理中有着广泛的应用。

直线霍夫变换

对于直线霍夫变换，每个点在霍夫空间中映射为一组曲线，这些曲线表示图像中可能存在的直线。在直线的极坐标表示中，一条直线可以由两个参数表示：极径 $\rho$ 和极角 $\theta$。每个点映射为一组曲线，其中每条曲线对应于可能通过该点的一条直线。

圆霍夫变换

对于圆霍夫变换，每个图像中的点在霍夫空间中映射为一组曲线，表示可能存在的圆。在圆的参数表示中，一个圆可以由三个参数表示：圆心坐标 $(a,b)$ 和半径 $r$。每个点映射为一组曲线，其中每条曲线对应于可能通过该点的一个圆。

4.1.2 霍夫变换的步骤

1. 参数空间初始化： 根据待检测形状的参数个数，初始化霍夫空间。对于直线，通常使用极坐标表示，因此霍夫空间是一个二维数组，表示 $(\rho ,\theta )$。

2. 映射： 将图像中的每个点映射到霍夫空间，形成一组曲线。

3. 累加： 在霍夫空间中累加曲线交点的值，找到共享最大累积点的位置。

4. 阈值处理： 根据设定的阈值，确定霍夫空间中的峰值，这些峰值对应于图像中存在的形状。

5. 反映射： 将霍夫空间中的峰值反映射回图像空间，得到检测到的形状的参数。

4.1.3 霍夫变换的公式

直线霍夫变换：

直线的极坐标方程为：

$$\rho =x\cdot \cos (\theta )+y\cdot \sin (\theta )$$

其中，$(\rho ,\theta )$ 是直线在霍夫空间中的表示，$(x,y)$ 是图像中的点坐标。

圆霍夫变换：

圆的参数方程为：

$$(x-a{)}^2+(y-b{)}^2=r^2$$

其中，$(a,b)$ 是圆心坐标，$r$ 是半径。

4.2 直线霍夫变换

4.2.1 霍夫变换的基本原理

直线霍夫变换基于直线的极坐标方程。在霍夫变换中，每个图像上的点都映射到霍夫空间中的一组曲线，这些曲线交于一点，表示原始图像中存在一条直线。通过在霍夫空间中找到交点最多的曲线，可以确定原始图像中的直线。

4.2.2 OpenCV中的直线霍夫变换

OpenCV提供了cv2.HoughLines()和cv2.HoughLinesP()函数来执行直线霍夫变换。该函数返回一组直线的参数，通常使用极坐标表示（rho, theta）。

import cv2
import numpy as np

# 生成一张黑色画布
height, width = 300, 400
image = np.zeros((height, width, 3), dtype=np.uint8)

# 随机生成一些点、线、圆和矩形
num_points = 30
points = np.random.randint(0, height, size=(num_points, 2))
num_lines = 2
lines = np.random.randint(0, height, size=(num_lines, 2, 2))
num_circles = 1
circles = np.random.randint(0, height, size=(num_circles, 3))
num_rectangles = 1
rectangles = np.random.randint(0, height, size=(num_rectangles, 2, 2))

# 在画布上绘制这些形状
for point in points:
    cv2.circle(image, tuple(point), 3, (0, 0, 255), -1)

for line in lines:
    cv2.line(image, tuple(line[0]), tuple(line[1]), (255, 0, 0), 2)

for circle in circles:
    cv2.circle(image, tuple(circle[:2]), circle[2], (255, 0, 255), 2)

for rectangle in rectangles:
    cv2.rectangle(image, tuple(rectangle[0]), tuple(rectangle[1]), (0, 255, 255), 2)

# 将图像转为灰度
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

# 使用边缘检测
edges = cv2.Canny(gray, 50, 150)

# 使用霍夫线变换检测直线
lines_detected = cv2.HoughLines(edges, 1, np.pi / 180, threshold=50)

# 使用概率霍夫线变换检测直线
lines_p_detected = cv2.HoughLinesP(edges, 1, np.pi / 180, threshold=50, minLineLength=30, maxLineGap=10)

image_p = image.copy()

# 绘制检测到的直线（HoughLines）
if lines_detected is not None:
    for line in lines_detected:
        rho, theta = line[0]
        a = np.cos(theta)
        b = np.sin(theta)
        x0 = a * rho
        y0 = b * rho
        x1 = int(x0 + 1000 * (-b))
        y1 = int(y0 + 1000 * (a))
        x2 = int(x0 - 1000 * (-b))
        y2 = int(y0 - 1000 * (a))
        cv2.line(image, (x1, y1), (x2, y2), (0, 255, 0), 2)

# 绘制检测到的直线（HoughLinesP）
if lines_p_detected is not None:
    for line in lines_p_detected:
        x1, y1, x2, y2 = line[0]
        cv2.line(image_p, (x1, y1), (x2, y2), (0, 255, 0), 2)

# 显示结果
edges_bgr = cv2.merge([edges, edges, edges])
cv2.imshow('Hough Lines Detection', cv2.hconcat([image, image_p, edges_bgr]))
cv2.waitKey(0)
cv2.destroyAllWindows()

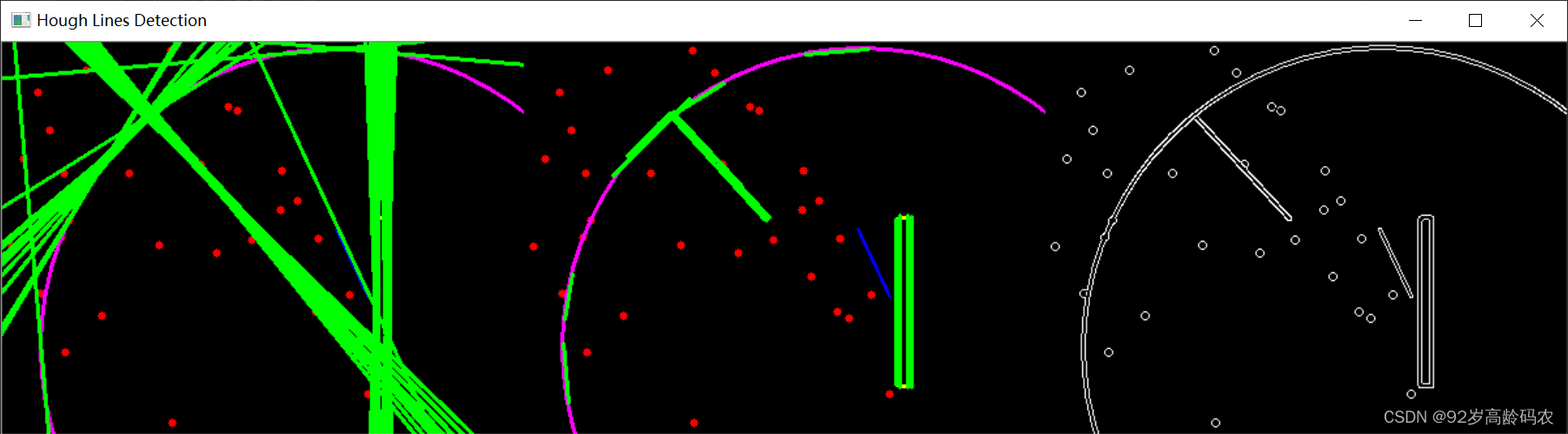
使用霍夫线变换检测直线
霍夫线变换是一种经典的图像处理技术，用于检测图像中的直线。在OpenCV中，cv2.HoughLines函数用于执行标准霍夫线变换，它接受以下参数：

• edges: 边缘检测后的图像，通常通过Canny等边缘检测算法获得。
• rho: 霍夫空间中的距离分辨率，以像素为单位。一般设为1。
• theta: 霍夫空间中的角度分辨率，以弧度为单位。一般设为np.pi / 180，表示每个角度取一个弧度。
• threshold: 阈值，用于确定检测到的直线的强度。高于此阈值的直线将被保留。

通过调用cv2.HoughLines，我们可以获得检测到的直线的参数，通常表示为(rho, theta)。

使用概率霍夫线变换检测直线

概率霍夫线变换是对标准霍夫线变换的改进，通过引入概率采样的方式，减少了计算量。在OpenCV中，cv2.HoughLinesP函数执行概率霍夫线变换，它接受的参数与cv2.HoughLines类似，并额外包括：

• minLineLength: 最小线段长度，小于此长度的线段将被忽略。
• maxLineGap: 最大线段间隙，超过此间隙的线段将被认为是两条不同的线段。

通过调用cv2.HoughLinesP，我们可以获得检测到的线段的端点坐标，表示为(x1, y1, x2, y2)。

这两种方法返回的检测结果可以用于在图像上绘制检测到的直线或线段，为图像处理和计算机视觉任务提供了强大的工具。

4.3 圆霍夫变换

4.3.1 圆霍夫变换的原理

圆霍夫变换通过对图像进行霍夫梯度法的处理来检测图像中的圆形结构。这种方法基于图像中的边缘信息，使用梯度的方向和大小来确定可能是圆的位置。

以下是圆霍夫变换的基本原理：

1. 梯度计算： 在图像中计算梯度，通常使用Sobel算子等边缘检测算子。梯度的方向和大小信息对于检测边缘很关键。

2. 霍夫梯度法： 对每个像素点，根据其梯度方向，在累加器中沿着可能的圆的半径和圆心位置进行投票。这样，对于每个可能的圆，都有一个相应的累加器。

3. 累加器峰值检测： 在累加器中找到峰值，这表示圆心和半径的可能位置。峰值的强度表示有多少梯度方向的边缘共享相同的圆心和半径。

4. 圆心和半径的筛选： 根据设定的阈值，筛选出累加器中强度高于阈值的峰值，这些峰值对应于图像中的圆。

4.3.2 OpenCV中的圆霍夫变换

OpenCV提供了cv2.HoughCircles()函数来执行圆霍夫变换。该函数返回检测到的圆的参数。

import cv2
import numpy as np

# 生成一张黑色画布
height, width = 300, 400
image = np.zeros((height, width, 3), dtype=np.uint8)

# 随机生成一些点、线、圆和矩形
num_points = 30
points = np.random.randint(0, height, size=(num_points, 2))
num_lines = 2
lines = np.random.randint(0, height, size=(num_lines, 2, 2))
num_circles = 5
circles = np.random.randint(0, height, size=(num_circles, 3))
num_rectangles = 1
rectangles = np.random.randint(0, height, size=(num_rectangles, 2, 2))

# 在画布上绘制这些形状
for point in points:
    cv2.circle(image, tuple(point), 2, (0, 0, 255), -1)

for line in lines:
    cv2.line(image, tuple(line[0]), tuple(line[1]), (255, 0, 0), 3)

for circle in circles:
    cv2.circle(image, tuple(circle[:2]), circle[2], (255, 0, 255), 3)

for rectangle in rectangles:
    cv2.rectangle(image, tuple(rectangle[0]), tuple(rectangle[1]), (0, 255, 255), 3)

# 将图像转为灰度
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

# 定义矩形结构元素
rectangle_kernel = cv2.getStructuringElement(cv2.MORPH_RECT, (3, 3))
# 开运算操作
gray = cv2.morphologyEx(gray, cv2.MORPH_OPEN, rectangle_kernel)
# 中值滤波
gray = cv2.medianBlur(gray, 5)

# 使用霍夫圆变换检测圆
circles_detected = cv2.HoughCircles(
    gray, cv2.HOUGH_GRADIENT, dp=1, minDist=100, param1=200, param2=30, minRadius=3, maxRadius=300
)

# 绘制检测到的圆
if circles_detected is not None:
    circles_detected = np.uint16(np.around(circles_detected))
    for circle in circles_detected[0, :]:
        center = (circle[0], circle[1])
        radius = circle[2]
        cv2.circle(image, center, radius, (0, 255, 0), 2)

# 显示结果
# 显示结果
gray_bgr = cv2.merge([gray, gray, gray])
cv2.imshow('Hough Circles Detection',  cv2.hconcat([image, gray_bgr]))
cv2.waitKey(0)
cv2.destroyAllWindows()

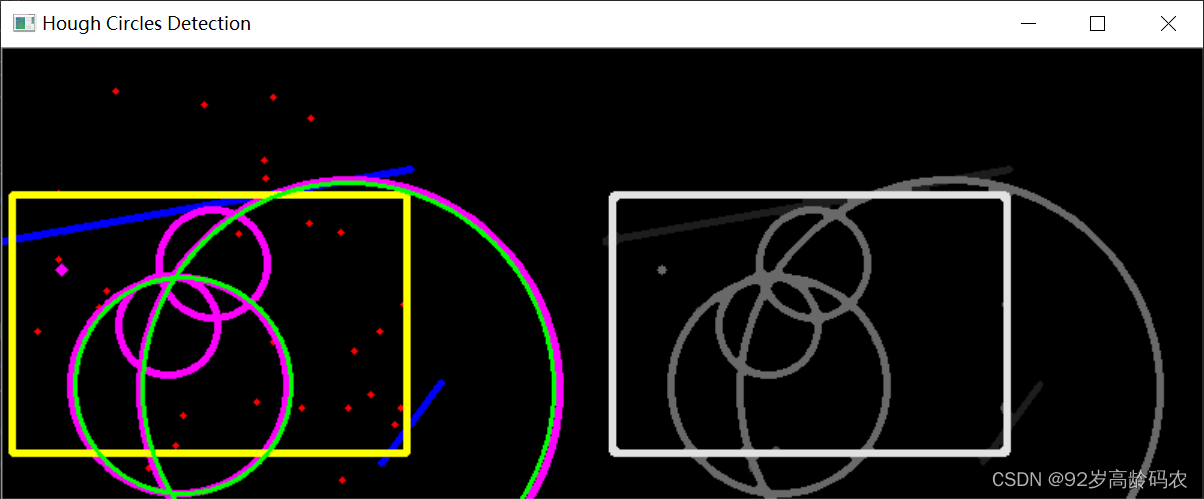
在上面的代码中，检测到的不是圆的部分可能是由于参数的选择不合适导致的。以下是一些参数的解释和调整建议：

• dp: 累加器分辨率与图像分辨率的倒数。如果设置得太小，可能导致检测到重复的圆。建议适度增加这个值，例如设置为2。
• minDist: 检测到的圆之间的最小距离。如果设置得太小，可能导致检测到重复的圆。建议适度增加这个值，例如设置为50。
• param1: Canny边缘检测的高阈值。可以适度调整这个值，使得边缘检测结果更符合实际情况。
• param2: 累加器阈值，高于此阈值的圆将被返回。可以适度调整这个值，以控制检测到的圆的数量。
• minRadius: 圆的最小半径。
• maxRadius: 圆的最大半径。

通过调整这些参数，可以更好地适应不同的图像和场景，提高圆检测的准确性。

总结

本文简要探讨了图像处理中的关键技术：直方图操作、掩膜技术、模板匹配以及霍夫变换。

首先，详细介绍了直方图的概念、生成方法和归一化技术，通过OpenCV的实际代码演示了直方图处理的过程。

接着，深入研究了掩膜技术，解释了其基本原理、作用和应用，通过OpenCV展示了掩膜的操作过程。

在模板匹配部分，探讨了模板匹配的基本原理、OpenCV中的相关函数以及实际应用场景，通过代码示例展示了模板匹配的过程。

最后，深入剖析了霍夫变换的概念、直线霍夫变换和圆霍夫变换的原理，通过OpenCV代码演示了霍夫变换在检测几何形状中的应用。

本文通过理论解析和实际代码示例，系统性地介绍了图像处理领域的关键技术，提供了深入学习和实践的基础。这些技术不仅在图像处理领域有广泛应用，同时也为计算机视觉和图像分析等领域提供了基础工具。