当前位置：首页 > article >正文

EI论文程序：Adaboost-BP神经网络的回归预测算法，可作为深度学习对比预测模型，丰富实验内容，自带数据集，直接运行！

article 2024/9/17 3:06:47

适用平台：Matlab 2021及以上

本程序参考中文EI期刊《基于Adaboost的BP神经网络改进算法在短期风速预测中的应用》，程序注释清晰，干货满满，下面对文章和程序做简要介绍。

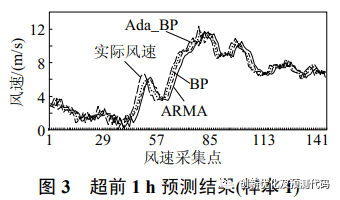
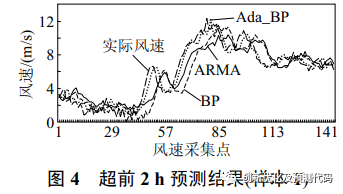
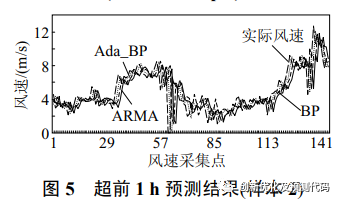
为了提高短期风速预测的准确性，论文提出了使用Adaboost算法来增强BP神经网络算法的方法。Adaboost算法是一种强大的学习算法，它通过组合弱学习器来提高整体预测能力。论文通过示例分析展示了Adaboost-BP神经网络方法在1到2小时风速预测中相比其他算法：ARMA、BP等具有更高的准确性，并强调了该方法在工程应用上的价值。

Adaboost-BP是一种集成学习方法，结合了Adaboost和BP（Back Propagation）神经网络的原理。Adaboost是一种Boosting算法，它通过集成多个弱预测器（通常是简单的学习器），以提高整体模型的性能。BP神经网络是一种常见的人工神经网络，用于模拟和学习复杂的非线性关系。

以下是Adaboost-BP的原理：

Adaboost原理：

Adaboost的核心思想是通过迭代训练一系列弱预测器，并赋予每个预测器一个权重，以调整其在最终模型中的贡献。

在每次迭代中，Adaboost调整训练样本的权重，使之前分类错误的样本在下一轮得到更多关注。

最终，所有弱预测器的预测结果通过加权求和得到最终模型的输出。

BP神经网络原理：

BP神经网络是一种前馈神经网络，它由输入层、隐藏层（可以有多层）、输出层组成。

神经网络通过前向传播计算输出，然后通过反向传播调整权重，以最小化预测误差。

反向传播使用梯度下降法更新权重，通过计算损失函数对权重的偏导数来确定梯度方向。

Adaboost-BP的结合：

在Adaboost-BP中，每个迭代中使用一个BP神经网络作为弱预测器。

初始时，所有样本的权重相等。

在每轮训练中，使用当前样本权重训练BP神经网络，并根据网络的性能（预测准确度）调整权重。

训练完一个BP神经网络后，计算其在整体模型中的权重，然后更新样本权重，以便下一轮训练中更关注之前预测精度低的样本。

重复这个过程直到达到预定的迭代次数或模型性能满足要求。

最终模型的预测：

最终模型是所有弱预测器的加权组合，每个弱预测器的权重由其在训练过程中的性能确定。

预测时，通过对每个弱预测器的预测结果进行加权求和，得到最终的模型输出。

Adaboost-BP的优点在于它结合了Adaboost和神经网络的优势，能够更好地处理复杂的非线性关系，提高模型的泛化能力。然而，也需要注意到该方法在训练过程中可能会更加复杂和耗时。

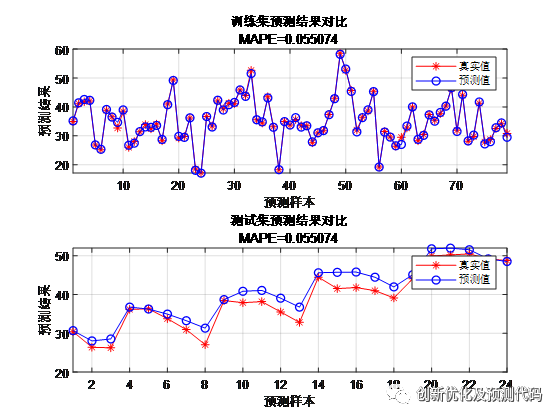
程序输出结果：

Adaboost-BP部分代码

%% Adaboost-BP预测
K=10;
for i=1:K
    
    %弱预测器训练
    net=newff(inputn,outputn,5);
    net.trainParam.epochs=20;
    net.trainParam.lr=0.1;
    net=train(net,inputn,outputn);
    
    %弱预测器预测
    an1=sim(net,inputn);
    T_sim1=mapminmax('reverse',an1,outputps);
    
    %预测误差
    erroryc(i,:)=T_train-T_sim1;

    %测试数据预测
    inputn1=mapminmax('apply',P_test ,inputps);
    an2=sim(net,inputn1);
    test_simu(i,:)=mapminmax('reverse',an2,outputps);% 各个弱预测器预测结果
    
    %调整D值
    Error(i)=0;
    for j=1:nn
        if abs(erroryc(i,j))>0.2  %较大误差
            Error(i)=Error(i)+D(i,j);
            D(i+1,j)=D(i,j)*1.1;
        else
            D(i+1,j)=D(i,j);
        end
    end
    
    %计算弱预测器权重
    at(i)=0.5/exp(abs(Error(i)));
    
    %D值归一化
    D(i+1,:)=D(i+1,:)/sum(D(i+1,:));
end

%% 强预测器预测
at=at/sum(at);

%% 强学习器学习预测结果
T_sim2=at*test_simu;

%%  计算各项误差参数 
error = T_sim2-T_test;               % 测试值和真实值的误差  
[~,len]=size(T_test);                % len获取测试样本个数，数值等于testNum，用于求各指标平均值
SSE1=sum(error.^2);                  % 误差平方和
MAE1=sum(abs(error))/len;            % 平均绝对误差
MSE1=error*error'/len;               % 均方误差
RMSE1=MSE1^(1/2);                    % 均方根误差
MAPE1=mean(abs(error./T_test));      % 平均百分比误差
r=corrcoef(T_test,T_sim2);           % corrcoef计算相关系数矩阵，包括自相关和互相关系数
R1=r(1,2);    

%%  绘图
figure
subplot(2, 1, 1)
plot(1: M, T_train, 'r-*', 1: M, T_sim1, 'b-o', 'LineWidth', 1)
legend('真实值', '预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'训练集预测结果对比'; ['MAPE=' num2str(MAPE1)]};
title(string)
xlim([1, M])
grid

subplot(2, 1, 2)
plot(1: N, T_test, 'r-*', 1: N, T_sim2, 'b-o', 'LineWidth', 1)
legend('真实值', '预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'测试集预测结果对比'; ['MAPE=' num2str(MAPE1)]};
title(string)
xlim([1, N])
grid

部分图片来源于网络，侵权联系删除！

欢迎感兴趣的小伙伴关注下方公众号获得完整版代码，小编会继续推送更有质量的学习资料、文章和程序代码！