nn.KLDivLoss,nn.CrossEntropyLoss,nn.MSELoss,Focal_Loss

1. KL loss：https://blog.csdn.net/qq_50001789/article/details/128974654

https://pytorch.org/docs/stable/nn.html

1. nn.L1Loss

1.1 公式

L1Loss: 计算预测 x和 目标y之间的平均绝对值误差MAE, 即L1损失：
$$loss=\frac{1}{n}\sum _{i=1,...n}|x_i-y_i|$$

1.2 语法

torch.nn.L1Loss(size_average=None, reduce=None, reduction='mean')

• size_average与reduce已经被弃用，具体功能可由reduction替代
• reduction：指定损失输出的形式，有三种选择：none|mean|sum。none：损失不做任何处理，直接输出一个数组；mean：将得到的损失求平均值再输出，会输出一个数；sum：将得到的损失求和再输出，会输出一个数

注意：输入的x 与y 可以是任意维数的数组，但是二者形状必须一致

1.3 应用案例

对比reduction不同时，输出损失的差异

import torch.nn as nn
import torch

x = torch.rand(10, dtype=torch.float)
y = torch.rand(10, dtype=torch.float)
L1_none = nn.L1Loss(reduction='none')
L1_mean = nn.L1Loss(reduction='mean')
L1_sum = nn.L1Loss(reduction='sum')
out_none = L1_none(x, y)
out_mean = L1_mean(x, y)
out_sum = L1_sum(x, y)
print(x)
print(y)
print(out_none)
print(out_mean)
print(out_sum)

2.nn.MSELoss

2.1 公式

MSELoss也叫L2 loss, 即计算预测x和目标y的平方误差损失。MSELoss的计算公式如下:

$$loss=\frac{1}{n}\sum _{i=1,..n}(x_i-y_i{)}^2$$

注:输入x 与y 可以是任意维数的数组，但是二者shape大小一致

2.2 函数定义

torch.nn.MSELoss(reduction = 'mean')

其中：

• reduction：指定损失输出的形式，有三种选择：none|mean|sum。none：损失不做任何处理，直接输出一个数组；mean：将得到的损失求平均值再输出，会输出一个数；sum：将得到的损失求和再输出，会输出一个数

2.3 应用案例

对比reduction不同时，输出损失的差异

import torch.nn as nn
import torch

x = torch.rand(10, dtype=torch.float)
y = torch.rand(10, dtype=torch.float)
mse_none = nn.MSELoss(reduction='none')
mse_mean = nn.MSELoss(reduction='mean')
mse_sum = nn.MSELoss(reduction='sum')
out_none = mse_none(x, y)
out_mean = mse_mean(x, y)
out_sum = mse_sum(x, y)


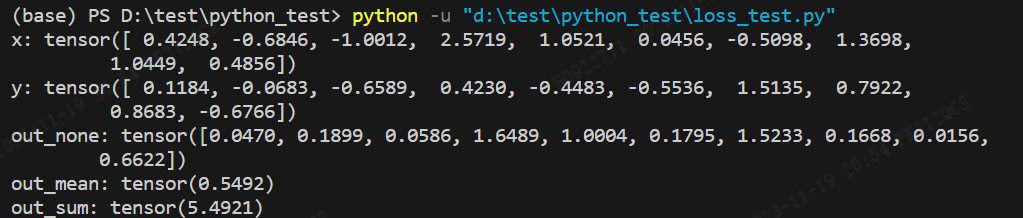
print('x:',x)
print('y:',y)
print("out_none:",out_none)
print("out_mean:",out_mean)
print("out_sum:",out_sum)

3 nn.SmoothL1Loss

3.1 公式

SmoothL1Loss是结合L1 loss和L2 loss改进的，其数学定义如下：

如果绝对值误差低于$\beta$, 则使用$L2$损失，，否则使用绝对值损失$L1$, ，此损失对异常值的敏感性低于$L2$ ，即当$x$与$y$相差过大时，该损失数值要小于$L2$损失，在某些情况下该损失可以防止梯度爆炸。

3.2 函数定义

torch.nn.SmoothL1Loss( reduction='mean', beta=1.0)

• reduction：指定损失输出的形式，有三种选择：none|mean|sum。none：损失不做任何处理，直接输出一个数组；mean：将得到的损失求平均值再输出，会输出一个数；sum：将得到的损失求和再输出，会输出一个数
• beta：损失在$L1$和$L2$之间切换的阈值，默认beta=1.0

3.3 应用案例

import torch.nn as nn
import torch

# reduction设为none便于逐元素对比损失值
loss_none = nn.SmoothL1Loss(reduction='none')
loss_sum = nn.SmoothL1Loss(reduction='sum')
loss_mean = nn.SmoothL1Loss(reduction='mean')
x = torch.randn(10)
y = torch.randn(10)
out_none = loss_none(x, y)
out_sum = loss_sum(x, y)
out_mean = loss_mean(x, y)
print('x:',x)
print('y:',y)
print("out_none:",out_none)
print("out_mean:",out_mean)
print("out_sum:",out_sum)

4. nn.CrossEntropyLoss

nn.CrossEntropyLoss 在pytorch中主要用于多分类问题的损失计算。

4.1 交叉熵定义

交叉熵主要是用来判定实际的输出与期望的输出的接近程度，也就是交叉熵的值越小，两个概率分布就越接近。
假设概率分布p为期望输出(target)，概率分布q为实际输出(pred), $H(p,q)$为交叉熵， 则：

Pytorch中的CrossEntropyLoss()函数

Pytorch中计算的交叉熵并不是采用交叉熵定义的公式得到的,其中q为预测值，p为target值：

而是交叉熵的另外一种方式计算得到的：

Pytorch中CrossEntropyLoss()函数的主要是将log_softmax 和NLLLoss（最小化负对数似然函数）合并到一块得到的结果

CrossEntropyLoss()=log_softmax() + NLLLoss() 

• (1) 首先对预测值pred进行softmax计算：其中softmax函数又称为归一化指数函数，它可以把一个多维向量压缩在(0,1)之间，并且它们的和为1
  
• (2) 然后对softmax计算的结果，再取log对数。
• (3) 最后再利用NLLLoss() 计算CrossEntropyLoss， 其中NLLLoss() 的计算过程为：将经过log_softmax计算的结果与target 相乘并求和，然后取反。

其中(1),(2)实现的是log_softmax计算，(3)实现的是NLLLoss(), 经过以上3步计算，得到最终的交叉熵损失的计算结果。

4.2 函数定义

torch.nn.CrossEntropyLoss(weight=None,size_average=None,ignore_index=-100,reduce=None,reduction='mean',label_smoothing=0.0)

• 最常用的参数为 reduction(str, optional) ，可设置其值为 mean, sum, none ，默认为 mean。该参数主要影响多个样本输入时，损失的综合方法。mean表示损失为多个样本的平均值，sum表示损失的和，none表示不综合。
• weight: 可手动设置每个类别的权重，weight的数组大小和类别数需保持一致

4.3 应用案例

import torch.nn as nn
import torch
loss_func = nn.CrossEntropyLoss()
pre = torch.tensor([[0.8, 0.5, 0.2, 0.5]], dtype=torch.float)
tgt = torch.tensor([[1, 0, 0, 0]], dtype=torch.float)
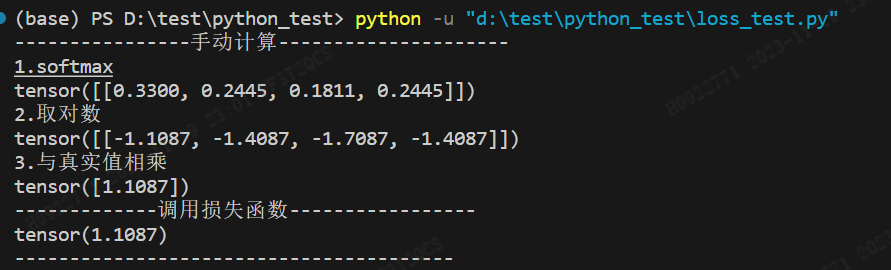
print('----------------手动计算---------------------')
print("1.softmax")
print(torch.softmax(pre, dim=-1))
print("2.取对数")
print(torch.log(torch.softmax(pre, dim=-1)))
print("3.与真实值相乘")
print(-torch.sum(torch.mul(torch.log(torch.softmax(pre, dim=-1)), tgt), dim=-1))
print('-------------调用损失函数-----------------')
print(loss_func(pre, tgt))
print('----------------------------------------')

由此可见：

• ①交叉熵损失函数会自动对输入模型的预测值进行softmax。因此在多分类问题中，如果使用nn.CrossEntropyLoss()，则预测模型的输出层无需添加softmax层。

• ②nn.CrossEntropyLoss()=nn.LogSoftmax()+nn.NLLLoss().

nn.CrossEntropyLoss() 的target可以是one-hot格式，也可以直接输出类别，不需要进行one-hot处理，如下示例:

import torch
import torch.nn as nn
x_input=torch.randn(3,3)#随机生成输入 
print('x_input:\n',x_input) 
y_target=torch.tensor([1,2,0])#设置输出具体值 print('y_target\n',y_target)

#计算输入softmax，此时可以看到每一行加到一起结果都是1
softmax_func=nn.Softmax(dim=1)
soft_output=softmax_func(x_input)
print('soft_output:\n',soft_output)

#在softmax的基础上取log
log_output=torch.log(soft_output)
print('log_output:\n',log_output)

#对比softmax与log的结合与nn.LogSoftmaxloss(负对数似然损失)的输出结果，发现两者是一致的。
logsoftmax_func=nn.LogSoftmax(dim=1)
logsoftmax_output=logsoftmax_func(x_input)
print('logsoftmax_output:\n',logsoftmax_output)

#pytorch中关于NLLLoss的默认参数配置为：reducetion=True、size_average=True
nllloss_func=nn.NLLLoss()
nlloss_output=nllloss_func(logsoftmax_output,y_target)
print('nlloss_output:\n',nlloss_output)

#直接使用pytorch中的loss_func=nn.CrossEntropyLoss()看与经过NLLLoss的计算是不是一样
crossentropyloss=nn.CrossEntropyLoss()
crossentropyloss_output=crossentropyloss(x_input,y_target)
print('crossentropyloss_output:\n',crossentropyloss_output)

• 其中pred为x_input=torch.randn(3,3，对应的target为y_target=torch.tensor([1,2,0]), target并没有处理为one-hot格式，也可以正常计算结果的。pytorch中图像的标签编号为标量：0、1 、2 … C-1，输入到损失函数不需要变成one-hot向量（pytorch可自动去做）

5. nn.BCELoss

nn.BCELoss() 是 二元交叉熵损失函数 （Binary Cross Entropy Loss）

• 适i用于二分类问题，即
  • 模型的输出为一个概率值，表示样本属于某一类的概率
  • 标签为二元值：0 或 1
• nn.BCELoss() 计算的是二元交叉熵损失，也称为对数损失，它将模型 预测值 和 真实标签值 之间的差异转化为一个标量损失值，用于衡量模型预测的准确性。

5.1 公式

$$L=-\frac{1}{N}\sum _{i=1}^N{w}_i[y_{i}log(\widehat{y_i})+(1-y_i)log(1-\widehat{y_i})]$$
其中:

• N : 表示一个Batch的样本数量
• $y_i$:表示第$i$个样本的实际标签
• $\widehat{y_i}$:表示第i个样本的实际预测值
• $w_i$: 表示batch中第i个样本的权重

5.2 函数定义

torch.nn.BCELoss(weight=None, size_average=None, reduce=None, reduction='mean')

• size_average和reduce已经被弃用，具体功能可由reduction替代
• reduction：指定损失输出的形式，有三种选择：none|mean|sum。none：损失不做任何处理，直接输出一个数组；mean：将得到的损失求平均值再输出，会输出一个数；sum：将得到的损失求和再输出，会输出一个数
• weight: 用于对每个样本的损失值进行加权。默认值为 None

5.3 应用案例

import torch.nn as nn  
import torch  
import numpy as np  

loss_fn = nn.BCELoss()

class MLP(nn.Module):
    '''自己定义网络的层,要继承nn.Module'''
    def __init__(self):
        super().__init__()
        self.Lin = nn.Linear(in_features=2, out_features=1)
        self.Sig = nn.Sigmoid()
        
    def forward(self, x):
        '''定义前向过程,输出shape为(batch,)'''
        logit = self.Lin(x)
        y_pred = self.Sig(logit)
        return y_pred 

X = torch.FloatTensor(np.array([[1,2],[3,4],[5,6]]))
y = torch.FloatTensor(np.array([[0],[1],[0]])) #shape=(batch,1)，并且是float32
model = MLP()
y_pred = model(X)
loss = loss_fn(y_pred,y) #


print('y_pred的数值：')
print(y_pred)
print()
#print('loss的数值：一般默认把一整batch的样本的loss取平均值，所以是标量')
print(loss)

注意:

• 使用nn.BCELoss()损失时， 模型的输出需要再经过sigmoid处理，然后与标签一起送入到nn.BCELoss()中计算损失loss，因为nn.BCELoss() 函数本身内部没有sigmoid处理。
• 而nn.BCEWithLogitsLoss函数内部会进行sigmoid处理，所以模型输出直接和标签送到loss计算即可，不需要再经过sigmoid处理。

6. nn.BCEWithLogitsLoss

• nn.BCEWithLogitsLoss() 通常用于二分类任务, 将模型的输出通过BCEWithLogitsLoss() 内部的 Sigmoid 函数处理，将其转换为一个在0到1之间的概率值。然后，它计算模型输出与目标标签之间的二元交叉熵损失。
• 需要注意的是，nn.BCEWithLogitsLoss() 可以用于多标签分类任务， 其中每个样本可以属于多个类别，因为它用的是sigmoid处理，而不像rossEntropyLoss()使用的是softmax。在这种情况下，每个类别被视为一个独立的二分类问题，并且损失通过对每个类别计算二元交叉熵的平均值得到。
• torch.nn.BCEWithLogitsLoss()还支持设置 pos_weight 参数，用于处理样本不平衡的问题。而 nn.BCELoss() 不支持设置 pos_weight 参数。

nn.BCEWithLogitsLoss与nn.BCELoss的不同

• BCELoss一般和sigmoid 一起用，神经网络需要经过sigmoid函数
• nn.BCEWithLogitsLoss包括了 Sigmoid 层和BCELoss 层，故而神经网络的输出无需经过sigmoid函数，其他都是一样的。

nn.BCEWithLogitsLoss与CrossEntorpy的不同

• CrossEntorpy使用softmax函数，即将模型输出值作为softmax函数的输入，进而计算样本属于每个类别的概率，softmax计算得到的类别概率值加和为1。
• BCEWithLogitsLoss使用sigmoid函数，将模型输出值作为sigmoid函数的输入，计算得到的多个类别概率值加和不一定为1
• 在二分类、多分类任务中通常使用交叉熵损失函数，即Pytorch中的CrossEntorpy或BCEWithLogitsLoss，但是在多标签分类任务中使用的是BCEWithLogitsLoss函数。

6.1 公式

• torch.nn.BCEWithLogitsLoss() 的输入是也是 二元分类模型的输出值$z$和实际标签$y$, 不同的是$z$ 在模型内部没有经过 sigmoid 处理,是任意实数。这种情况下，sigmoid处理就被放到了损失函数中，所以，torch.nn.BCEWithLogitsLoss() 函数内部的计算过程是先对$z$应用 sigmoid 函数，将其映射到 [0,1] 范围内，然后使用二元交叉熵计算预测值和实际标签之间的损失值。

• 另外，torch.nn.BCEWithLogitsLoss() 还支持设置 pos_weight 参数，用于处理样本不平衡的问题。而 nn.BCELoss() 不支持设置 pos_weight 参数。

6.2 函数定义

torch.nn.BCEWithLogitsLoss(weight=None, size_average=None,  reduce=None,  reduction='mean',  pos_weight=None)

• reduction：指定如何对每个 batch 的损失值进行降维。可选值为 ‘none’、‘mean’ 和 ‘sum’。默认值为 ‘mean’。
• pos_weight：用于对正样本的损失值进行加权。可以用于处理样本不平衡的问题。例如，如果正样本比负样本少很多，可以设置 pos_weight 为一个较大的值，以提高正样本的权重。默认值为 None。

6.3 应用案例

案例1：

import torch
import torch.nn as nn

#创建输入
input = torch.tensor([[0.1,0.2,0.3],[0.4,0.5,0.6]])#共有两个输入样本
label_onehot = torch.FloatTensor([[0, 1,0], [1,0,1]])  # onehot编码格式


#创建模型并计算
model = nn.Linear(in_features=3,out_features=3)#此处随便写一个模型示意
model_out = model(input)

#计算损失函数值
log_bce_loss = torch.nn.BCEWithLogitsLoss()
loss_onehot =log_bce_loss(model_out,label_onehot)


print("BCEWithLogitsLoss-onehot",loss_onehot)

案例2

import torch
import torch.nn as nn
import numpy as np
loss_fn = nn.BCEWithLogitsLoss()
class MLP(nn.Module):
    '''自己定义网络的层,要继承nn.Module'''
    def __init__(self):
        super().__init__()
        self.Lin = nn.Linear(in_features=2, out_features=1)
        
    def forward(self, x):
        '''定义前向过程,输出shape为(batch,)'''
        logit = self.Lin(x)
        return logit #区别就在这里啦'''

X = torch.FloatTensor(np.array([[1,2],[3,4],[5,6]]))
y = torch.FloatTensor(np.array([[0],[1],[2]])) #shape=(batch,1)，并且是float32
model = MLP()
y_pred = model(X)
loss = loss_fn(y_pred,y) #

print("loss:",loss)