Matlab群体智能优化算法之海象优化算法(WO)
文章目录
- 一、灵感来源
- 二、算法的初始化
- 三、GTO的数学模型
- Phase1:危险信号和安全信号
- Phase2:迁移(探索)
- Phase3:繁殖(开发)
- 四、流程图
- 五、伪代码
- 六、算法复杂度
- 七、WO搜索示意图
- 八、实验分析和结果
- 23个常见的基础测试函数
- CEC2021测试函数
- 实际工程优化问题
Walrus optimizer: A novel nature-inspired metaheuristic algorithm
Walrus optimizer: A novel nature-inspired metaheuristic algorithm
摘要:该文献Introduction介绍了为什么做这个元启发式算法的原因;Related works列举了2021-2023年一些算法。我将按照自己理解完全复现这篇文章,包括理论介绍、完整的实验部分。个人能力有限,如有不足,还请见谅。参考文献:Han M, Du Z, Yuen K, et al. Walrus Optimizer: A novel nature-inspired metaheuristic algorithm[J]. Expert Systems with Applications, 2023: 122413.
注:仅记录学习,如有侵权,联系删除。
- 1、所写内容只是个人理解,如有错误,还请包涵
- 2、所用主题为slandarer提供的墨滴模板
- 3、CSDN:勉为其难免免
- 4、微信公众号:飘散在人间的一缕青丝
一、灵感来源
海象是海洋中除鲸鱼外最大的哺乳动物。海象主要生活在北极或附近的温带水域,海象是群居动物,过着两栖生活。海象群的数量从几十到几百到几千不等。它的身体是圆柱形的,粗壮而肥胖,头部扁平,枪口末端钝。在上唇周围有大约400根长而硬的胡须,带有血管和神经,导致触觉敏锐。海象最独特的特征是那对白色、发育良好的上犬齿,它们在其一生中不断生长,形成象牙。象牙可用于自卫,在泥沙中挖掘蛤蜊、虾和螃蟹等食物,或在冰上攀爬时支撑身体。
海象庞大的身体看起来很笨重,但在水中很灵活。在众多的海洋动物中,海象是最好的潜水员。他们可以在水中潜水 20 分钟,深度为 500 m。海象潜入海底后可以在水下停留长达 2 小时,一旦需要新鲜空气,它们可以在 3 分钟内浮出水面。
海象具有很强的社区意识,如下所示:
(1)、当繁殖季节开始时,海象会在海滩上建立自己的领地。最好的位置被最强壮的男性占据。领土的面积根据男性占据的女性数量而变化。
(2)、海象习惯于生活在阳光无法到达的海洋深水区。像蝙蝠和海豚一样,海象缺乏独特的视力;它们依靠合理的定位进行觅食,并通过与同龄人交流来共享食物信息。
(3)、海象有很强的社交习惯,当它们在水中遇到虎鲸时,它们会采取集体防御策略来保护自己并帮助受伤的虎鲸。长期的生存斗争经验使海象无法放松警惕。在这一点上,两只海象充当警卫。一旦他们的同类受伤,他们就会去帮忙。
受海象迁徙、繁殖、栖息和觅食行为的启发(如图1所示),我们首次提出了一种新的元启发式算法WO算法。这里需要澄清两个假设:
(1)、海象种群通过危险和安全信号来判断种群行为。
(2)、海象种群的行为和角色划分在海象算法中建模。具体来说,海象算法假设雄性、雌性和幼年海象之间的社会结构和相互作用。
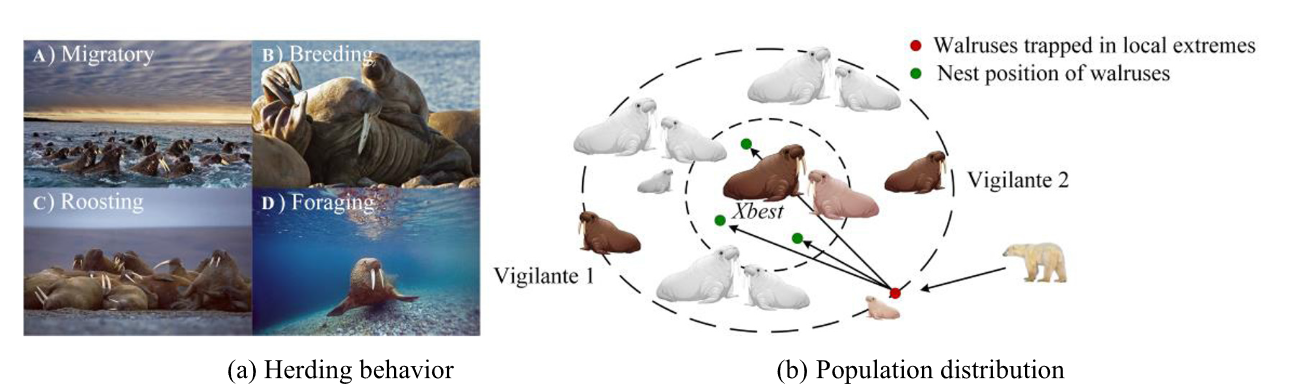
创新之处在于,海象群中的“义警”是影响象群方向的决定性因素。“治安队员”发出的[危险信号]及[安全信号],在[行动计划]的执行过程中起着关键作用。在WO中,“危险信号”用于确定WO是执行勘探阶段还是开发阶段。当“危险信号”满足一定条件时,海象群迁移到解空间内的新域,这是算法早期阶段的探索阶段。相反,海象群繁殖,这是算法后期的开发阶段。“安全信号”在开发阶段起着关键作用,它影响着海象是选择栖息行为还是觅食。其中,雄性海象、雌性海象和幼年海象在栖息行为中相互作用,使种群朝着有利于生存的方向移动;觅食行为包括典型的聚集和逃跑现象,这些现象由“危险信号”控制。在有序的警务环境中,海象群可以避免被捕食者捕获或死亡(落入局部最佳状态),并实现种群增长(寻找全局最佳状态)。
二、算法的初始化
X代表WO种群矩阵,
X
i
=
(
x
i
,
1
,
x
i
,
2
,
.
.
.
,
x
i
,
m
)
X_{i}=(x_{i,1},x_{i,2},...,x_{i,m})
Xi=(xi,1,xi,2,...,xi,m)是WO的第i个成员(候选解)。
F代表适应度函数值。
X
=
[
X
1
⋮
X
i
⋮
X
N
]
N
×
m
=
[
x
1
,
1
⋯
x
1
,
j
⋯
x
1
,
m
⋮
⋱
⋮
⋮
x
i
,
1
⋯
x
i
,
j
⋯
x
i
,
m
⋮
⋮
⋱
⋮
x
N
,
1
⋯
x
N
,
j
⋯
x
N
,
m
]
N
×
m
X=\left[\begin{array}{c} X_{1} \\ \vdots \\ X_{i} \\ \vdots \\ X_{N} \end{array}\right]_{N \times m}=\left[\begin{array}{ccccc} x_{1,1} & \cdots & x_{1, j} & \cdots & x_{1, m} \\ \vdots & \ddots & \vdots & & \vdots \\ x_{i, 1} & \cdots & x_{i, j} & \cdots & x_{i, m} \\ \vdots & & \vdots & \ddots & \vdots \\ x_{N, 1} & \cdots & x_{N, j} & \cdots & x_{N, m} \end{array}\right]_{N \times m}
X=
X1⋮Xi⋮XN
N×m=
x1,1⋮xi,1⋮xN,1⋯⋱⋯⋯x1,j⋮xi,j⋮xN,j⋯⋯⋱⋯x1,m⋮xi,m⋮xN,m
N×m
x
i
,
j
=
l
b
j
+
rand
⋅
(
u
b
j
−
l
b
j
)
,
i
=
1
,
2
,
…
,
N
,
j
=
1
,
2
,
…
,
m
x_{i, j}=lb_{j}+\text { rand } \cdot\left(ub_{j}-lb_{j}\right), i=1,2, \ldots, N, j=1,2, \ldots, m
xi,j=lbj+ rand ⋅(ubj−lbj),i=1,2,…,N,j=1,2,…,m
F
=
[
F
1
⋮
F
i
⋮
F
N
]
N
×
1
=
[
F
(
X
1
)
⋮
F
(
X
i
)
⋮
F
(
X
N
)
]
N
×
1
F=\left[\begin{array}{c} F_{1} \\ \vdots \\ F_{i} \\ \vdots \\ F_{N} \end{array}\right]_{N \times 1}=\left[\begin{array}{c} F\left(X_{1}\right) \\ \vdots \\ F\left(X_{i}\right) \\ \vdots \\ F\left(X_{N}\right) \end{array}\right]_{N \times 1}
F=
F1⋮Fi⋮FN
N×1=
F(X1)⋮F(Xi)⋮F(XN)
N×1
式中: x i , j x_{i, j} xi,j代表第i个成员的第j个变量的值;N是种群大小;m是维度;rand代表[0,1]之间的随机数; l b j lb_{ j} lbj代表下限; u b j ub_{ j} ubj代表上限。
三、GTO的数学模型
海象种群分为成年和幼体,分别占种群的90%和10%。在成年海象中,雄性与雌性的比例为1:1。
Phase1:危险信号和安全信号
海象在觅食和栖息时都非常警惕。会有1至2只海象作为警卫在周围巡逻,一旦发现意外情况,会立即发出危险信号。其中危险信号和安全信号定义如下:
Dangersignal = A ∗ R α = 1 − t / T A = 2 × α R = 2 × r 1 − 1 \begin{aligned} & \text { Dangersignal }=A^* R \\ & \alpha=1-t / T \\ & A=2 \times \alpha \\ & R=2 \times r_1-1 \end{aligned} Dangersignal =A∗Rα=1−t/TA=2×αR=2×r1−1
其中 A A A和 R R R是危险因子, α \alpha α随着迭代次数的增加,从1减小到0。 Levy ( Dim ) \text { Levy }(\text { Dim }) Levy ( Dim )是Levy飞行, T T T是最大迭代次数。
WO中危险信号对应的安全信号定义如下:
Safetysignal
=
r
2
\begin{aligned} & \text { Safetysignal }=r_2 \\ \end{aligned}
Safetysignal =r2
其中
r
1
r_1
r1和
r
2
r_2
r2是在[0,1]内的随机数。
Phase2:迁移(探索)
当危险因子过高时,海象群会迁移到更适合种群生存的地区。在此阶段,海象位置更新如下:
X
i
,
j
t
+
1
=
X
i
,
j
t
+
Migrationstep
X_{i, j}^{t+1}=X_{i, j}^t+\text { Migrationstep }
Xi,jt+1=Xi,jt+ Migrationstep
Migrationstep
=
(
X
m
t
−
X
n
t
)
∙
β
∙
r
3
2
\text { Migrationstep } =\left(X_m^t-X_n^t\right) \bullet \beta \bullet r_3{ }^2
Migrationstep =(Xmt−Xnt)∙β∙r32
β
=
1
−
1
1
+
exp
(
−
t
−
T
2
T
×
10
)
\beta=1-\frac{1}{1+\exp \left(-\frac{t-\frac{T}{2}}{T} \times 10\right)}
β=1−1+exp(−Tt−2T×10)1
其中
X
i
,
j
t
+
1
X_{i, j}^{t+1}
Xi,jt+1是i个个体在第j个维度上的更新位置,
X
i
,
j
t
X_{i, j}^{t}
Xi,jt是当前位置,Migration_step是海象运动的步长,从种群中随机选择两个警惕者,其位置对应于
X
m
t
X_m^t
Xmt和
X
m
n
X_m^n
Xmn,
β
\beta
β是迁移步长控制因子,它随着迭代变化为平滑曲线,
r
3
r_3
r3是在[0,1]内的随机数。
Phase3:繁殖(开发)
与迁徙相反,当风险因素较低时,海象群倾向于在洋流中繁殖。在繁殖过程中,主要有两种行为,陆上栖息和水下觅食。数学模型如下。
(1)栖息行为
雄性、雌性和幼年海象是我们对种群成员的分类。他们有不同的方式来更新他们的立场。
第 1 步:雄性海象的重新分布
采用Halton序列分布进行雄性海象位置更新,可以扩大种群的搜索分布
第 2 步:更新雌性海象的位置
雌性海象受到雄性海象 Male i , j t \text { Male }_{i, j}^t Male i,jt和领头海象 X best t X_{\text {best }}^t Xbest t的影响。随着迭代过程的进行,雌性海象逐渐减少对配偶的影响,而更多地受到领导者的影响。
Female i , j t + 1 = Female i , j t + α ∙ ( Male i , j t − Female i , j t ) + ( 1 − α ) ∙ ( X best t − Female i , j t ) \begin{aligned} \text { Female }_{i, j}^{t+1}= & \text { Female }_{i, j}^t+\alpha \bullet\left(\text { Male }_{i, j}^t-\text { Female }_{i, j}^t\right)+(1-\alpha) \\ & \bullet\left(X_{\text {best }}^t-\text { Female }_{i, j}^t\right) \end{aligned} Female i,jt+1= Female i,jt+α∙( Male i,jt− Female i,jt)+(1−α)∙(Xbest t− Female i,jt)
第 3 步:更新幼年海象的位置
种群边缘的幼年海象经常成为虎鲸和北极熊的目标。因此,幼年海象需要更新其当前位置以避免捕食。
Juvenile i , j t + 1 = ( O − Juvenile i , j t ) ∙ P O = X best t + Juvenile i , j t ∙ L F \begin{aligned} & \text { Juvenile }_{i, j}^{t+1}=\left(O-\text { Juvenile }_{i, j}^t\right) \bullet P \\ & O=X_{\text {best }}^t+\text { Juvenile }_{i, j}^t \bullet L F \end{aligned} Juvenile i,jt+1=(O− Juvenile i,jt)∙PO=Xbest t+ Juvenile i,jt∙LF
P是幼年海象的遇险系数,是[0,1]的随机数,O是参考安全位置,LF是基于 L ́evy分布的随机数向量,表示Levy运动。
Levy ( a ) = 0.05 × x ∣ y ∣ 1 a σ x = [ Γ ( 1 + α ) sin ( π α 2 ) Γ ( 1 + α 2 ) α 2 ( α − 1 ) 2 ] 1 α , σ y = 1 , α = 1.5 \begin{gathered} \operatorname{Levy}(a)=0.05 \times \frac{x}{|y|^{\frac{1}{a}}} \\ \sigma_x=\left[\frac{\Gamma(1+\alpha) \sin \left(\frac{\pi \alpha}{2}\right)}{\Gamma\left(\frac{1+\alpha}{2}\right) \alpha 2^{\frac{(\alpha-1)}{2}}}\right]^{\frac{1}{\alpha}}, \sigma_y=1, \alpha=1.5 \end{gathered} Levy(a)=0.05×∣y∣a1xσx=[Γ(21+α)α22(α−1)Γ(1+α)sin(2πα)]α1,σy=1,α=1.5
其中,其中x和y是两个正态分布变量, x N ( 0 , σ x 2 ) x \mathrm{~N}\left(0, \sigma_x^2\right) x N(0,σx2), y N ( 0 , σ x 2 ) y \mathrm{~N}\left(0, \sigma_x^2\right) y N(0,σx2) 。 σ x \sigma_x σx 和 σ y \sigma_y σy是标准差, Γ ( x ) = ( x + 1 ) ! \Gamma(x)=(x+1) ! Γ(x)=(x+1)!
(2)觅食行为
水下觅食包括逃跑和采集行为
a) 逃跑行为
海象在水下觅食时也会受到天敌的攻击,它们会根据同伴发出的危险信号逃离当前的活动区域。这种行为发生在WO的后期迭代中,对种群的一定程度的扰动有助于海象进行全局探索。
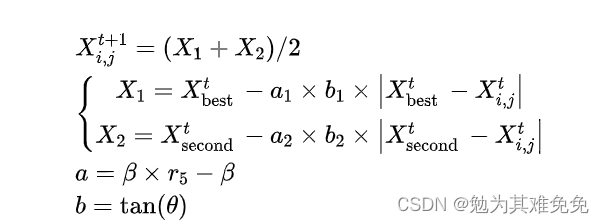
其中, X 1 X_1 X1和 X 2 X_2 X2是影响海象聚集行为的两个权重, X second t X_{\text {second }}^t Xsecond t是第二只海象在当前迭代中的位置, ∣ X second t − X i , j t ∣ \left|X_{\text {second }}^t-X_{i, j}^t\right| Xsecond t−Xi,jt 表示当前海象与第二只海象之间的距离,a和b为聚集系数, r 5 r_5 r5为随机数,位于[0,1], θ \theta θ取的值范围为0到π。
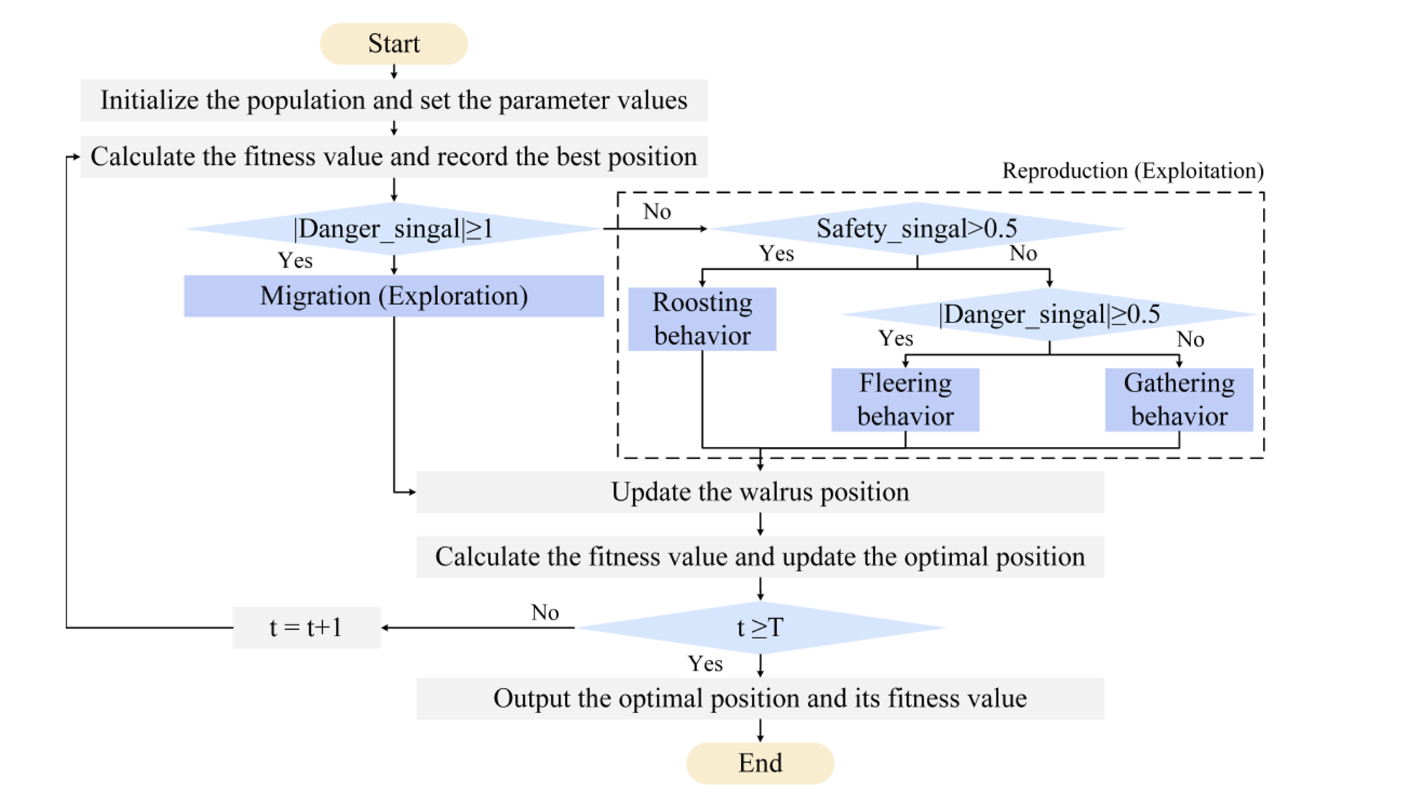
四、流程图
在WO中,危险信号用于确定WO是执行勘探阶段还是开发阶段。当危险信号绝对值不小于1时,海象群迁移到解空间内的新域,即算法早期的探索阶段;相反,海象群繁殖,这是算法后期的开发阶段。安全信号在开发阶段起着关键作用,它影响着个体海象是选择栖息行为还是觅食行为。其中,觅食行为包括聚集和逃跑两种典型现象,它们受危险信号的控制。
五、伪代码

六、算法复杂度
在求解优化问题时,计算复杂度对于评估算法的效率非常有用,它取决于三个主要过程:初始化、适应度评估和解决方案的更新。初始化过程和更新机制的计算复杂度分别为O(N)和O(N × T)+ O(N × T × D),其中N为种群大小,T为最大迭代次数,D为给定问题的维数。因此,WO的计算复杂度为O(N ×( T +T × D +1))。算法在运行过程中临时占用的内存空间量可以用空间复杂度来衡量。WO算法的空间复杂度是在其初始化过程中考虑的任何时间使用的最大空间量。因此,WO算法的空间复杂度为 O(N × Dim)。
七、WO搜索示意图
为了可视化所提出的算法的行为,本节显示了海象群行为的模拟。下图描绘了30个海象在三维空间中寻找单峰和多峰函数最优解的群体行为。红点表示全局最佳位置,其余为海象位置。当t=1时,海象在解空间中随机生成,散射范围较宽。随着迭代的继续,所有海象的搜索范围逐渐缩小。最后,所有海象都汇聚到红点上。单模态函数的搜索结果可以表明WO具有较好的开发能力,多模态函数的搜索结果可以反映WO较强的探索能力。(注:与文献中稍有不同的是我加了一个原函数图像,Sphere就是常见的测试函数F1,Rastrigin函数是F9,直接修改序号即可)



八、实验分析和结果
写了很久笔记了,也没有写完整的实验。在这篇中,完整的复现一下。包括多次独立运行、对数据的统计、导入到excel、出图,锻炼一下,顺便缝缝补补自己以前的烂代码。整体的思路就按照这篇论文的来写吧。后续看到好看的图再补充吧。
为了适当验证WO算法的性能,原作者进行了大量实验。
23个常见的基础测试函数
1、定性分析
使用几种单峰和多模态标准准则函数对WO的定性结果进行评估,并使用WO的4个不同标准对结果进行评估,包括搜索历史、第一智能体的轨迹、平均拟合度和收敛曲线。搜索历史图显示了海象个体在迭代期间访问的所有位置;轨迹图监控第一只海象在迭代过程中的变化情况;平均适应度图显示了海象种群的整体变化;收敛行为图记录了总体每次迭代后的最佳解。
从23个基准测试中选出10个典型函数进行分析。从搜索历史可以看出,WO在处理不同情况时,包括促进多样化、探索解决方案空间的有利区域、开发最优位置邻域等,都呈现出相似的模式。(一旦涉及了位置绘图可视化,要么每个测试问题的维度设置为2,要么就是画图的时候选择前两个位置。在此我选择第二种方法)
种群大小设置为30,迭代次数设置为400。从23个里面选择了十个来进行分析。
%% 定性分析23个基准测试函数
clear
clc
close all
populationSize = 30;
Max_iteration = 400;
selet_fcn = [1,3,7,8,10,12,14,15,18,21];
for i=1:length(selet_fcn)-5
fn = 1;
Function_name=strcat('F',num2str(selet_fcn(i)));
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
% dim = 2;
% rng('shuffle');%根据当前时间初始化生成器,在每次调用 rng 后会产生一个不同的随机数序列。
[Best_score,Best_pos,PO_cg_curve,All_Pos,fitness1st,fitnessallmean]=WO3(populationSize,Max_iteration,lb,ub,dim,fobj);
%% 绘制定性分析图
figure('NumberTitle','off','Color','w','Name','函数图像','Units','centimeters','Position',[4,15,40,7])
tiledlayout(1,5);
nexttile
%绘制原图像
fun_plot(Function_name)
nexttile
%搜索历史图
fun_plot(Function_name);
h = gca;
h.Children(2).Visible = "off";
hold on
view(0,90)
for i = 1:length(All_Pos)
temp = All_Pos{i};
scatter(temp(:,1),temp(:,2),12,'k')
end
title('Search history')
box on
grid on
nexttile
plot(fitness1st,'Color',[6, 253, 244]./255,'LineWidth',1.5)
title('Trajectory in 1st agents')
box on
grid on
nexttile
plot(fitnessallmean,'Color',[28, 29, 252]./255,'LineWidth',1.5)
title('average fitness of all agents')
box on
grid on
nexttile
semilogx(PO_cg_curve,'Color',[245, 42, 237]./255,'LineWidth',1.5)
title('Convergence curve')
box on
grid on
end










关于图搜索历史和第一智能体的迹和原文不一样,理解不到位。暂时先这样放着,待后续理解更透彻了再修改这个图。其实这个每跑一次产生的图都不一样,感兴趣的可以多跑几次试试。
2、定量分析
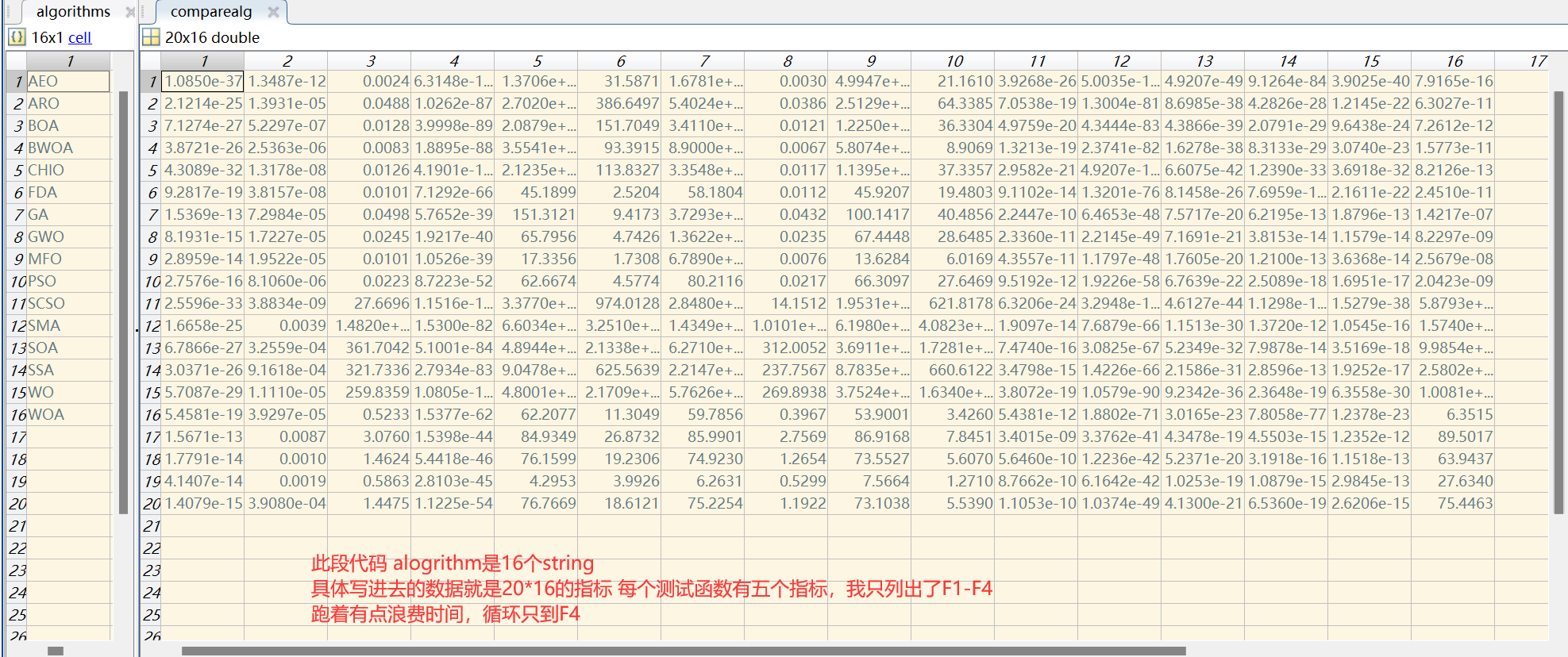
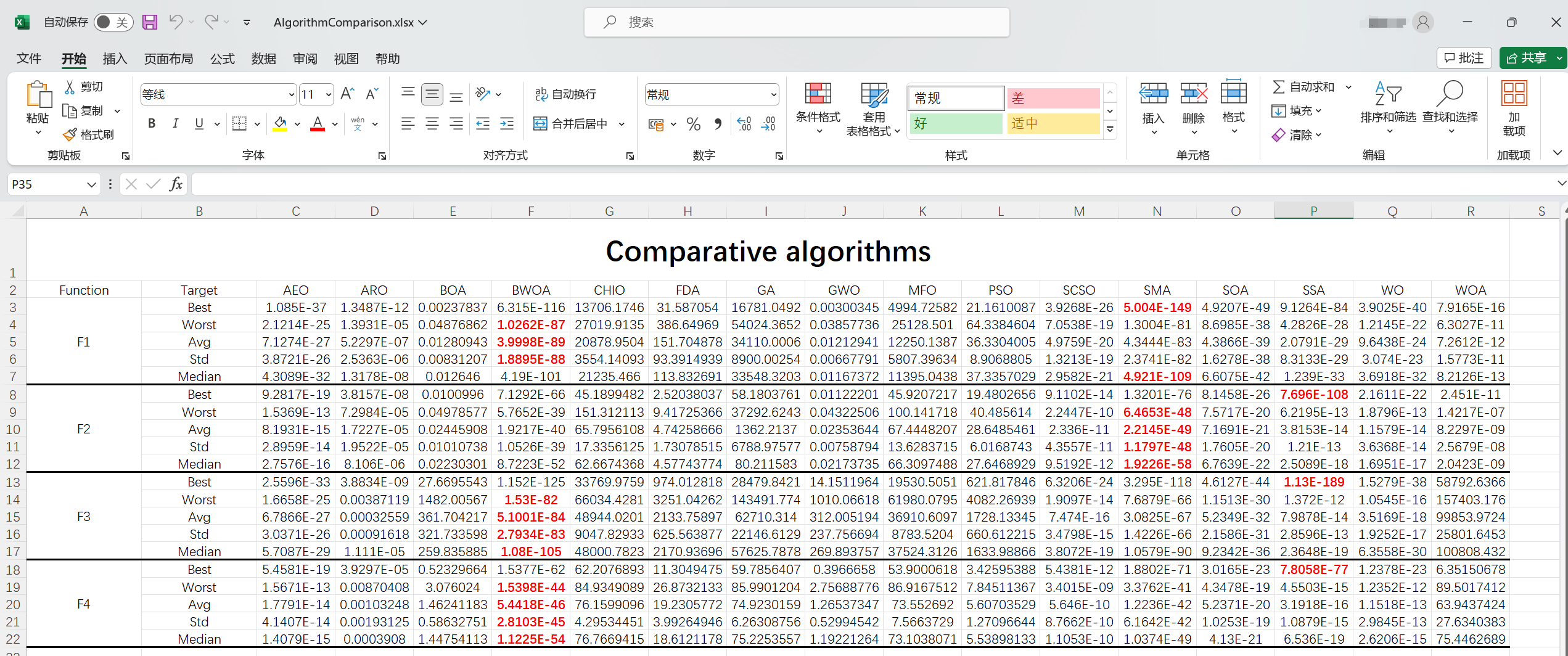
这部分仿真时,文中未明确说明种群大小和迭代次数,在此我设置种群大小为30,迭代次数为100。文中所提及的ABC、AOS、ChoA、FOA、SHO算法我暂时没有,在此我换四个其他算法,AEO、ARO、CHIO、FDA、SMA。为了节约时间,我独立运行了30次,并调用excel的com服务器将结果写在了excel表中。在此列出前四个函数的表格。对每一行的最小值进行的字体加粗,颜色设置为红色的处理。
%% 存储多个算法对比数据 平均值 最优值 最差值 中位数 标准差
clc
clear
close all
%% 加载实验数据
load 20231107_30_100_30_16_PM.mat
file_path=[pwd,'\AlgorithmComparison.xlsx'];%设置当前路径
try
excelApp=actxGetRunningServer('Excel.Application');%如果Excel 服务器已经打开,返回其句柄
catch
excelApp=actxserver('Excel.Application');%如果Excel服务器没有打开,则创建一个Excel服务器,并返回句柄
end
excelApp.Visible = true; % 使 Excel 可见
%% 添加一个新的工作簿
%如果存在test.xlsx文件,则打开文件,若不存在则创建一个,然后保存
if exist(file_path,'file')
workbook=excelApp.Workbooks.Open(file_path);%打开 注意这里打开的必须是绝对路径
else
workbook=excelApp.Workbooks.Add;%创建 创建工作簿的时候默认是1 在excel选项中设置
workbook.SaveAs(file_path)%保存
end
%% 使用默认的工作表
sheet = workbook.Sheets.Item(1);
%% 设置工作表的名称
sheet.Name = 'Algorithm Comparison';
%% 合并单元格并设置 "Comparative algorithms" 标题
% 假设总共有12个算法名称加上'Function'和'target'列,因此共14列
titleRange = sheet.Range('A1:R1'); % 直接指定从A1到N1的范围
titleRange.MergeCells = true;
titleRange.Value = 'Comparative algorithms';
titleRange.HorizontalAlignment = -4108;%使用 xlCenter 的数值
titleRange.Font.Bold = true;
titleRange.RowHeight = 50;
titleRange.Font.Size = 24;
% 填充算法名称 从加载的数据中读取
for i = 1:length(algorithms)
temp = strsplit(algorithms{i},'.');
algorithms(i)=temp(1);
end
% algorithms = {'AEO', 'ACO', 'SSA', 'SSA', 'SSA', 'SSA', 'SSA', 'SSA', 'SSA', 'SSA', 'SSA', 'SSA'};
% 从第三列开始填充算法名称
for i = 1:length(algorithms)
% 使用Excel列字母可以使得引用更加清晰
colLetter = char('B' + i); % 因为算法从第三列开始,所以是 'B' + i
rangeStr = sprintf('%s2', colLetter); % 生成范围字符串,如 'C2', 'D2', 等
sheet.Range(rangeStr).Value = algorithms{i};
end
%% 假设有以下函数和指标
functions = {'F1', 'F2', 'F3', 'F4'};
metrics = {'Best', 'Worst', 'Avg', 'Std', 'Median'};
% 为函数名、指标和随机数据填充表格
% 为函数名、指标和随机数据填充表格
for i = 1:length(functions)
% 合并相同函数名的单元格
startRow = (i-1)*length(metrics)+3; % 函数开始的行号
endRow = startRow + length(metrics) - 1; % 函数结束的行号
mergeRangeStr = sprintf('A%d:A%d', startRow, endRow);
mergeRange = sheet.Range(mergeRangeStr);
mergeRange.MergeCells = true;
mergeRange.Value = functions{i};
mergeRange.VerticalAlignment = -4108; % 垂直居中
mergeRange.HorizontalAlignment = -4108; % 水平居中
% 为每个指标生成并填充随机数据
for j = 1:length(metrics)
metricCell = sprintf('B%d', (i-1)*length(metrics)+j+2);
sheet.Range(metricCell).Value = metrics{j};
% 为每个指标的算法生成并填充随机数据
% for k = 1:length(algorithms)
% dataCell = sprintf('%s%d', char('B' + k), (i-1)*length(metrics)+j+2);
% sheet.Range(dataCell).Value = rand();
% end
end
end
sheet.Range('A2').Value = 'Function';
sheet.Range('B2').Value = 'Target';
% 调整列宽
% 调整第一列和第二列的列宽
sheet.Range('A:A').ColumnWidth = 15;
sheet.Range('B:B').ColumnWidth = 15;
% 假设算法从第三列开始,一共有12个算法
% 调整算法列的列宽
for i = 3:(2+length(algorithms))
colLetter = char('A' + i - 1); % 将列号转换为列字母
sheet.Range([colLetter ':' colLetter]).ColumnWidth = 10;
end
%% 获取用过的范围(整个数据区域)
usedRange = sheet.UsedRange;
% 你现在可以对这个范围进行操作,比如设置单元格的格式
% 设置整个区域的单元格内容居中对齐
usedRange.HorizontalAlignment = -4108; % 水平居中
usedRange.VerticalAlignment = -4108; % 垂直居中
%% 设置字体颜色
% 找到最小值的位置
minall = min(comparealg,[],2);
[minindexX,minindexY]=find(comparealg==minall);
minLocations = [minindexX,minindexY]; % 最小值位置矩阵
% 转换最小值位置到 Excel 单元格地址并设置为红色
for i = 1:size(minLocations, 1)
% 计算 Excel 单元格地址
rowIndex = minLocations(i, 1) + 2; % +2 是因为数据从 C3 开始
colIndex = minLocations(i, 2) + 2; % +2 是因为数据从第三列开始
cellAddress = sprintf('%s%d', char('A' + colIndex-1), rowIndex);
sheet.Range(cellAddress).Font.Color = 255; % 设置字体颜色为红色
sheet.Range(cellAddress).Font.Bold = true; % 设置字体为加粗
end
% 假设每个函数的数据占据 5 行
numRowsPerFunction = 5;
numFunctions = 4; % F1, F2, F3, F4
startCol = 'A'; % 数据开始的列
endCol = 'R'; % 数据结束的列
startRow = 3; % 数据开始的行
% 加粗每个函数数据行的底部边框
for i = 1:numFunctions
% 计算函数数据块的最后一行
lastRow = startRow + i * numRowsPerFunction - 1;
% 构建范围字符串
rangeStr = sprintf('%s%d:%s%d', startCol, lastRow, endCol, lastRow);
% 获取范围
range = sheet.Range(rangeStr);
% 设置底部边框样式为加粗
range.Borders.Item('xlEdgeBottom').LineStyle = 1; % Continuous line
range.Borders.Item('xlEdgeBottom').Weight = 4; % Thick weight
end
%% 存数据指定 Excel 范围
range = sheet.Range('C3:R22');
% 将数据一次性写入指定范围
range.Value = comparealg;
%% 保存工作簿 指定为绝对路径
workbook.Save();
%% 清理
workbook.Close();
excelApp.Quit();
excelApp.release;
3、收敛性分析
就是一个常规的迭代曲线图。文献中这么排版了,在此列出前四个函数。
%% 绘制迭代曲线
clear;clc;close all
addpath Algorithms\
addpath Algorithms\
cd Algorithms\
s = what;
algorithms = s.m;
cd D:\智能优化算法\WO\定量分析
SearchAgents_no = 30;
Max_iteration = 100;
figure('NumberTitle','off', ...
'Color','w', ...
'Name','迭代曲线对比图', ...
'Units','centimeters', ...
'Position',[4,15,40,7])
tiledlayout(1,4)
for j=1:4
fn = j;
Function_name=strcat('F',num2str(fn));
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
[Min_AEO,~, AEO_curve] = AEO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj );
[Min_ARO,~, ARO_curve] = ARO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj );
[Min_BOA,~, BOA_curve] =GWO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
[Min_BWOA,~, BWOA_curve]=BWOA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
[Min_CHIO,~, CHIO_curve]=CHIO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
[Min_FDA,~, FDA_curve]=FDA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
[Min_GA,~, GA_curve]=GA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
[Min_GWO,~, GWO_curve]=GWO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
[Min_MFO,~, MFO_curve]=MFO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
[Min_PSO,~, PSO_curve]=PSO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
[Min_SCSO,~, SCSO_curve]=SCSO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
[Min_SMA,~, SMA_curve]=SMA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
[Min_SOA,~, SOA_curve]=SOA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
[Min_SSA,~, SSA_curve]=SSA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
[Min_WO,~, WO_curve]=WO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
[Min_WOA,~, WOA_curve]=WOA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
nexttile
semilogy(AEO_curve)
hold on
semilogy(ARO_curve);semilogy(BOA_curve);semilogy(BWOA_curve);semilogy(CHIO_curve);
semilogy(FDA_curve);semilogy(GA_curve);semilogy(GWO_curve);semilogy(MFO_curve);
semilogy(PSO_curve);semilogy(SCSO_curve);semilogy(SMA_curve);semilogy(SOA_curve);
semilogy(SSA_curve);semilogy(WO_curve,'r','LineWidth',2);semilogy(WOA_curve);
xlabel('iteration')
ylabel('fitness')
end
% 填充算法名称 从加载的数据中读取
for i = 1:length(algorithms)
temp = strsplit(algorithms{i},'.');
algorithms(i)=temp(1);
end
legnedpos = gca().Position;
legend(algorithms,'Position',legnedpos+[legnedpos(3)+0.003,0,-0.1,0])

4、稳定性分析
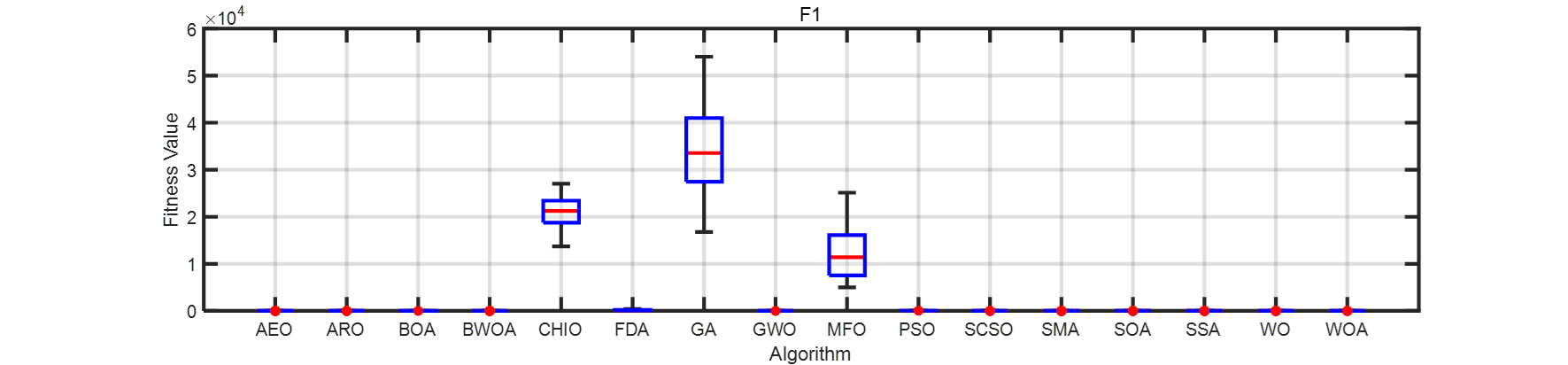
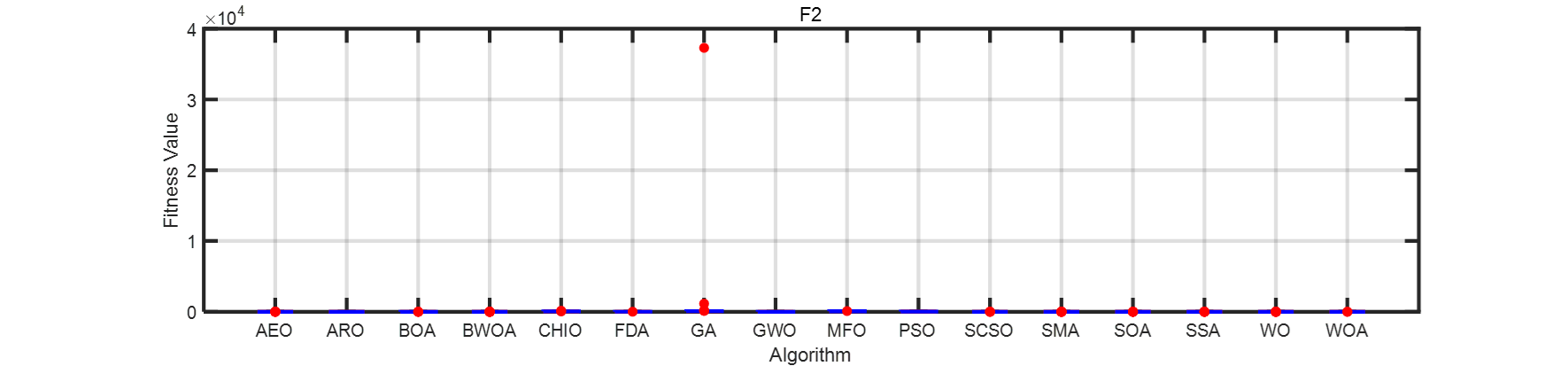
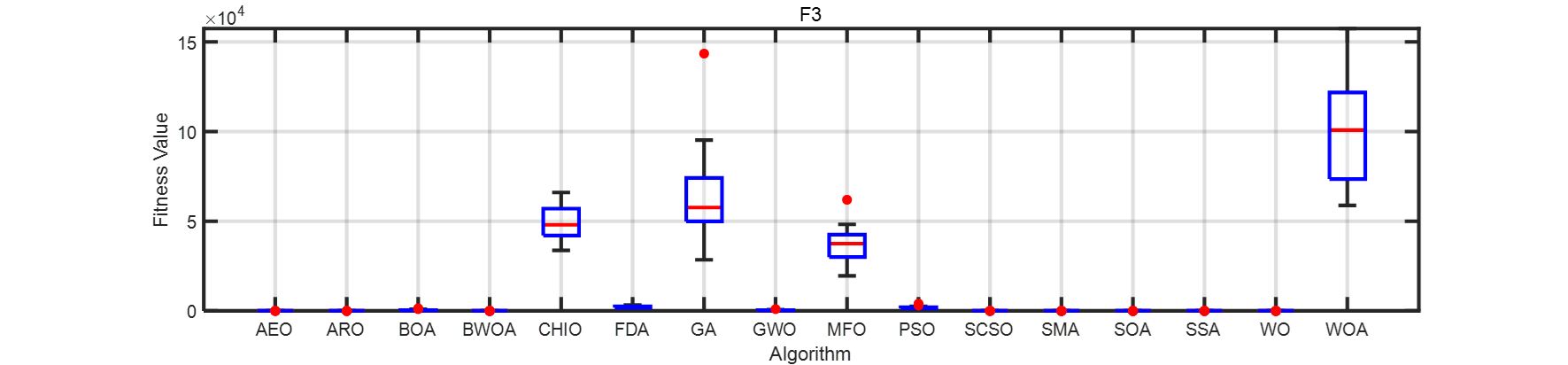
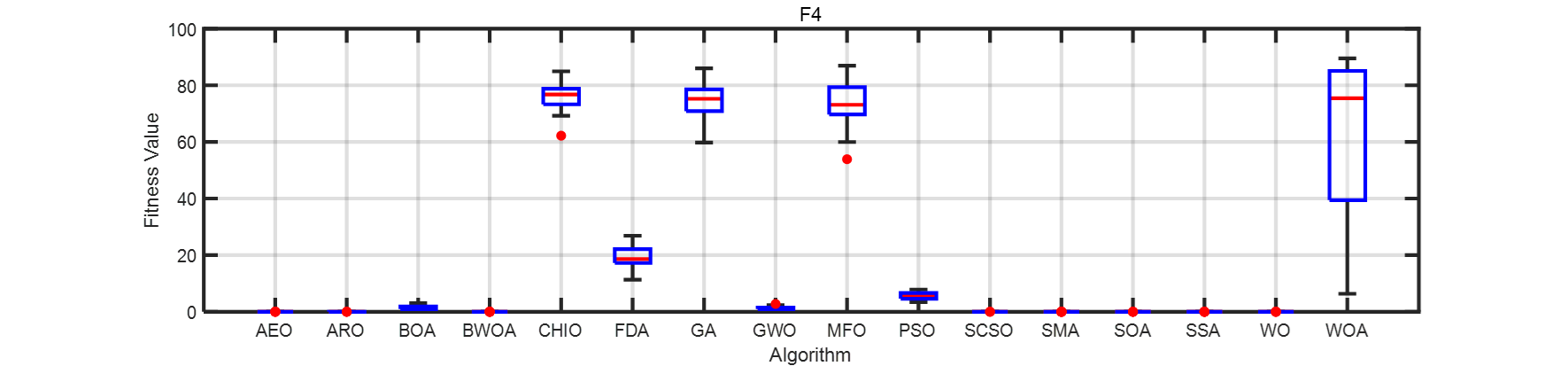
画了一个箱线图。在此列出matlab代码。
%% 稳定性分析
% 绘制箱线图
clc;clear;close all
% 加载独立运行得到的数据
load 20231107_30_100_30_16_PM.mat
% 填充算法名称 从加载的数据中读取
for i = 1:length(algorithms)
temp = strsplit(algorithms{i},'.');
algorithms(i)=temp(1);
end
% 绘制小提琴图
for i=1:4
F1 = resultall{i};
figure('NumberTitle','off', ...
'Color','w', ...
'Name','稳定性分析', ...
'Units','centimeters', ...
'Position',[4,15,30,7])
handelbox = boxchart(F1);
box on
set(gca,'xticklabels',algorithms, ...
'LineWidth',2)
xlabel('Algorithm')
ylabel('Fitness Value')
grid on
handelbox.BoxFaceColor = 'w';
handelbox.BoxEdgeColor = 'b';
handelbox.BoxMedianLineColor = 'r';
handelbox.LineWidth = 2;
handelbox.MarkerColor = 'r';
handelbox.MarkerStyle = ".";
handelbox.MarkerSize = 15;
title(strcat('F',num2str(i)))
end
5、灵敏性分析
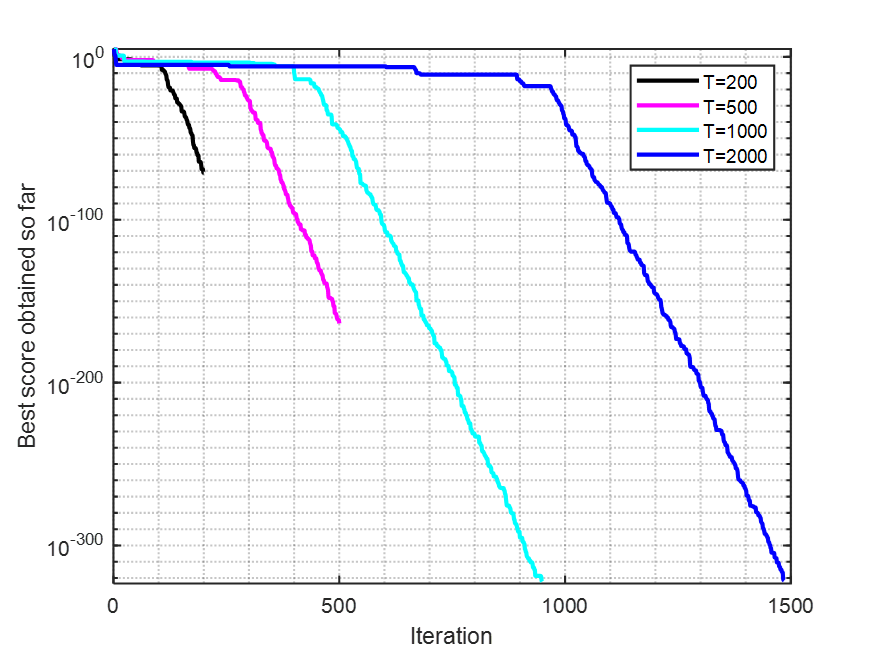
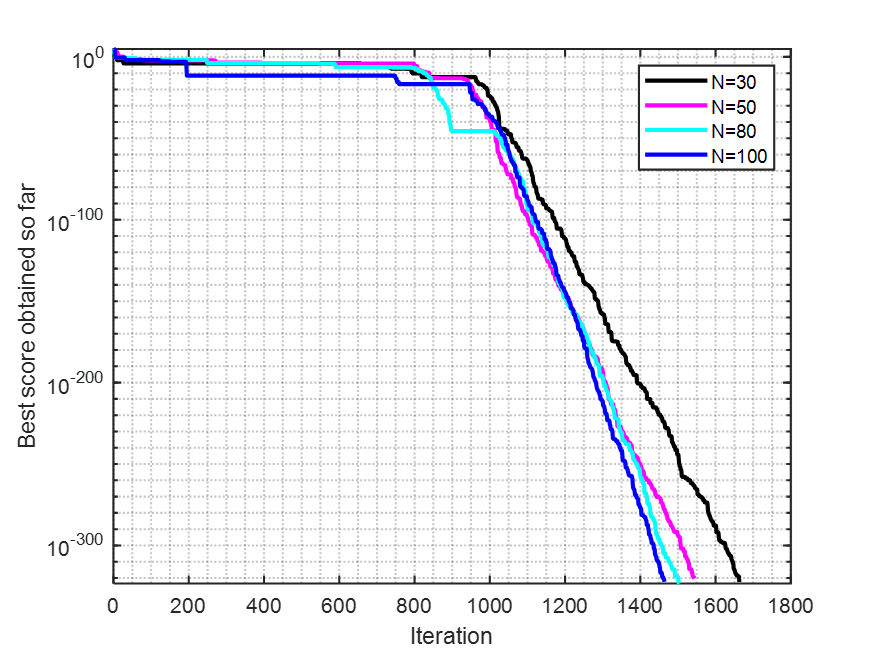
这个分析就是来寻找算法的最佳参数设置。文中选取了最大迭代次数,种群个数以及雄性个体占比三个参数。
原文中,图7 ( a )和( b )分别展示了F1在不同的最大迭代次数和搜索代理数下的WO收敛曲线。图7 ( c )展示了WO在F5上的收敛曲线,以及不同比例的雄性个体在群体中的分布。计算结果和可视化表明,当最大迭代次数增加时,WO收敛到最优解。此外,从图7 ( b )可以看出,当种群数量的数量增加时,迭代次数减少。图7 ( c )显示了当p从0.3到0.4时WO的相对稳定的行为。基于此分析,p的最佳值可以被建议为其最大值(即p = 0.45),其中WO的结果最好。
clear ;clc;close all
%% F5 6 12 13 14 15
populationSize = [30,50,80,100];
Max_iteration = [200,500,1000,2000];
p = [0.3,0.35,0.4,0.45];
populationSize=populationSize(4);
p = p(4);
fn=1;
Function_name=strcat('F',num2str(fn));
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
colormap = ['k','m','c','b'];
figure('Color','w')
for i=1:length(Max_iteration)
rng('shuffle');
[Best_score,Best_pos,WO_cg_curve]=WO(populationSize,Max_iteration(i),lb,ub,dim,fobj,p);
semilogy(WO_cg_curve,colormap(i),'LineWidth',2)
hold on
end
set(gca,'XMinorGrid','on','YMinorGrid','on', ...
'LineWidth',1)
legend({'T=200';'T=500';'T=1000';'T=2000'})
xlabel('Iteration')
ylabel('Best score obtained so far')
clear ;clc;close all
%% F5 6 12 13 14 15
populationSize = [30,50,80,100];
Max_iteration = [200,500,1000,2000];
p = [0.3,0.35,0.4,0.45];
Max_iteration =Max_iteration(4);
p = p(4);
fn=1;
Function_name=strcat('F',num2str(fn));
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
colormap = ['k','m','c','b'];
figure('Color','w')
for i=1:length(populationSize)
rng('shuffle');
[Best_score,Best_pos,WO_cg_curve]=WO(populationSize(i),Max_iteration,lb,ub,dim,fobj,p);
semilogy(WO_cg_curve,colormap(i),'LineWidth',2)
hold on
end
set(gca,'XMinorGrid','on','YMinorGrid','on', ...
'LineWidth',1)
% legend({'T=200';'T=500';'T=1000';'T=2000'})
legend({'N=30';'N=50';'N=80';'N=100'})
% legend({'T=200';'T=500';'T=1000';'T=2000'})
xlabel('Iteration')
ylabel('Best score obtained so far')
clear ;clc;close all
%% F5 6 12 13 14 15
populationSize = [30,50,80,100];
Max_iteration = [200,500,1000,2000];
p = [0.3,0.35,0.4,0.45];
populationSize=populationSize(4);
Max_iteration =Max_iteration(4);
fn=5;
Function_name=strcat('F',num2str(fn));
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
colormap = ['k','m','c','b'];
figure('Color','w')
for i=1:length(p)
rng('shuffle');
[Best_score,Best_pos,WO_cg_curve]=WO(populationSize,Max_iteration,lb,ub,dim,fobj,p(i));
semilogy(WO_cg_curve,colormap(i),'LineWidth',2)
hold on
end
set(gca,'XMinorGrid','on','YMinorGrid','on', ...
'LineWidth',1)
% legend({'T=200';'T=500';'T=1000';'T=2000'})
% legend({'N=30';'N=50';'N=80';'N=100'})
legend({'P=0.30';'P=0.35';'P=0.40';'P=0.45'})
xlabel('Iteration')
ylabel('Best score obtained so far')
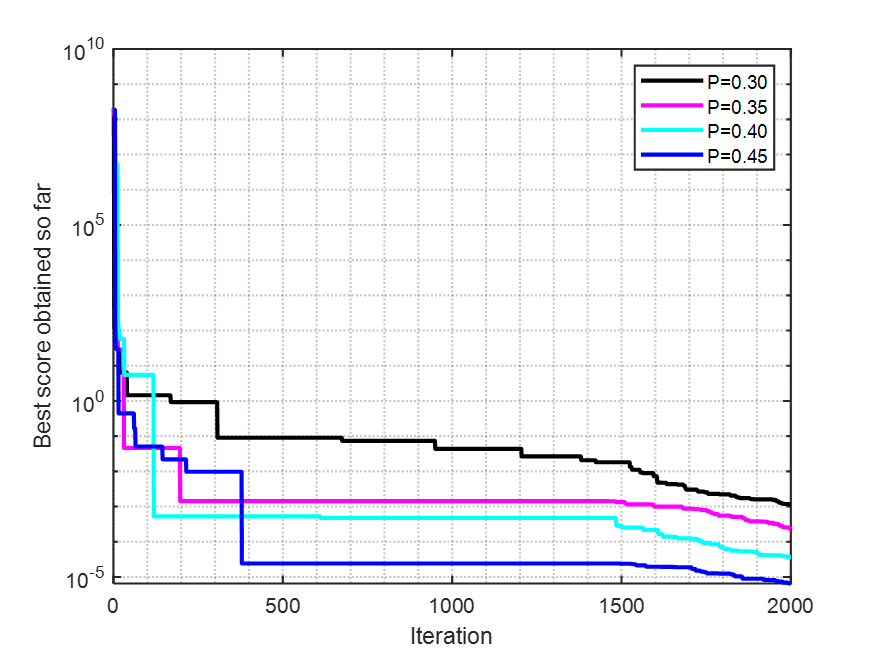
从上面三幅图中可以看出,T,N,P三个参数都有影响。种群个数和迭代次数的增加会导致算法时间上的增加,在做具体案例分析时,应该选择合适的迭代次数和种群个数;P值的影响不会特别大,按照原文献的介绍,我也用F5测试函数,想要达到文献的效果。是需要多次运行的,这些P值在解决具体问题的时候,个人觉得不会影响特别大。P在[0.30,0.45]之间都可以。源代码上P值默认设置的是0.4。
6、可扩充性分析
通过改变F1 ~ F13的维度来测试所提出的WO的可扩展性,以确定增加维度对不同测试函数计算结果的影响。测试函数的维度分别为50、100、500。文献中对其进行了大量分析,用了13个测试函数,做了三个表格,感兴趣的可以参考一下。最后对所有算法进行Friedman检验,做了一个排名,证明了所提算法的优越性。
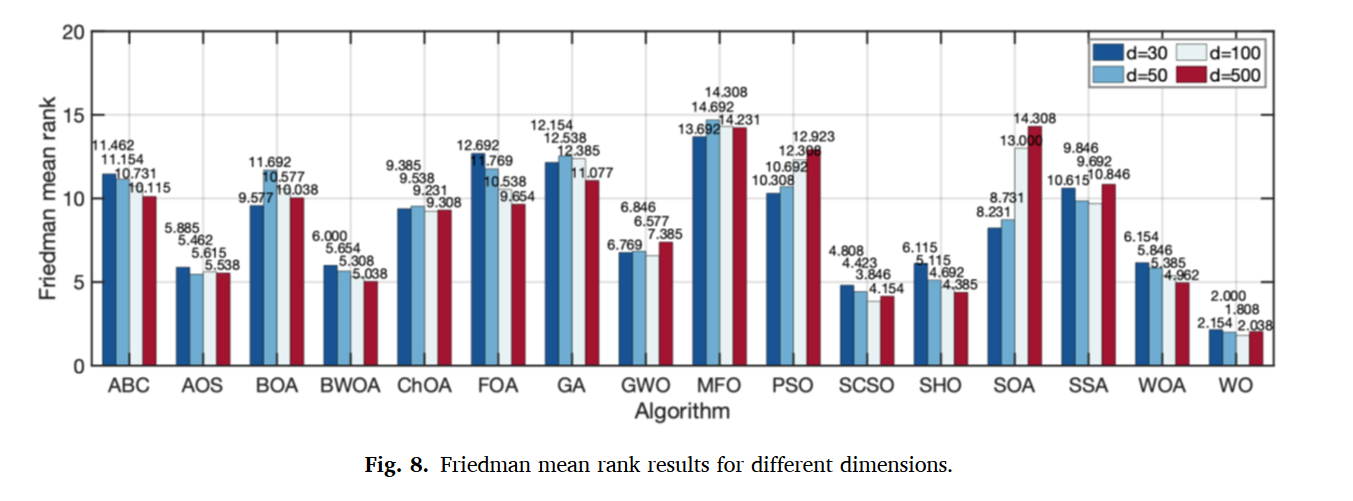
结果表明,WO排在第一位,而SCSO、SHO和WOA分别排在第二位、第三位和第四位。
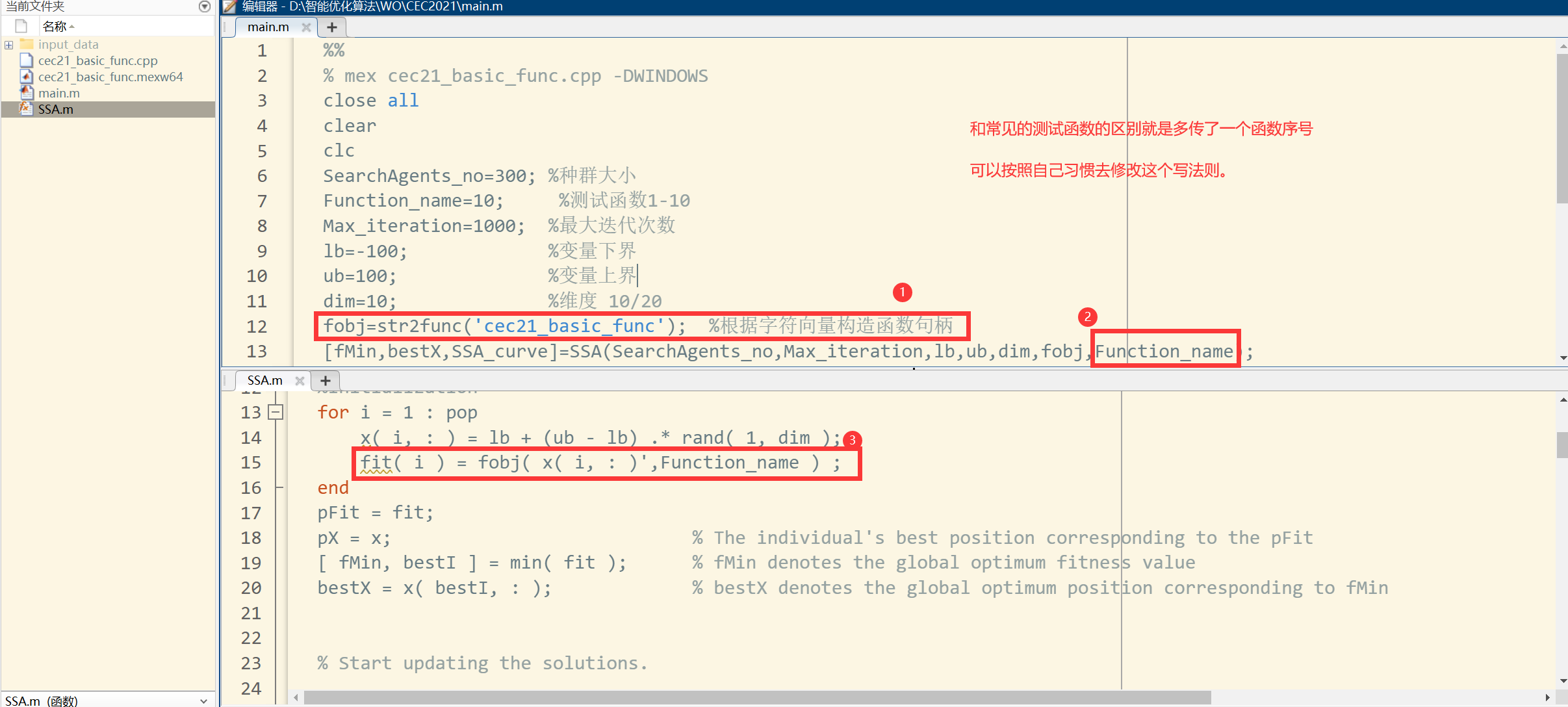
CEC2021测试函数
测试函数下载地址
这节中,作者又换了几个算法。做了定量分析,收敛性分析和稳定性分析。我不再重复绘图了。在这简单说一下CEC系列的函数怎么使用吧。CEC系列的测试函数有很多,一般下载下来就会给你编译好的matlab可执行文件,后缀名.mexw64。以CEC2017为例
1. run the following command in Matlab window:
mex cec17_func.cpp -DWINDOWS
2. Then you can use the test functions as the following example:
f = cec17_func(x,func_num);
here x is a D*pop_size matrix.
实际工程优化问题
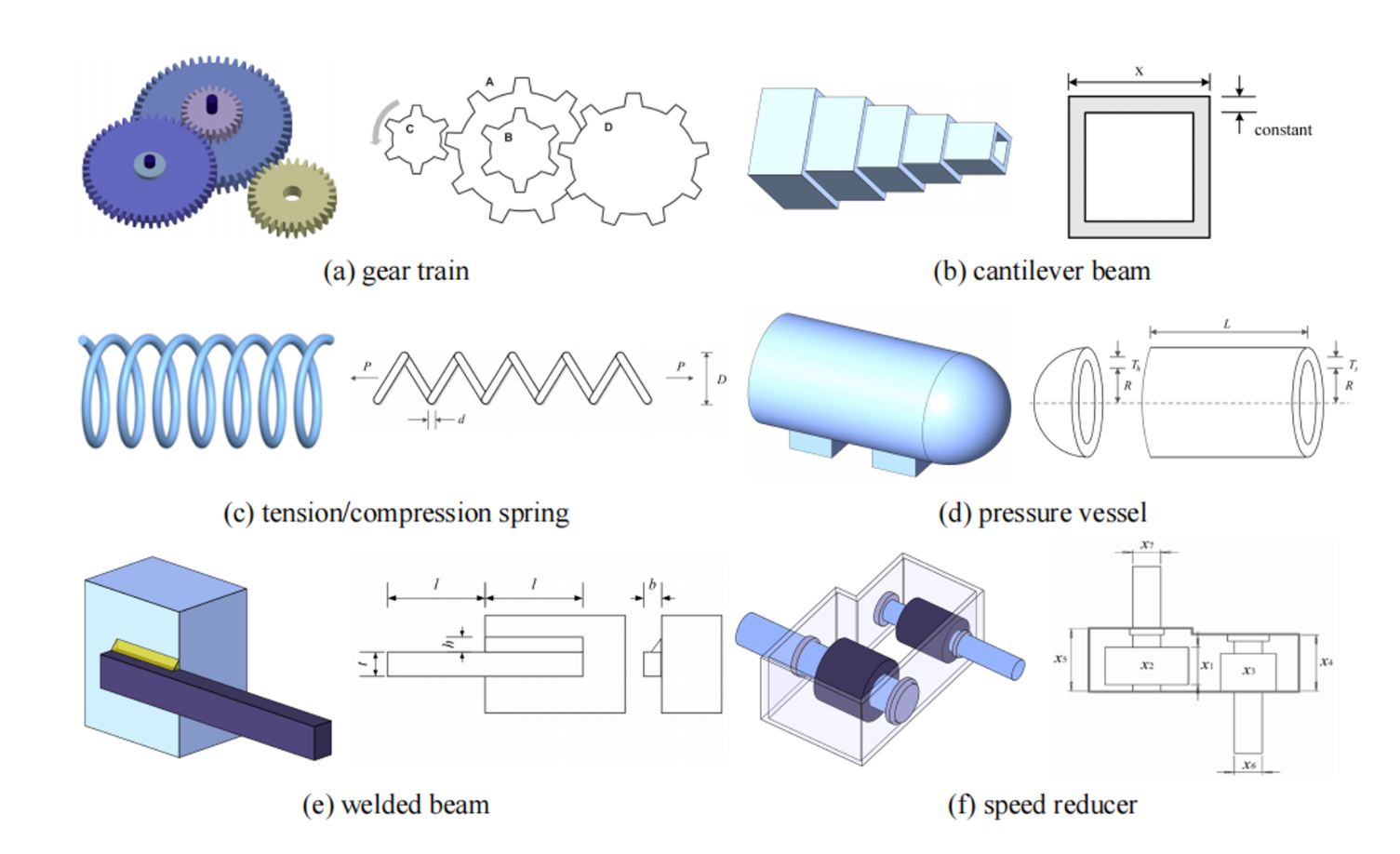

经典工程优化malab代码下载链接

注:原文已经进行大量实验结果分析,感兴趣的请阅读原文,学习学习一篇好的论文是怎么写的。源代码也已公开,我就不点运行和截图了,大家自行下载。
特别提示:不要买什么基本的算法,这些算法都是全网公开的,优秀的东西从来都不保密,不怕任何人抄袭的,各位不要再交智商税了。
