机器学习第7天:逻辑回归
文章目录
介绍
概率计算
逻辑回归的损失函数
单个实例的成本函数
整个训练集的成本函数
鸢尾花数据集上的逻辑回归
Softmax回归
Softmax回归数学公式
Softmax回归损失函数
调用代码
参数说明
结语
介绍
作用:使用回归算法进行分类任务
思想:将回归值转为概率值,然后找到一个适当的数值,当概率大于这个值时,归为一类,当小于这个值时,归为另一类
概率计算
函数的输入值为特征的加权和
是sigmoid函数,公式为
函数图像为

可见它输出一个0-1的值,我们可以将这个值当作概率
则我们可以通过这个概率来分类,设定一个值,在这个值的两端进行分类
逻辑回归的损失函数
单个实例的成本函数
当p>=0.5时
当p<0.5时
整个训练集的成本函数
这个损失函数也是一个凸函数,可以使用梯度下降法使损失最小化
鸢尾花数据集上的逻辑回归
鸢尾花数据集是机器学习中一个经典的数据集,它有花瓣和花萼的长和宽,任务是用它们来判断鸢尾花的种类
看代码和效果
from sklearn import datasets
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt
import numpy as np
iris = datasets.load_iris()
x = iris["data"][:, 3:]
y = (iris["target"] == 2)
model = LogisticRegression()
model.fit(x, y)
x_new = np.linspace(0, 3, 1000).reshape(-1, 1)
y_proba = model.predict_proba(x_new)
plt.plot(x_new, y_proba[:, 1], "g-", label="Iris virginica")
plt.plot(x_new, y_proba[:, 0], "b--", label="Not Iris virginica")
plt.xlabel("Petal width")
plt.ylabel("probability")
plt.legend()
plt.show()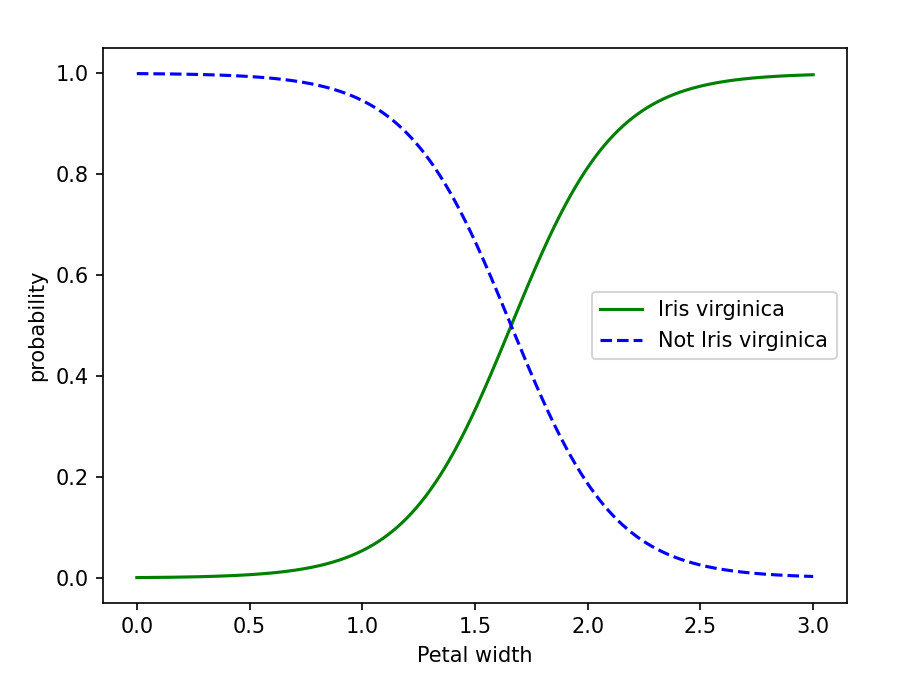
可以看见,当花瓣长度变化的时候,两种花种类的概率随之变化
简单介绍一下新的代码,predict.proba方法返回样本为可能的两种花的概率。
Softmax回归
上述方法主要用于二分类任务,我们再来看一种多分类方法,Softmax回归
Softmax回归数学公式
Softmax函数也叫指数归一化函数,它对x进行指数处理再进行归一化得出一个概率
这个函数的自变量为一个分数s,这个s由我们的数据的转置矩阵与一个参数相乘得来
对于不同的类,参数都不相同,模型训练的任务就是拟合这个参数
Softmax回归损失函数
当k=2时(二分类),此成本函数等于sigmoid逻辑回归的成本函数
调用代码
model = LogisticRegression(multi_class="multinomial", solver="lbfgs", C=10)
model.fit(x, y)参数说明
multi_class="multinomial": 表示采用多类别分类,即多类别的逻辑回归问题,与二元逻辑回归不同。
solver="lbfgs": 表示使用LBFGS(Limited-memory Broyden–Fletcher–Goldfarb–Shanno)优化算法进行求解。
C=10: 表示正则化参数,控制模型的正则化强度,C值越小,正则化强度越高。
结语
逻辑回归是一种简单的分类方法,二分类任务就用第一种方法,多分类任务就用第二种方法
