动态规划背包问题总结

背包问题分类繁多,对刚学习动态规划的新手的来说难度不小,接下来就来仔细理一理背包问题

首先我们先不管背包问题有几种分类,反正讲了也不会有什么深刻的认识,只有你真正做题遇到了,你来能感受到他大概是怎么样的

回到最初的起点,我们需要搞明白的是:

什么是背包问题?

我们可以问问gpt,gpt给出这样的解释:

背包问题的描述是：给定一系列物品的重量和价值，以及一个背包的容量，如何选择物品，使得装入背包的物品总价值最大，且背包内物品总重量不能超过背包容量。

更具体来说：

• 给定n个物品，每个物品i有一个重量w和一个价值v
• 给定一个背包的容量S
• 目标是选择某些物品，使得这些物品的总重量不超过S,且这些物品的总价值最大

解决这个问题需要考虑每个物品是否选择的所有可能组合，然后计算每个组合的总价值。由于组合数目太多，直接枚举是不可行的。背包问题适合使用动态规划的思想，从子问题向上构建问题的最优解。

简单说就是你有一个容量为size的背包,然后有一堆物品,每个物品的重量(体积)weight,和价值value不同(也有相同的情况),你需要用你的背包去解决一系列问题,例如怎样装背包内物品价值最高?装满背包有几种方法?...

这些问题可谓五花八门,为了搞懂背包问题,我会按照分类和题目对背包问题进行一次总结

问题分类

对背包问题有了初步了解之后,我们就可以大概认识一下背包问题有多少种类了

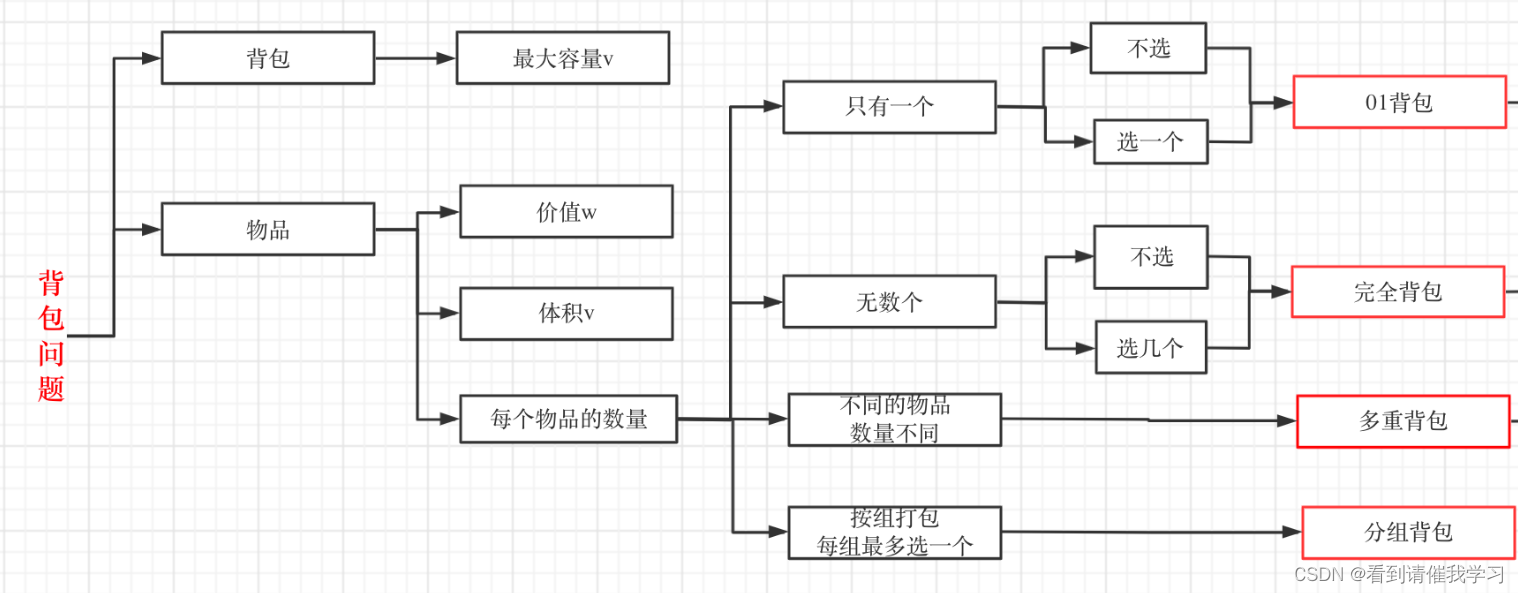
这里借用一下卡哥的图,主要是按照物品的数量进行分类的

01背包:一个物品只有一个,也就是说一个物品只能选取一次,这样就不用考虑重复选取的问题了,为什么叫01背包呢,因为物品只有两种状态:0(不放入),1(放入)

完全背包:

多重背包:

分组背包:

背包问题怎么写?

我们通过最简单的01背包问题来学习一下背包问题的算法

题目如下: 

我们之前已经学习过动规五部曲了(也可以简化为三步,确定dp数组,初始化dp数组,dp递推公式),但是在做的时候总感觉下不了手(我自己做的时候就有这种感觉,题目变难了难以下手)

这里拆分成三步去设计算法

第一步确定dp数组:

我们知道dp数组就是表示状态的,这里我们要求的状态就是:从0到i个物品中任意取放入容量为j的背包中的最大价值总和

我们往往使用行来表示即将要放入的物品,用列来表示背包的容量

那么我们就可以确定dp数组为dp[i][j],其中i为即将放入的物品,它有两种状态放或不放;j表示背包的容量

 

第二步初始化dp数组: