时间序列预测 — LSTM实现多变量多步负荷预测(Keras)
目录
1 数据处理
1.1 数据集简介
1.2 数据集处理
2 模型训练与预测
2.1 模型训练
2.2 模型多步预测
2.3 结果可视化
1 数据处理
1.1 数据集简介
实验数据集采用数据集6:澳大利亚电力负荷与价格预测数据(下载链接),包括数据集包括日期、小时、干球温度、露点温度、湿球温度、湿度、电价、电力负荷特征,时间间隔30min。

单独查看部分负荷数据,发现有较强的规律性。

1.2 数据集处理
首先检查数据的缺失值情况,通过统计数据可以看到,数据比较完整,不存在缺失值。其他异常值和数据处理可以自行处理。
# 缺失值统计
data.isnull().sum()计划预测后一天的数据48个,将要预测的数据保留(也就是未来未知的数据),单独提取出前面训练的数据(也就是历史数据),并对数据集进行滚动划分。跟前面文章的划分方式不同,因为是多变量,特征和标签分开划分,不然后面处理会有很多问题。

# 训练数据,也就是历史数据
dataf = data.values[0:-48]#构造数据集
def create_dataset(datasetx,datasety,timesteps=36,predict_size=6):
datax=[]#构造x
datay=[]#构造y
for each in range(len(datasetx)-timesteps - predict_steps):
x = datasetx[each:each+timesteps,0:6]
y = datasety[each+timesteps:each+timesteps+predict_steps,0]
datax.append(x)
datay.append(y)
return datax, datay#np.array(datax),np.array(datay)接着设置预测的时间步、每次预测的步长、最后总的预测步长,参数可以根据需要更改。跟前面文章不同的是,这里没有滚动预测,因为没有持续的特征传入,在实际运用有特征传入时可以滚动预测。
#构造train and predict
train = dataf.copy()
timesteps = 48 #构造x,为48个数据,表示每次用前48个数据作为一段
predict_steps = 48 #构造y,为48个数据,表示用后12个数据作为一段
length = 48 #预测多步,预测48个数据,每次预测48个接着对数据进行归一化处理,跟前面文章的处理方式不同,特征和标签分开划分,并分开进行归一化处理。
# 特征和标签分开划分
datafx = dataf[:,0:5]
datafy = dataf[:,5].reshape(25872,1)
# 分开进行归一化处理
scaler1 = MinMaxScaler(feature_range=(0,1))
scaler2 = MinMaxScaler(feature_range=(0,1))
datafx = scaler1.fit_transform(datafx)
datafy = scaler2.fit_transform(datafy)最后对这行数据集进行划分,并将数据变换为满足模型格式要求的数据。
trainx, trainy = create_dataset(datafx,datafy,timesteps, predict_steps)
trainx = np.array(trainx)
trainy = np.array(trainy)2 模型训练与预测
2.1 模型训练
首先搭建模型的常规操作,然后使用训练数据trainx和trainy进行训练,进行20个epochs的训练,每个batch包含200个样本。此时input_shape划分数据集时每个x的形状。
#lstm training
model = Sequential()
model.add(LSTM(128,input_shape=(timesteps,5),return_sequences= True))
model.add(Dropout(0.5))
model.add(LSTM(128,return_sequences=True))
#model.add(Dropout(0.3))
model.add(LSTM(64,return_sequences=False))
#model.add(Dropout(0.2))
model.add(Dense(predict_steps))
model.compile(loss="mean_squared_error",optimizer="adam")
model.fit(trainx,trainy, epochs= 20, batch_size=200)2.2 模型多步预测
下面介绍文章中最重要,也是真正没有未来特征的情况下预测未来标签的方法。整体的思路也就是,前面通过前48个数据训练后面的48个未来数据,预测时取出前48个数据预测未来的48个未来数据。这里与单变量预测不同,没有进行滚动预测,因为单变量预测的结果可以作为历史数据进行滚动,这里多变量只产生了预测值,并没有预测标签,不能进行滚动预测,在实际有数据源源不断时可以采用滚动预测。(里面的数据可以根据需求进行更改)

首先提取需要带入模型的数据,也就是预测前的timesteps行特征。
predict_xlist = []
predict_xlist.extend(dataf[dataf.shape[0]-timesteps:dataf.shape[0],0:5].tolist())
predictx = np.array(predict_xlist[-timesteps:])
predictx = np.reshape(predictx,(1,timesteps,5))#变换格式,适应LSTM模型准备好数据后,接着进行预测,并对预测结果进行反归一化。
# 预测
lstm_predict = model.predict(predictx)
# 反归一化
lstm_predict = scaler2.inverse_transform(lstm_predict)
# 提取预测值,方便对比
predict_y = []
predict_y.extend(lstm_predict[0])2.3 结果可视化
计算误差,并保存预测结果,并进行可视化。
#error
y_ture = np.array(data.values[-48:,5])
train_score = np.sqrt(mean_squared_error(y_ture,predict_y))
print("train score RMSE: %.2f"% train_score)
y_predict = pd.DataFrame(predict_y,columns=["predict"])
y_predict.to_csv("y_predict_LSTM.csv",index=False)# 可视化
from itertools import cycle
cycol = cycle('bgrcmk')
plt.figure(dpi=100,figsize=(14,5))
plt.plot(y_ture,c=next(cycol),markevery=5)
plt.plot(y_predict,c=next(cycol),markevery=5)
plt.legend(['y_ture','y_predict'])
# 坐标描述
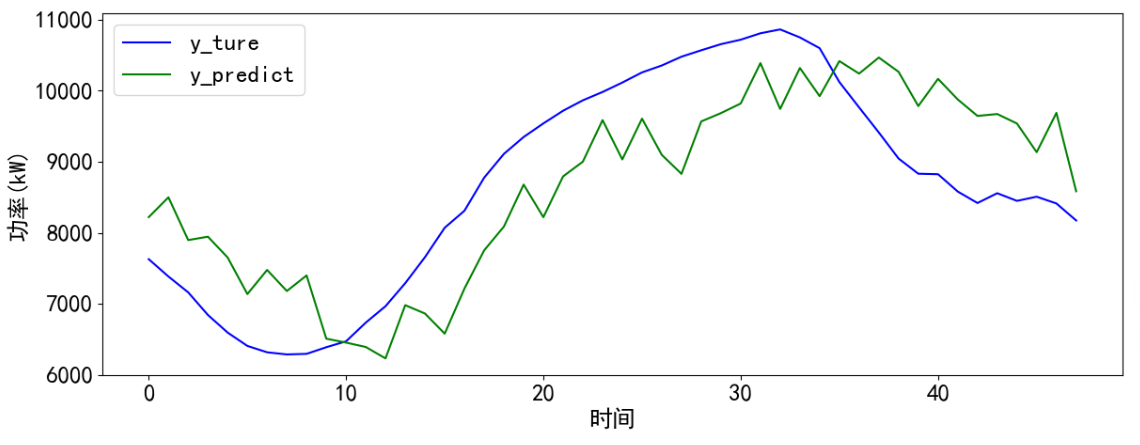
plt.xlabel('时间')
plt.ylabel('功率(kW)')
plt.show() 最后可视化运行结果,发现预测的效果大致捕捉了趋势,预测值存在一定程度的波动。