每日一题--寻找重复数
蝶恋花-王国维
阅尽天涯离别苦,
不道归来,零落花如许。
花底相看无一语,绿窗春与天俱莫。
待把相思灯下诉,一缕新欢,旧恨千千缕。
最是人间留不住,朱颜辞镜花辞树。

目录
题目描述:
思路分析:
方法及时间复杂度:
法一 排序数组(暴力解法):
法二 哈希表
法三 二分查找(经典解法)
法四 快慢指针
法五 二进制(烧脑解法)
个人总结:
题目描述:

287. 寻找重复数 - 力扣(LeetCode)
思路分析:
在一个数组中查找唯一重复的元素,可以用很多解法,立马想到的便是哈希表。将数组元素插入哈希表,然后查找哈希表,找到了就返回该数
方法及时间复杂度:
法一 排序数组(暴力解法):
将数组进行排序,这样重复的元素一定相邻,然后遍历排序后的数组就行。代码如下:

int cmp(const void*a,const void*b){
return *(int*)a-*(int*)b;
}
int findDuplicate(int* nums, int numsSize) {
qsort(nums,numsSize,sizeof(int),cmp);
for(int i=1;i<numsSize;++i){
if(nums[i]==nums[i-1]){
return nums[i];
}
}
return -1;
}时间复杂度O(nlogn) 排序的时间nlogn
空间复杂度O(1)
法二 哈希表
利用哈希表查找哈希表中存在的元素,即数组重复的元素。可以使用c++容器的哈希集合unordered_set,这里用c语言数组模拟了一个哈希表。代码如下:
int findDuplicate(int* nums, int numsSize) {
int hash[100001]={0};//初始化哈希表所有元素为0
for(int i=0;i<numsSize;++i){
if(hash[nums[i]]){//查找哈希表中是否存在该元素
return nums[i];
}
hash[nums[i]]++;
}
return -1;
}时间复杂度O(n)
空间复杂度O(n) 空间换时间了属于是
法三 二分查找(经典解法)
用此方法前先弄清楚什么是鸽巢原理。
鸽巢原理:也称为抽屉原理,是一个基本的数学原理,这个原理的经典解释是,就像将若干只鸽子放在若干个鸽巢中一样,如果鸽子的数量大于鸽巢的数量,那么至少有一个鸽巢中放了两只鸽子。

这里抽象成二分查找那个装有两只鸽子的鸽巢
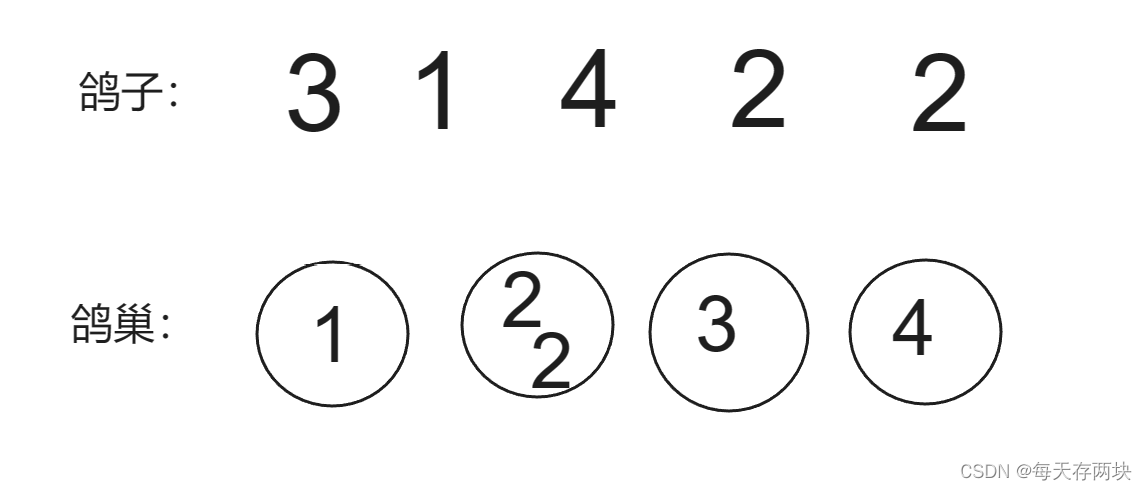
二分查找的区间很明显就是【1,n-1】,n为数组长度。查找中点mid(先猜一个鸽巢),遍历数组并记录<=mid的数,如果<=mid的数大于mid说明这个有着两只鸽子的鸽巢在左区间,反之,如果<=mid的数小于等于mid,就在右区间。直到left==right时,这个鸽巢就是有着两只鸽子的鸽巢。
代码如下:
int findDuplicate(int* nums, int numsSize) {
int left=1,right=numsSize-1;
while(left<right){
int mid=(left+right)>>1;
int cnt=0;
for(int i=0;i<numsSize;++i){
if(nums[i]<=mid){
cnt++;
}
}
if(cnt>mid){
right=mid;
}else{
left=mid+1;
}
}
return left;
}时间复杂度O(nlogn) 二分查找时间复杂度 logn,然后每次查找都要遍历数组O(n)
空间复杂度O(1)
法四 快慢指针
下标向值引一条边,值向下标引一条边,从0开始沿着箭头走,逐渐就会进入一个环,环的入口就是重复的元素。
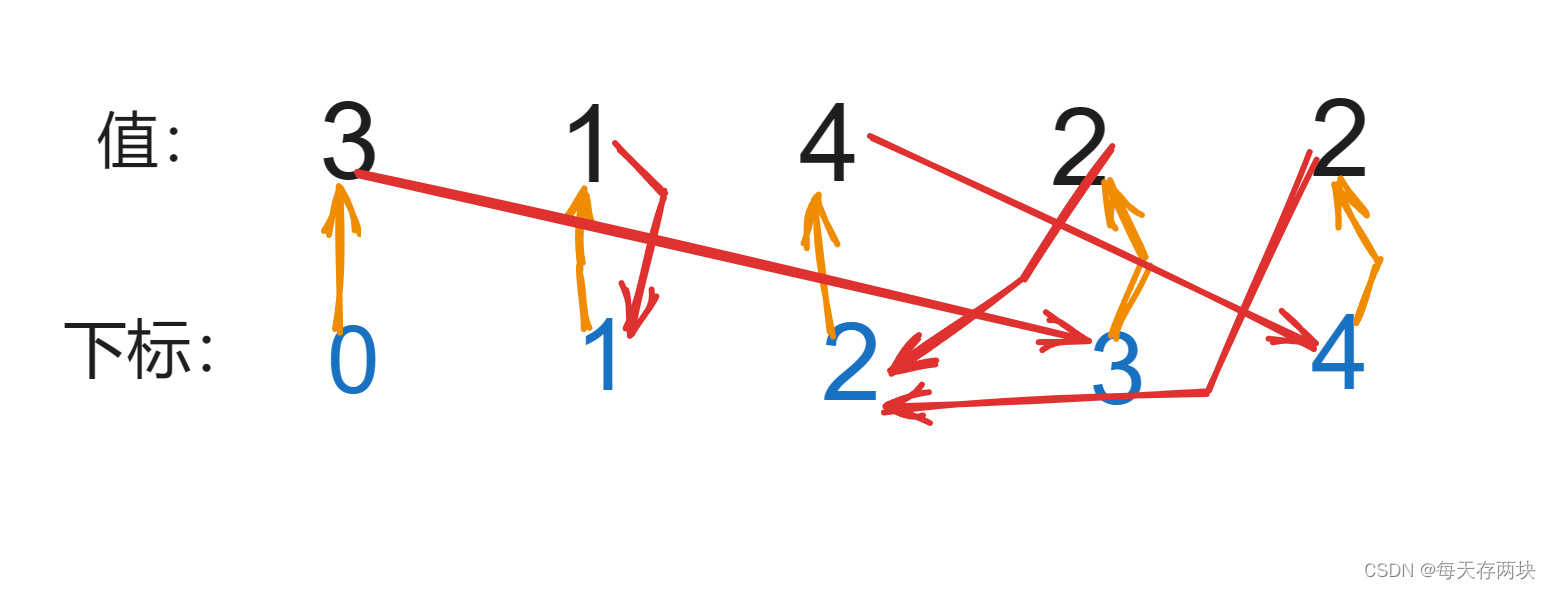
类似于环形链表,定义快指针fast,慢指针slow。慢指针每次走一步,快指针每次走两步,快指针会在环里追上慢指针,然后让快指针从0开始走,快慢指针同时走一步,相逢时就是环的入口,即重复元素。
代码如下:
int findDuplicate(int* nums, int numsSize) {
int slow=0,fast=0;
do{
slow=nums[slow];
fast=nums[nums[fast]];
}while(slow!=fast);
fast=0;
while(slow!=fast){
slow=nums[slow];
fast=nums[fast];
}
return slow;
}时间复杂度O(n)
空间复杂度O(1)
法五 二进制(烧脑解法)
可以使用二进制位运算来解决此题。我们可以将数组 nums 中的每一个数字用二进制来表示,最多只需要 log(n) 位,其中 n 是数组 nums 的长度。
对于每一位 i,我们可以计算在此位上所有数字出现的次数之和。如果某一位上的出现次数之和大于 2,说明出现了重复的数字。
具体做法如下:
- 对于二进制的第 i 位,计算所有数字的二进制表示中第 i 位上出现 1 的次数之和(可以使用位运算和移位操作进行统计)。
- 如果第 i 位上出现 1 的次数之和大于 2,说明重复数字在此位上的值为 1,否则为 0。
- 将所有位上确定的二进制位还原成对应的十进制数字,即为重复的数字。
代码如下:
int findDuplicate(int* nums, int n) {
int ans = 0;
// 确定二进制下最高位是多少
int bit_max = 31;
while (!((n - 1) >> bit_max)) {
bit_max -= 1;
}
for (int bit = 0; bit <= bit_max; ++bit) {
int x = 0, y = 0;
for (int i = 0; i < n; ++i) {
if (nums[i] & (1 << bit)) {
x += 1;
}
if (i >= 1 && (i & (1 << bit))) {
y += 1;
}
}
if (x > y) {
ans |= 1 << bit;
}
}
return ans;
}时间复杂度O(nlogn) 枚举二进制数的位数个数O(logn)
空间复杂度O(1)
个人总结:
二分查找的算法其实还可以优化。 有位大师曾经说过,完成比完美更重要。
