B树与B+树的对比
B树:
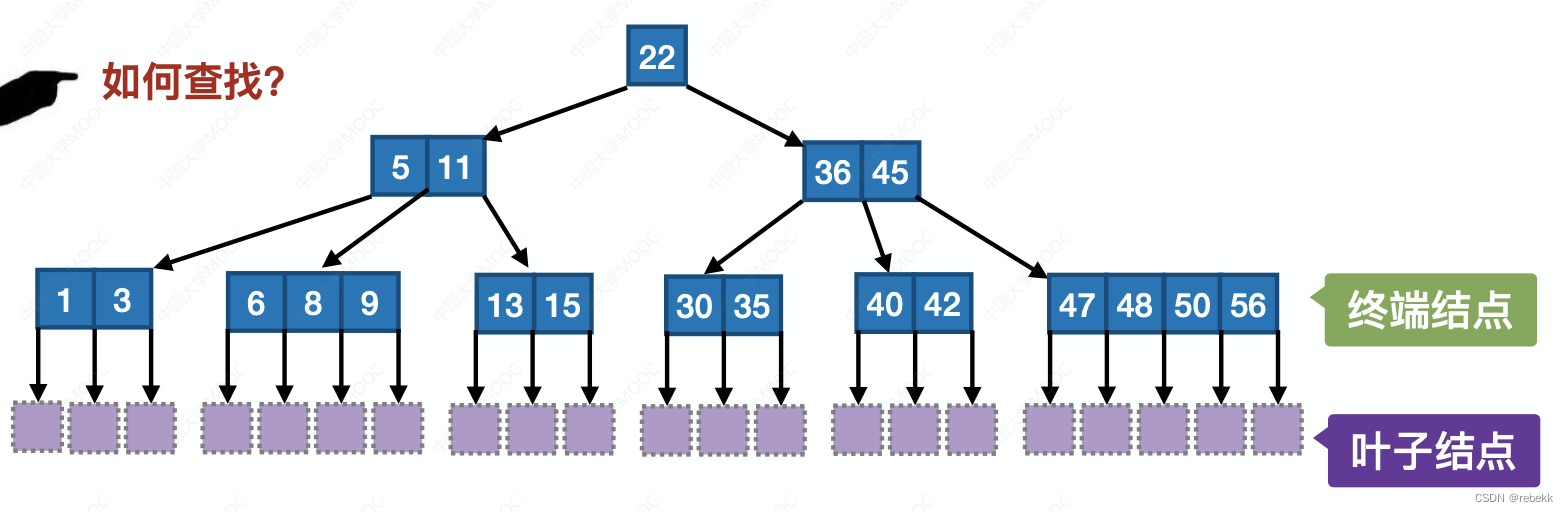
m阶B树的核心特性:
- 树中每个节点至多有m棵子树,即至多含有m-1个关键字
- 根节点的子树数属于[2, m],关键字数属于[1, m-1],其他节点的子树数属于 [ ⌈ m 2 ⌉ , m ] [\lceil \frac{m}{2}\rceil, m] [⌈2m⌉,m],关键字数属于 [ ⌈ m 2 ⌉ − 1 , m − 1 ] [\lceil \frac{m}{2}\rceil-1, m-1] [⌈2m⌉−1,m−1]
- 对任一节点,其所有子树高度都相同
- 关键字的值:子树0<关键字1<子树1<关键字2<…(类比二叉查找树 左<根<右)
- 所有叶节点都出现在同一层次上,且不带信息(可以视为外部节点或类似于折半查找判定树的查找失败节点,实际上这些节点不存在,指向这些节点的指针为空)
B+树
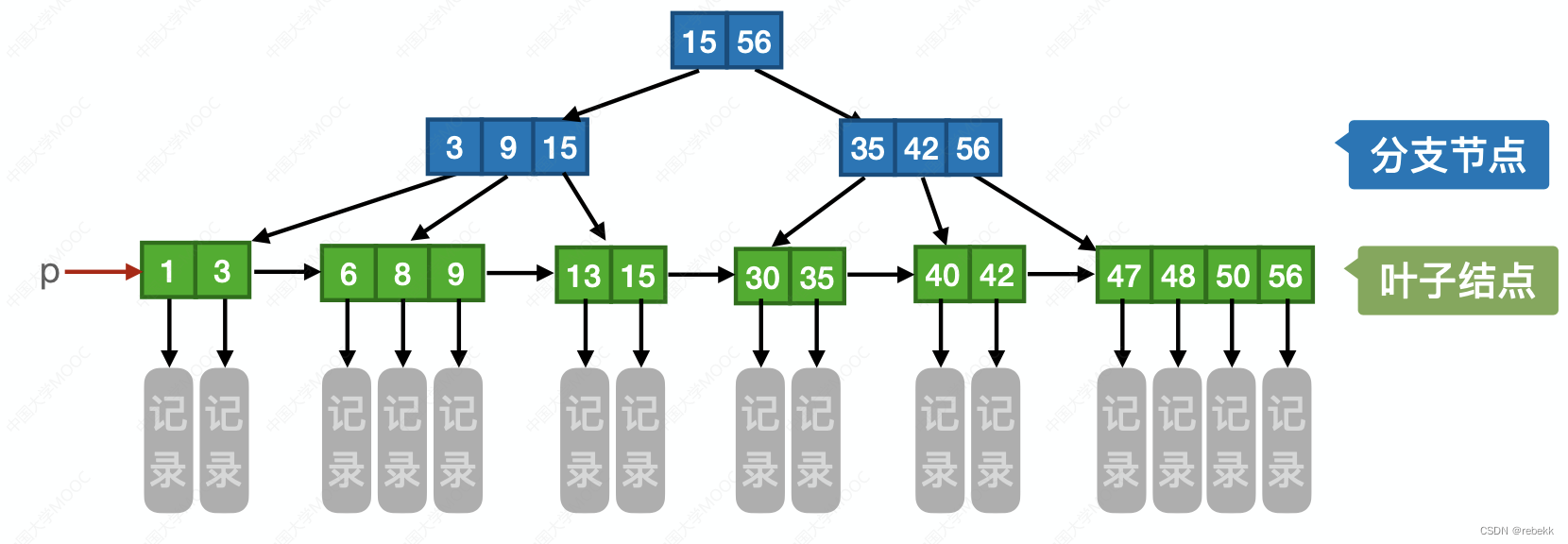
m阶B+树的核心特性:
- 通常在B+树上有两个头指针,一个指向根节点,另一个指向关键字最小的叶子节点。因此可对B+树进行两种查找运算,一种是从最小关键字起顺序查找,另一种是从根节点开始,进行随机查找
- 树中每个节点至多有m棵子树;(节点的子树个数与关键字个数相等)
- 根节点的子树数属于[2, m],其他节点的子树数属于 [ ⌈ m 2 ⌉ , m ] [\lceil \frac{m}{2}\rceil, m] [⌈2m⌉,m];(节点的子树个数与关键字个数相等)
- 所有叶节点包含全部关键字及指向相应记录的指针,叶节点中将关键字按大小顺序排列,并且相邻叶节点按大小顺序相互链接起来(支持顺序查找)
- 所有分支节点中仅包含它的各个子节点中关键字的最大值及指向其子节点的指针
- B+树中,无论查找成功与否,最终一定都要走到最下面一层节点(对比B树的查找,查找成功情况下,可能停在任何一层)
- B+树中,非叶节点不含有该关键字对应记录的存储地址,因此可以使一个磁盘块包含更多个关键字,使得B+树的阶更大,树高更矮,读磁盘次数更少,查找更快。典型应用如关系型数据库的“索引”(如MySQL)
二者对比
| - | B树 | B+树 |
|---|---|---|
| 关键字数与子树数 | 节点中的n个关键字对应n+1棵子树 | 节点中的n个关键字对应n棵子树 |
| 节点的关键字数范围 | 根节点的关键字数:[1, m-1],其他节点的关键字数[ ⌈ m 2 ⌉ \lceil\frac{m}{2}\rceil ⌈2m⌉-1, m-1] | 根节点的关键字数:[1, m],其他节点的关键字数[ ⌈ m 2 ⌉ \lceil\frac{m}{2}\rceil ⌈2m⌉, m] |
| 节点重复性 | 各节点中包含的关键字是不重复的 | 叶节点包含全部关键字,非叶节点中出现过的关键字也会出现在叶节点中 |
| 节点的作用 | B树的节点中都包含了关键字对应的记录的存储地址 | 叶节点包含信息,所有非叶节点仅起索引作用,非叶节点中的每个索引项只含有对应子树的最大关键字和指向该子树的指针 |
| 来源 | m阶B树是二叉查找树的进化 | m阶B+树是分块查找的进化(进化为多级分块查找) |
| 查找方式 | 不支持顺序查找,查找成功时,可能停在任何一层节点,查找速度不稳定 | 支持顺序查找,查找成功或失败都会到达最下一层节点,查找速度稳定 |
相同点:
- 除根节点外,都最少 ⌈ m 2 ⌉ \lceil\frac{m}{2}\rceil ⌈2m⌉个分叉(确保节点不要太空)
- 任何一个节点的子树都一样高(确保“绝对平衡”)
- 二者都是用于文件系统:
- B树主要用作文件的索引,因此它的查找涉及外存的存取。具体来讲,在B树上进行查找包含两种基本操作:
- 1)在B树中找节点:由于B树通常存储在磁盘上,因此查找操作1)是在磁盘上进行的
- 2)在节点中找关键字:这一查找操作是在内存中进行的,即在磁盘上找到指针p所指节点后,先将节点中的信息读入内存,然后再利用顺序查找或折半查找查询等于K的关键字
- 显然在磁盘上进行一次查找比在内存中进行一次查找耗费时间更多,因此在磁盘上进行查找的次数(即待查关键字所在节点在B树上的层次数)是决定B树查找效率的首要因素
- B+树是应文件系统所需而出的一种B树的变型树
- B树主要用作文件的索引,因此它的查找涉及外存的存取。具体来讲,在B树上进行查找包含两种基本操作:
