03、K-means聚类实现步骤与基于K-means聚类的图像压缩（1）

03、K-means聚类实现步骤与基于K-means聚类的图像压缩（1）

03、K-means聚类实现步骤与基于K-means聚类的图像压缩（1）
03、K-means聚类实现步骤与基于K-means聚类的图像压缩（2）

开始学习机器学习啦，已经把吴恩达的课全部刷完了，现在开始熟悉一下复现代码。对这个手写数字实部比较感兴趣，作为入门的素材非常合适。

K-means聚类实现步骤

1、K-means基础

K-means算法是一种常用的聚类算法，它的实现步骤如下：

STEP1:从数据集中随机选择k个样本作为初始聚类中心。
STEP2:计算每个样本到各聚类中心的距离，并将样本归入最近的聚类中心。
STEP3:重新计算每个聚类的中心，该中心为该类所有样本的平均值。
STEP4:重复步骤2和3，直到满足以下条件之一：

聚类中心不再变化。
达到预设的最大迭代次数。
最小平方误差SSE（误差的平方和）达到预设的阈值。

2、K-means的底层代码实现

STEP0:调用numpy和绘图库：

import numpy as np
from matplotlib import pyplot as plt

STEP1:从数据集中随机选择k个样本作为初始聚类中心：

# 随机初始化聚类初始优化点
def kMeans_init_centroids(X, K):
    # 随机重新排序样本的索引
    randidx = np.random.permutation(X.shape[0])
    # 取前K个样本作为聚类中心
    centroids = X[randidx[:K]]
    return centroids

STEP2:计算每个样本到各聚类中心的距离，并将样本归入最近的聚类中心：

def find_closest_centroids(X, centroids):
    # 获取聚类中心的数量，也即K值
    K = centroids.shape[0]
    # 初始化一个数组用于存储每个样本所属的聚类中心的索引  
    idx = np.zeros(X.shape[0], dtype=int)
    # 遍历数据集中的每个样本
    for i in range(X.shape[0]):
        # 初始化一个列表用于存储当前样本到每个聚类中心的距离
        distance = []
        # 计算当前样本到每个聚类中心的距离
        for j in range(centroids.shape[0]):
            # 使用欧几里得距离公式计算样本i与聚类中心j之间的距离
            norm_ij = np.linalg.norm(X[i] - centroids[j])
            distance.append(norm_ij)
            # 找出距离列表中的最小值，该最小值对应的索引就是当前样本所属的聚类中心
        idx[i] = np.argmin(distance)
        # 返回每个样本所属的聚类中心的索引数组
    return idx

STEP3:重新计算每个聚类的中心，该中心为该类所有样本的平均值：

def compute_centroids(X, idx, K):
    # 获取数据集X的行数m和列数n  
    # m表示样本数量，n表示每个样本的特征数量  
    m, n = X.shape
    # 初始化一个K x n的零矩阵，用于存储K个聚类中心  
    # K表示聚类数量，n表示特征数量  
    centroids = np.zeros((K, n))
    # 遍历每个聚类中心  
    for k in range(K):
        # 从数据集X中选择属于当前聚类k的所有样本  
        # idx是一个长度为m的数组，存储了每个样本所属的聚类中心的索引  
        points = X[idx == k]
        # 计算属于当前聚类k的所有样本的平均值，得到聚类中心  
        # axis=0表示按列计算平均值  
        centroids[k] = np.mean(points, axis=0)
        # 返回计算得到的K个聚类中心  
    return centroids

STEP4:重复步骤2和3，直到满足以下条件之一：
聚类中心不再变化。
达到预设的最大迭代次数。
最小平方误差SSE（误差的平方和）达到预设的阈值。
此处直接以达到预设的最大迭代次数作为停止条件

def run_kMeans(X, initial_centroids, max_iters=10):
    # 获取数据集X的行数m和列数n
    # m表示样本数量，n表示每个样本的特征数量
    m, n = X.shape
    # 获取初始聚类中心的数量K
    K = initial_centroids.shape[0]
    # 将初始聚类中心赋值给centroids变量
    centroids = initial_centroids
    # 将初始聚类中心复制给previous_centroids变量，用于后续比较聚类中心是否发生变化
    previous_centroids = centroids
    # 初始化一个长度为m的零数组，用于存储每个样本所属的聚类中心的索引
    idx = np.zeros(m)
    # 开始运行K-means算法，最多迭代max_iters次
    for i in range(max_iters):
        # 输出当前迭代进度
        print("K-Means iteration %d/%d" % (i, max_iters - 1))
        # 调用find_closest_centroids函数，为数据集X中的每个样本找到最近的聚类中心，并返回索引数组
        idx = find_closest_centroids(X, centroids)
        # 调用compute_centroids函数，根据每个样本所属的聚类中心和索引数组，计算新的聚类中心
        centroids = compute_centroids(X, idx, K)
        # 返回最终的聚类中心和每个样本所属的聚类中心的索引
    return centroids, idx

3、K-means的底层代码案例

此处直接使用吴恩达的案例，非常简洁直观嘞：

import numpy as np
import matplotlib.pyplot as plt


def load_data():
    X = np.load("K_means_data/ex7_X.npy")
    return X


def draw_line(p1, p2, style="-k", linewidth=1):
    plt.plot([p1[0], p2[0]], [p1[1], p2[1]], style, linewidth=linewidth)


def plot_data_points(X, idx):
    # plots data points in X, coloring them so that those with the same
    # index assignments in idx have the same color
    plt.scatter(X[:, 0], X[:, 1], c=idx)


def plot_progress_kMeans(X, centroids, previous_centroids, idx, K, i):
    # Plot the examples
    plot_data_points(X, idx)

    # Plot the centroids as black 'x's
    plt.scatter(centroids[:, 0], centroids[:, 1], marker='x', c='k', linewidths=3)

    # Plot history of the centroids with lines
    for j in range(centroids.shape[0]):
        draw_line(centroids[j, :], previous_centroids[j, :])

    plt.title("Iteration number %d" % i)

def find_closest_centroids(X, centroids):
    """
    Computes the centroid memberships for every example
    Args:
        X (ndarray): (m, n) Input values
        centroids (ndarray): k centroids
    Returns:
        idx (array_like): (m,) closest centroids
    """
    # Set K
    K = centroids.shape[0]
    # You need to return the following variables correctly
    idx = np.zeros(X.shape[0], dtype=int)
    for i in range(X.shape[0]):
        # Array to hold distance between X[i] and each centroids[j]
        distance = []
        for j in range(centroids.shape[0]):
            norm_ij = np.linalg.norm(X[i] - centroids[j])
            distance.append(norm_ij)
        idx[i] = np.argmin(distance)
    return idx

# GRADED FUNCTION: compute_centpods
def compute_centroids(X, idx, K):
    """
    Returns the new centroids by computing the means of the
    data points assigned to each centroid.
    Args:
        X (ndarray):   (m, n) Data points
        idx (ndarray): (m,) Array containing index of closest centroid for each
                       example in X. Concretely, idx[i] contains the index of
                       the centroid closest to example i
        K (int):       number of centroids
    Returns:
        centroids (ndarray): (K, n) New centroids computed
    """
    # Useful variables
    m, n = X.shape
    # You need to return the following variables correctly
    centroids = np.zeros((K, n))
    for k in range(K):
        points = X[idx == k]
        centroids[k] = centroids[k] = np.mean(points, axis=0)
    return centroids


# You do not need to implement anything for this part
def run_kMeans(X, initial_centroids, max_iters=10, plot_progress=False):
    """
    Runs the K-Means algorithm on data matrix X, where each row of X
    is a single example
    """
    # Initialize values
    m, n = X.shape
    K = initial_centroids.shape[0]
    centroids = initial_centroids
    previous_centroids = centroids
    idx = np.zeros(m)
    # Run K-Means
    for i in range(max_iters):
        # Output progress
        print("K-Means iteration %d/%d" % (i, max_iters - 1))
        # For each example in X, assign it to the closest centroid
        idx = find_closest_centroids(X, centroids)
        # Optionally plot progress
        if plot_progress:
            plot_progress_kMeans(X, centroids, previous_centroids, idx, K, i)
            previous_centroids = centroids
        # Given the memberships, compute new centroids
        centroids = compute_centroids(X, idx, K)
    plt.show()
    return centroids, idx


# Load an example dataset
X = load_data()
# Set initial centroids
initial_centroids = np.array([[3,3],[6,2],[8,5]])
K = 3
# Number of iterations
max_iters = 10
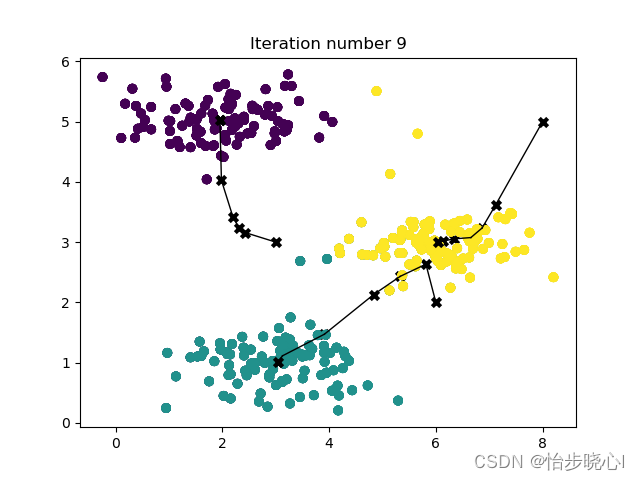
centroids, idx = run_kMeans(X, initial_centroids, max_iters, plot_progress=True)

运行结果：