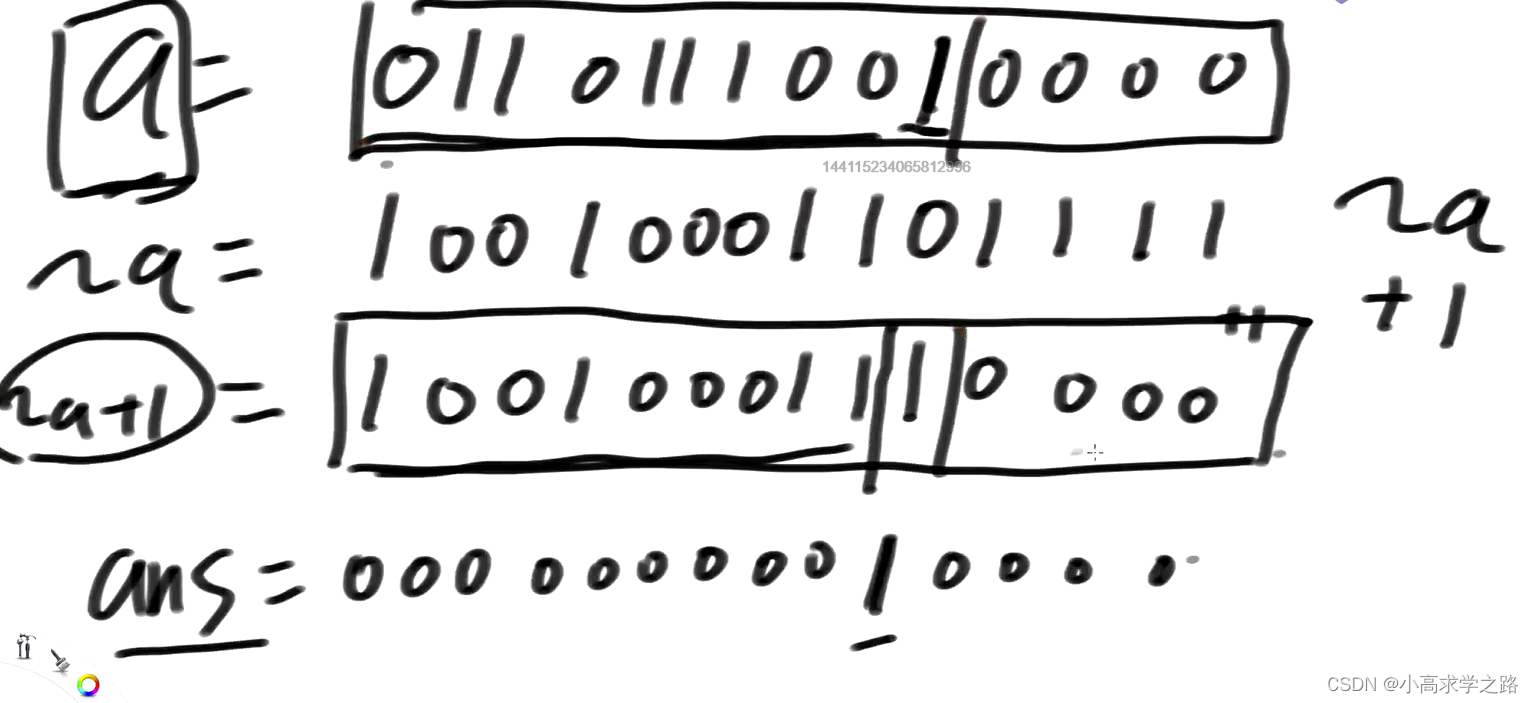当前位置：首页 > article >正文

时间复杂度和运算

article 2024/11/15 5:49:26

时间复杂度

在算法和数据结构中，有许多时间复杂度比 O(1) 更差的情况。以下是一些常见的时间复杂度，按照从最优到最差的顺序排列：

O(1)： 常数时间复杂度，操作的运行时间与输入规模无关，是最理想的情况。
O(log n)： 对数时间复杂度，常见于分治算法和二分搜索等。
O(n)： 线性时间复杂度，操作的运行时间与输入规模成正比。
O(n log n)： 线性对数时间复杂度，常见于一些高效的排序算法，如快速排序和归并排序。
O(n^2)： 平方时间复杂度，常见于一些简单的嵌套循环算法-选择,冒泡,插入
O(n^k)： 多项式时间复杂度，其中 k 是常数，通常表示更高次幂的多项式时间复杂度。
O(2^n)： 指数时间复杂度，常见于一些指数级增长的问题，如穷举搜索。
O(n!)： 阶乘时间复杂度，通常表示在排列组合问题中的情况。时间复杂度表示形式

对应的"选泡插"排序时间复杂度都是O(n^2)空间复杂度是O(1)

冒泡排序

时间复杂度:有两个for循环,第一个for循环是每个元素都要与其他的元素比较一遍,所以如果有N个元素,那么最外层的for循环的时间复杂度就是O(N),然后每一次外层的for循环,都会在内部的for循环中两两进行比较,又是O(N),因为是for循环嵌套.所以最后的时间复杂度就是O(n^2),空间复杂度的话-一般来说,除了用户要求的内存空间之外,额外申请的新的空间,则就是空间复杂度,这里用了一个temp临时变量来存储数据,所以该空间复杂度是O(1)


public class 冒泡排序 {

    public static void main(String[] args) {
        int arr[] = {1, 2, 4, 5, 3, 6, 8, 7};
        //第一层for循环代表的是轮数,从第一个数开始,每个数都要和其他的数进行比较,所以有多少数,总共就有多少轮
        for (int i = 0; i < arr.length; i++) {
            //第二层for循环代表的是如果是逆序则换位置,因为有j+1 为了防止下标越界,所以在第二层for循环的时候,在减1
            for (int j=0;j<arr.length-i-1;j++){
                    if (arr[j]>arr[j+1]){
                        int tepm =arr[j];
                        arr[j]=arr[j+1];
                        arr[j+1]=tepm;
                    }
            }
        }
        for (int i : arr) {
            System.out.print(i);
        }
    }


}

选择排序

package 算法;
public class 选择排序 {
    //先在[0~n-1]下标范围内找到最小值放到0位置上；
    //再在[1~n-1]下标范围内找到最小值放到1位置上；
    //依次如此操作，直到最后一个最小值【最大值】放在n-1位置上，完成排序操作；
    public static void main(String[] args) {
        int arr[] = {2, 1, 4, 5, 3, 6, 8, 7};

        for (int i = 0; i < arr.length-1; i++) {
            int minIndex=i;//最小值的下标设为第一个数的下标索引
            //然后第一个数和第二个数开始进行比较,看哪个数是最小的, 如果哪个是最小的,则记住最小值的下标,然后两个数进行交换,直到和其他的元素都比较完后,在走下一个数(也就是第一层for循环)
            for (int j=i+1;j<arr.length;j++){
                minIndex=arr[j]<arr[minIndex]?j:minIndex;
            }
            //交换位置
            int temp =arr[i];
            arr[i]=arr[minIndex];
            arr[minIndex]=temp;

        }
        for (int i : arr) {
            System.out.print(i);
        }
    }


}

插入排序

public class 插入排序 {
    //思路就是:默认第一个数的位置已经确定.从第二个位置开始,如果比第一个位置的数小,则换位置,
    //第三个数再和第二个数比较,如果小于第二个数,则换位置,否则不换,然后继续和第一个位置上的数进行比较,小于则换位置.否则不换, 以此类推
    public static void main(String[] args) {
        int arr[] = {2, 1, 4, 5, 3, 6, 8, 7};
        for (int i = 1; i < arr.length; i++) {
            for(int j=i-1;j>=0&&arr[j]>arr[j+1];j--){
                int temp=arr[j];
                arr[j]=arr[j+1];
                arr[j+1]=temp;
            }
        }
        for (int i : arr) {
            System.out.print(i);
        }
    }
}

运算

异或 (^)

不同为1,相同为0 有两个特性: a^0=a a^a=0

例题1:

a=1 ,b=2 在不使用第三个临时变量来完成两个数的交换,这里就可以用到异或方法

package 算法;

/**
 * @author : gaoPengShuai
 * @date : 2023/11/21 21:21
 * @modyified By :
 */
public class 异或 {
    public static void main(String[] args) {
        int a =1;
        int b=2;
        System.out.println("交换之前a的值是:"+a+" b的值是:"+b);
        //在不使用第三个变量来完成两个数的交换
        a=a^b;
        b=a^b;
        a=a^b;
        System.out.println("交换之后a的值是:"+a+" b的值是:"+b);
    }
}

运行结果:

交换之前a的值是:1 b的值是:2
交换之后a的值是:2 b的值是:1

Process finished with exit code 0

例题2:

在一个数组中,一个数出现了奇数次,其他的数出现了偶数次.找到该出现奇数次的数

    public static void  test1(){
      //在一个数组中,一个数出现了奇数次,其他的数出现了偶数次.找到该出现奇数次的数
        int arr[] ={1,2,3,2,3,3,1};
        int temp =0;
        for (int i : arr) {
            temp^=i;
        }
        System.out.println(temp);
    }

注意:这两个例题就用到了,a^a=0 然后0^b=b的方法,直接将两个数进行交换,但是值得注意的是,a和b值可以相同,但是内存地址不能相同,因为自己异或自己的结果是0,会将之前的值覆盖为0

例题3:

找到一个数转为二进制后,提取出最右侧的1

    public static void  test3(){
        //找到一个数转为二进制后,提取出最右侧的1
        int a=5;
        int eor=a &(-a);//也可以写成 a&(~a+1)

        System.out.println("值是:"+eor);
    }

运行结果:
值是:1