C++数据结构:图
目录
一. 图的基本概念
二. 图的存储结构
2.1 邻接矩阵
2.2 邻接表
三. 图的遍历
3.1 广度优先遍历
3.2 深度优先遍历
四. 最小生成树
4.1 最小生成树获取策略
4.2 Kruskal算法
4.3 Prim算法
五. 最短路径问题
5.1 Dijkstra算法
5.2 Bellman-Ford算法
5.3 Floyd-Warshall算法
六. 总结
一. 图的基本概念
图是一种由顶点集合以及顶点与顶点之间关系组成的数据结构,记为:G = { V, E }。
- 顶点集合V={x|x属于某个有穷非空集合}
- E = {(x,y)|x,y属于V}或者E={<x,y>|x,y属于V && Path(x,y)},其中(x,y)表示顶点x和y之间相连接,没有方向,<x,y>表示x连接到y,有方向。
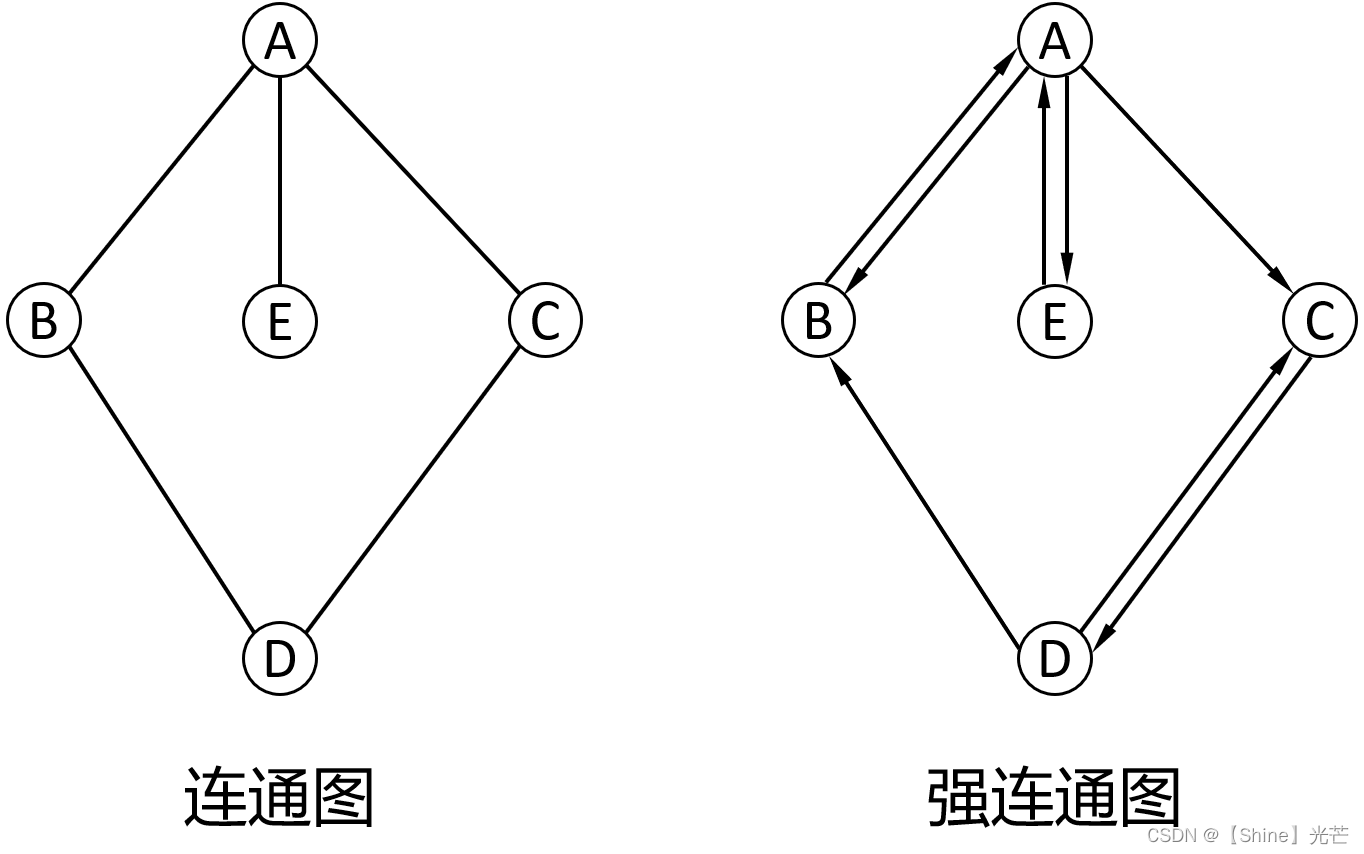
如图1.1所示,A、B、C、D称之为顶点,连接顶点之间的“线”称其为边,边的箭头表示连接方向,图1.1左边的A->B连接线表示A连接到B,有方向,记为<A,B>,右边图结构中A-B表示A和B相连接,没有方向,记为(A,B)。
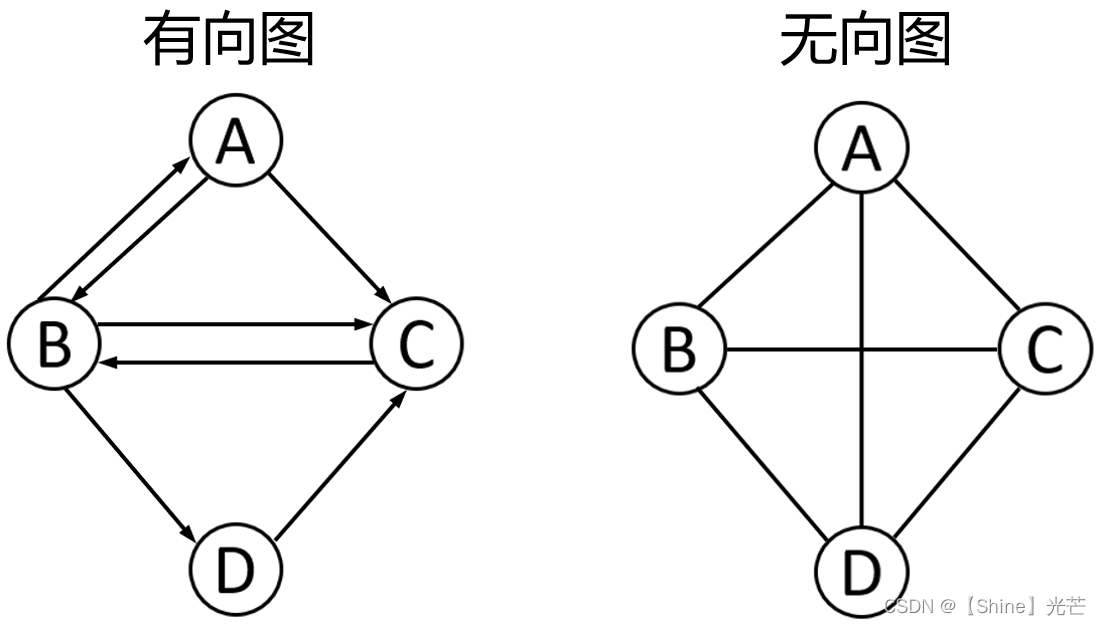
有向图与无向图:有向图中的顶点和顶点之间的连接具有方向性,如图1.1中左侧图结构所示,可以说顶点B连接到顶点D,但不可以说顶点D连接到顶点B,这是有向图结构。图1.1右侧的图结构是无向图,A和B之间有边相连,那我们可以认为A能够连接到B,B也能够连接到A。
完全图:在无向图中,假设顶点数量为N,那么有N*(N-1)/2,条边,即任意两个顶点之间都有边相连,那么就称其为无向完全图。在有向图中,任意两个顶点之间都有两条指向相反的连接线,即有N个顶点的有向图有N*(N-1)条边,称这样的图结构为有向完全图。

邻接顶点:在无向图中,如果(A,B)是一条边,那么我们称顶点A和顶点B邻接,在有向图中,如果<A,B>是一条边,则表示A连接到B,称顶点A邻接到顶点B,顶点B邻接自顶点A。
顶点的度:顶点的度指的是与顶点相连的边的条数,记为deg(V),表示顶点V的度。对于有向图,顶点V的度等于入度和出度之和,顶点V的出度指的是以V为起点的边的条数,记为outdev(V),顶点V的入度指以V为终点的边的条数,记为indev(V),那么deg(V) = outdev(V) + indev(V)。对于无向图,顶点的度与其出度和入度都相等,即deg(V) = outdev(V) = indev(V)。
路径:对于图G = { V, E },假设从顶点vi出发,经过一定的路径可以到顶点vj,那么从顶点vi到顶点vj所经过的顶点就称为顶点vi到顶点vj的路径。
路径长度:对于不带权的图,路径长度就是从源顶点到目标顶点所经过的边的条数,对于带权值的图,从源顶点到目标顶点的路径长度就是每条边的权值之和。如图1.3所示,所谓权值,就是边的附属信息。
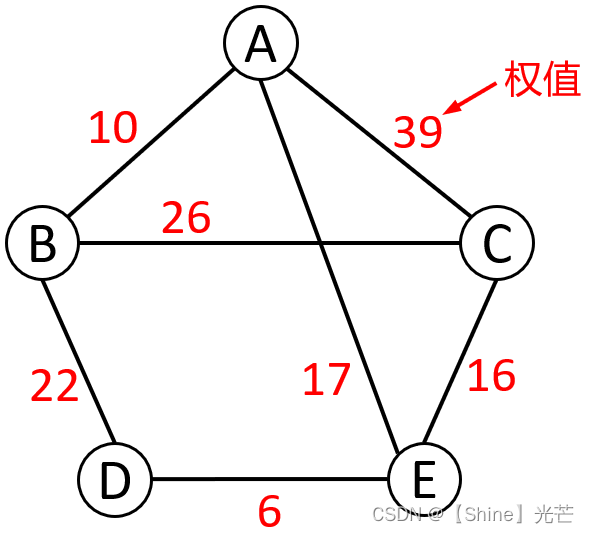
简单路径与回路:假设顶点v1和vm相连,路径v1, v2, ... , vm没有重复的顶点,那么称v1, v2, ... , vm为简单路径,如果v1,v2, ..., v1,路径从起始点开始又回到了起始点,那么就是回路。
子图:对于图G = { V, E},有图G1 = { V1, E1 },且有:V1为V的子集,E1为E的子集,那么称G1为G的子图。
连通图:在无向图中,如果顶点vi与顶点vj之间能够通过一些边连接起来,那么称顶点vi与顶点vj是连通的,如果无向图中任意一对顶点都是连通的,那么称这种图结构为连通图。
强连通图:在有向图中,如果对于任意一对顶点vi和vj,既有从vi到vj的路径,也有从vj到vi的路径,那么这种图结构称为强连接图。
最小生成树:对于连通图,能够将每个顶点连接在一起的最小连通子图,称为最小生成树,对于有N个顶点的连通图,其最小生成树应该有N-1条边。
二. 图的存储结构
图的存储结构有两种:邻接矩阵和邻接表。
2.1 邻接矩阵
所谓邻接矩阵,就是一个二维数组。假设使用一维数组存储图中的每一个顶点,每一个顶点都有一个与之对应的在数组中的下标,将这个一维数组拓展到二维数组,就可以表示顶点和顶点之间的连接关系。假设邻接矩阵为M,那么M[i][j]就表示下标i对应的顶点和下标j对应的顶点的连接关系。
对于不带权值的图,如果矩阵中两个顶点相连接,即vi与vj相连,那么邻接矩阵中的M[i][j]=1,对于带权值的图,邻接矩阵中的值表示每条边的权重,如果两条边不相连,那么对应的邻接矩阵中的值就记为无穷大。对于无向图的邻接矩阵,是关于主对角线对称的矩阵。
邻接矩阵的优缺点:邻接矩阵能够快速查找两个顶点是否直接相连,但是如果边较少的时候,邻接矩阵中会有大量的浪费空间,且使用邻接矩阵不容易求得两个顶点之间的路径。

代码2.1为使用邻接矩阵进行存储的图结构的模板类代码实现。该类为模板类,模板参数有四个分别为:V表示图的顶点数据类型、W表示权值数据类型、MAX_W表示两顶点不相连时默认的权重,Direction表示该图是有向图还是无向图。
成员变量有三个:_vertex为记录顶点数据的一维数组,_valIndexMap为顶点数据与下标的映射哈希表,_edges为邻接矩阵。
先实现构造函数和顶点边添加函数,在构造函数中,应当将数组中给出的全部数据插入到_vertex中去,并且构造数据值和_vertex数组下标的映射关系。在边添加函数_AddEdges中,要传三个参数,分别为源顶点、目标顶点和权值,获取源顶点和目标顶点的下标,在临界矩阵中建立源顶点到目标顶点的连接,如果是无向图还要添加目标顶点到源顶点的连接。
为了方便观察,引入Print函数用于向屏幕打印邻接矩阵,以检查结果的正确性。
代码2.1:邻接矩阵存储图
#include <iostream>
#include <vector>
#include <unordered_map>
#include <cassert>
namespace Matrix
{
template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>
class Graph
{
public:
// 构造函数,传递一维数组和数据个数
Graph(const V* arr, size_t size)
{
for (size_t i = 0; i < size; ++i)
{
_vertex.push_back(arr[i]);
_valIndexMap[arr[i]] = i;
}
// 为邻接矩阵申请空间并初始化
_edges.resize(size, std::vector<W>(size, MAX_W));
}
// 顶点下标获取函数
size_t GetIndex(const V& val)
{
auto pos = _valIndexMap.find(val);
if (pos != _valIndexMap.end())
{
return pos->second;
}
else
{
assert(false);
return -1;
}
}
// 边添加函数
void AddEdge(const V& src, const V& dst, const W& w)
{
// 获取源顶点和目标顶点对应的一维数组下标
size_t srci = GetIndex(src);
size_t dsti = GetIndex(dst);
// 建立srci->dsti的连接关系
_edges[srci][dsti] = w;
// 如果是无向图,还需要建立dst->src的连接关系
if (Direction == false)
{
_edges[dsti][srci] = w;
}
}
// 邻接矩阵打印函数
void Print()
{
size_t n = _vertex.size();
for (size_t i = 0; i < n; ++i)
{
for (size_t j = 0; j < n; ++j)
{
if (_edges[i][j] == MAX_W) std::cout << "* ";
else std::cout << _edges[i][j] << " ";
}
std::cout << std::endl;
}
}
private:
std::vector<V> _vertex; // 存储顶点值的一维数组
std::unordered_map<V, size_t> _valIndexMap; // 顶点值与其在数组下标中的映射关系
std::vector<std::vector<W>> _edges; // 邻接矩阵
};
}2.2 邻接表
邻接表,就是对图中每一个顶点,都分配一个链表,链表中的每个顶点都表示一个与该顶点直接相连的顶点,如图2.2就是邻接表存储存储图的示意。对于无向图,只需要一张邻接表就能够清楚表示图结构。对于有向图,可以使用一张出边表和一张入边表,出边表记录以每个顶点为起始点的边连接到的顶点,入边表记录以每个顶点为终点的边的起始顶点,在实际应用中,使用一张出边表也能清晰表达有向图的结构,因此入边表一般省略。
使用邻接表的优缺点:邻接表适用于存储稀疏图,适用于查找一个顶点连接出去的边,但是无法像邻接矩阵那样以O(1)的时间复杂度判断两个顶点是否直接相连。
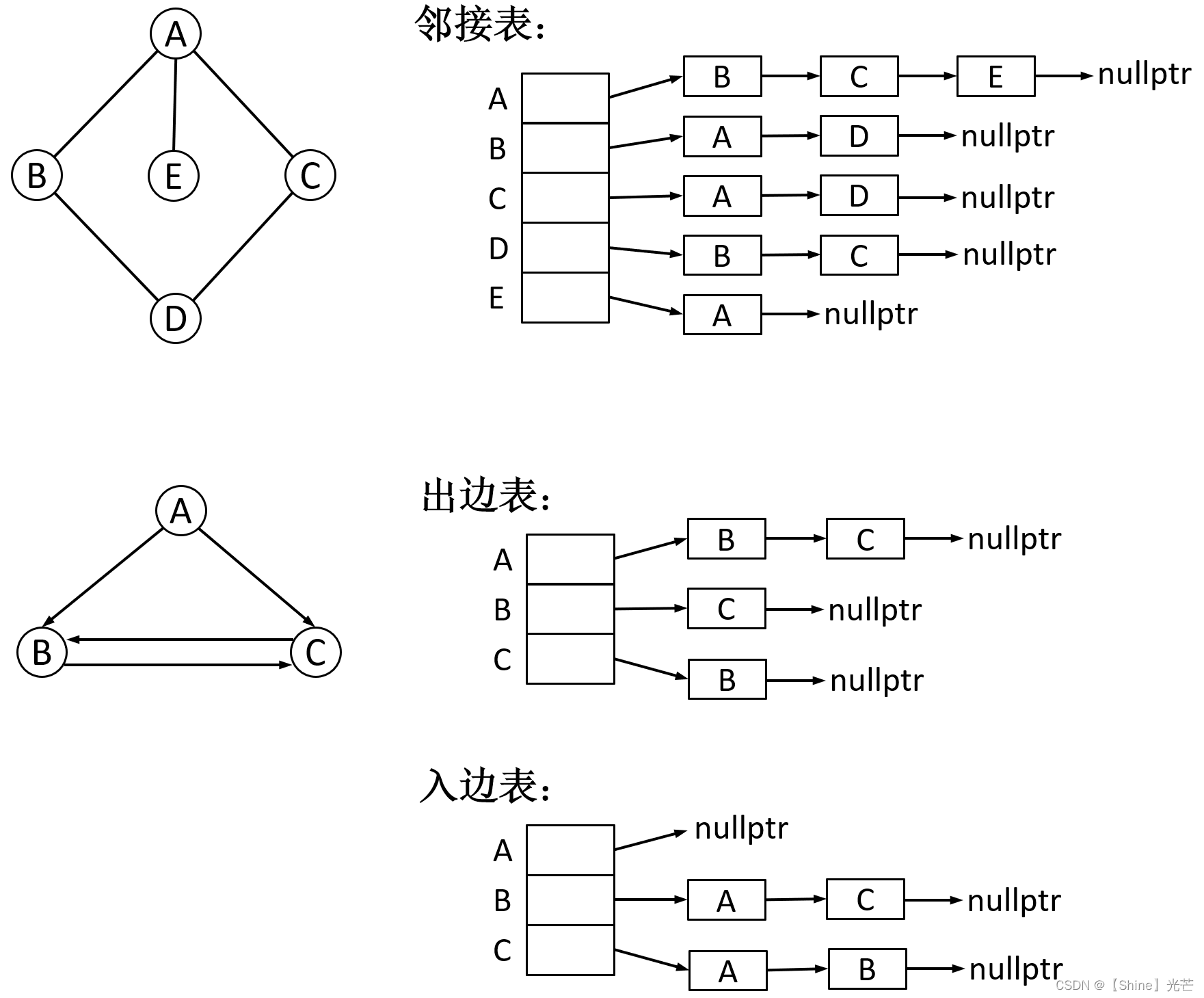
代码2.2对邻接表存储的图结构进行了初步的实现,定义struct Edge结构体来存储边,struct Edge包含三个成员:目标顶点下标_dsti、权值_w、下一个顶点_next。模板类class Graph的成员变量与邻接矩阵版的基本相同,区别就在于使用邻接表表示顶点间的连接关系,添加边函数AddEdge将新的连接边new出来的struct Edge对象头插到对应单链表处即可。
代码2.2:采用邻接表存储图
#include <iostream>
#include <vector>
#include <unordered_map>
#include <cassert>
namespace LinkTable
{
template<class W>
struct Edge
{
size_t _dsti; // 目标顶点在数组中的下标
W _w; // 权重
struct Edge* _next; // 单链表下一个顶点
// 构造函数
Edge(size_t dsti, const W& w)
: _dsti(dsti), _w(w), _next(nullptr)
{ }
};
template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>
class Graph
{
typedef Edge<W> Edge;
public:
// 构造函数
Graph(const V* arr, size_t size)
{
// 将顶点插入一维数组,并建立顶点与下标的映射
for (size_t i = 0; i < size; ++i)
{
_vertex.emplace_back(arr[i]);
_valIndexMap[arr[i]] = i;
}
// 初始化邻接表
_edges.resize(size, nullptr);
}
// 顶点下标获取函数
size_t GetIndex(const V& val)
{
auto pos = _valIndexMap.find(val);
if (pos != _valIndexMap.end())
{
return pos->second;
}
else
{
assert(false);
return -1;
}
}
// 添加边函数
void AddEdge(const V& src, const V& dst, const W& w)
{
// 获取源节点和目标节点的下标
size_t srci = GetIndex(src);
size_t dsti = GetIndex(dst);
// 构建srci->dsti的连接关系
Edge* edge1 = new Edge(dsti, w);
edge1->_next = _edges[srci];
_edges[srci] = edge1;
// 如果是无向图,构建dsti->srci的连接关系
if (Direction == false)
{
Edge* edge2 = new Edge(srci, w);
edge2->_next = _edges[dsti];
_edges[dsti] = edge2;
}
}
// 打印邻接表函数
void Print()
{
size_t n = _edges.size();
for (size_t i = 0; i < n; ++i)
{
std::cout << _vertex[i] << ":";
Edge* cur = _edges[i];
while (cur)
{
std::cout << "[" << _vertex[cur->_dsti] << ":" << cur->_w << "]" << "->";
cur = cur->_next;
}
std::cout << "nullptr" << std::endl;
}
}
private:
std::vector<V> _vertex; // 存储顶点的一维数组
std::unordered_map<V, size_t> _valIndexMap; // 数据和下标的映射关系哈希表
std::vector<Edge*> _edges; // 邻接表表示的连接边
};
}三. 图的遍历
3.1 广度优先遍历
广度优先遍历,我们可以理解为分层遍历,依次遍历每一层的顶点数目。在具体实现中使用队列进行辅助,先将起始顶点入队列,从队头开始遍历,将与队头直接相连且还未被遍历的顶点插入队尾,每次插入一个顶点,都要对这个顶点进行记录,以避免重复遍历。图3.1为广度优先遍历的分层情况,第0层遍历完成后遍历第1层,之后是第2层、第3层,以此类推。代码3.1在使用邻接矩阵存储的图结构中,实现对图的广度优先遍历。

代码3.1:图的广度优先遍历
// 图的广度优先遍历,src为遍历起点
void BFS(const V& src)
{
size_t srci = GetIndex(src); // 起点下标
size_t n = _vertex.size(); // 顶点个数
std::vector<bool> visited(n, false); // 记录每个点是否被遍历(是否已经加入到队列中)
std::queue<size_t> q; // 队列记录顶点下标
q.push(srci); // 源顶点先入队列
visited[srci] = true; // 记录源顶点已被加入队列
size_t levelSize = 1; // 每层节点个数
size_t level = 0;
// 使用辅助队列,开始逐层执行广度优先遍历算法
while (!q.empty())
{
printf("第%u层:", level++);
for (size_t i = 0; i < levelSize; ++i)
{
size_t u = q.front();
q.pop();
std::cout << _vertex[u] << " ";
// 检查u->v的连接情况
// 如果u->v相连,且v尚未被遍历,那么v入队列
for (size_t v = 0; v < n; ++v)
{
if (_edges[u][v] != MAX_W && visited[v] == false)
{
visited[v] = true;
q.push(v);
}
}
}
std::cout << std::endl;
levelSize = q.size();
}
}3.2 深度优先遍历
深度优先,就是选定一个原点后,就一直向下递归遍历,直到无法递归的时候就回溯,直到完成对于所有点的遍历,通过vector数组记录每个点是否被遍历。

代码3.2:图的深度优先遍历算法
// 深度优先遍历算法子函数
// curi为当前遍历节点的下标,visited为记录节点是否被遍历过的数组
void _DFS(size_t curi, std::vector<bool>& visited)
{
visited[curi] = true;
std::cout << _vertex[curi] << std::endl;
// 检查是否有curi->u的连接
// 如果u还未被遍历,那么就递归遍历执行深度优先算法
for (size_t u = 0; u < _edges.size(); ++u)
{
if (_edges[curi][u] != MAX_W && visited[u] == false)
{
_DFS(u, visited);
}
}
}
// 深度优先遍历函数,src为起始点
void DFS(const V& src)
{
size_t srci = GetIndex(src); // 遍历源顶点下标
size_t n = _vertex.size(); // 顶点个数
std::vector<bool> visited(n, 0); // 记录每个节点是否被遍历过的数组
_DFS(srci, visited);
}四. 最小生成树
4.1 最小生成树获取策略
所谓最小生成树,是对于无向连通图的概念,即:路径权值和最小的、连通的子图。这就要求最小生成树满以下条件:
- 如果原图有N个顶点,那么其最小生成树有N-1条边。
- 最小生成树中的边不能构成回路。
- 必须是满足前两个条件,边权值和最小的生成树。
获取最小生成树的算法有Kruskal算法(克鲁斯卡尔算法)和Prim算法(普里姆算法),这两种算法都是采用“贪心”策略,即寻找局部最优解,即:当前图中满足一定条件的权值最小的边。但是要注意,Kruskal算法和Prim算法都是局部贪心算法,能够取得局部最优解,但是不一定获取的是全局最优解,它们获取的结果只能说是非常接近于最小生成树,而不一定就是最小生成树。
4.2 Kruskal算法
Kruskal算法的思想就是在整个图的所有边中,筛选出权值最小的边,同时在选边的过程中避免构成环,等到筛选出N-1条边后,就可以获取最小生成树。图4.1为Kruskal算法的选边过程,其中红色加粗的线为被选择的边。
Kruskal算法核心:每次都筛选权值最小的、且不构成回路的边,加入生成树。

通过Kruskal算法获取最小生成树需要使用 小根堆 + 并查集 来辅助进行,其中小根堆负责每次在所有尚未选取的边中筛选权值最小的边,并查集用于避免生成回路(环)。需要定义struct Edge类来记录边的属性信息,struct Edge的成员包括起始顶点下标srci、目标顶点下标dsti以及权重w,重载> 运算符,用于比较权重大小。在Kruskal算法的代码中首先要将所有的边插入小根堆,每次从堆顶拿出一条边,使用并查集检查两个顶点是否会构成环(属于同一个集合),如果不会构成环,那么就将这条边添加到生成树中去。之后,将此时的srci和dsti归并到并查集的同一集合中去以避免成环,然后选边计数器+1,进行权重累加。假设总共有N个顶点,如果选出生成树有N-1条边,说明成功获得了最小生成树,返回每个边的权重之和,否则就是获取最小生成树失败,返回MAX_W。
代码4.1为Kruskal算法及其配套被调函数及自定义类型的实现,其中Graph的其余不相关函数省略,代码4.2为并查集的实现代码。
代码4.1:Kruskal算法及其配套被调函数及自定义类型的实现
#include "UnionFindSet.hpp"
#include <iostream>
#include <vector>
#include <queue>
#include <unordered_map>
#include <algorithm>
#include <cassert>
namespace Matrix
{
// 自定义类型 -- 顶点与顶点之间的边
template<class W>
struct Edge
{
size_t _srci; // 源顶点下标
size_t _dsti; // 目标顶点下标
W _w; // 权重
// 构造函数
Edge(size_t srci, size_t dsti, const W& w)
: _srci(srci), _dsti(dsti), _w(w)
{ }
// 大于比较运算符重载函数,用于构建小根堆
bool operator>(const Edge<W>& w) const
{
return _w > w._w;
}
};
template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>
class Graph
{
typedef Edge<W> Edge;
typedef Graph<V, W, MAX_W, Direction> Self;
public:
// 强制生成默认构造函数
Graph() = default;
// ....
// 与Kruskal算法不相关的成员函数全部省略
// 根据下标添加边的函数
void _AddEdge(size_t srci, size_t dsti, const W& w)
{
_edges[srci][dsti] = w;
if (Direction == false)
{
_edges[dsti][srci] = w;
}
}
// Kruskal算法获取最小生成树
// 返回值为最小生成树的权值和,minTree为输出型参数,用于获取最小生成树
// 如果无法获取最小生成树,那么就返回MAX_W
W Kruskal(Self& minTree)
{
// 初始化minTree中的每个成员
size_t n = _vertex.size();
minTree._vertex = _vertex;
minTree._valIndexMap = _valIndexMap;
minTree._edges.resize(n, std::vector<W>(n, MAX_W));
// 将所有边的信息(源顶点、目标顶点、权值)插入到小根堆中去
std::priority_queue<Edge, std::vector<Edge>, std::greater<Edge>> minHeap;
for (size_t i = 0; i < n; ++i)
{
for (size_t j = i + 1; j < n; ++j)
{
if (_edges[i][j] != MAX_W)
{
Edge edge(i, j, _edges[i][j]);
minHeap.emplace(edge);
}
}
}
UnionFindSet ufs(n); // 用于避免构成回路的并查集
size_t count = 0; // 计数器,用于统计选取了多少条边
W totalW = W(); // 总权值计数器
std::cout << "Kruskal开始选边:" << std::endl;
while (!minHeap.empty())
{
// 小根堆堆顶为当前尚未被筛选且权值最小的边
size_t srci = minHeap.top()._srci;
size_t dsti = minHeap.top()._dsti;
size_t w = minHeap.top()._w;
minHeap.pop();
// 检查当前两个节点是否位于同一并查集的几何中
if (!ufs.InSet(srci, dsti))
{
std::cout << "[" << _vertex[srci] << "->" << _vertex[dsti] << "]:" << w << std::endl;
// 向最小生成树中添加srci->dsti的边
minTree._AddEdge(srci, dsti, w);
// 将srci和dsti归为同一集合
ufs.Union(srci, dsti);
// 选边计数器+1,权值累加
++count;
totalW += w;
}
else
{
std::cout << "构成环 " << "[" << _vertex[srci] << "->" << _vertex[dsti] << "]:" << w << std::endl;
}
}
// 如果选择了n-1条边,那么说明获取了最小生成树,否则获取最小生成树失败
if (count == n - 1) {
return totalW;
}
else {
return MAX_W;
}
}
private:
std::vector<V> _vertex; // 存储顶点值的一维数组
std::unordered_map<V, size_t> _valIndexMap; // 顶点值与其在数组下标中的映射关系
std::vector<std::vector<W>> _edges; // 邻接矩阵
};
}代码4.2:并查集(UnionFindSet.hpp头文件)
#pragma once
#include <vector>
#include <algorithm>
class UnionFindSet
{
public:
UnionFindSet(size_t n)
:_ufs(n, -1)
{}
void Union(int x1, int x2)
{
int root1 = FindRoot(x1);
int root2 = FindRoot(x2);
// 如果本身就在一个集合就没必要合并了
if (root1 == root2)
return;
// 控制数据量小的往大的集合合并
if (abs(_ufs[root1]) < abs(_ufs[root2]))
std::swap(root1, root2);
_ufs[root1] += _ufs[root2];
_ufs[root2] = root1;
}
int FindRoot(int x)
{
int root = x;
while (_ufs[root] >= 0)
{
root = _ufs[root];
}
// 路径压缩
while (_ufs[x] >= 0)
{
int parent = _ufs[x];
_ufs[x] = root;
x = parent;
}
return root;
}
// 检查两个节点是否属于同一集合
bool InSet(int x1, int x2)
{
return FindRoot(x1) == FindRoot(x2);
}
// 获取并查集中集合的数量
size_t SetSize()
{
size_t size = 0;
for (size_t i = 0; i < _ufs.size(); ++i)
{
if (_ufs[i] < 0)
{
++size;
}
}
return size;
}
private:
std::vector<int> _ufs;
};4.3 Prim算法
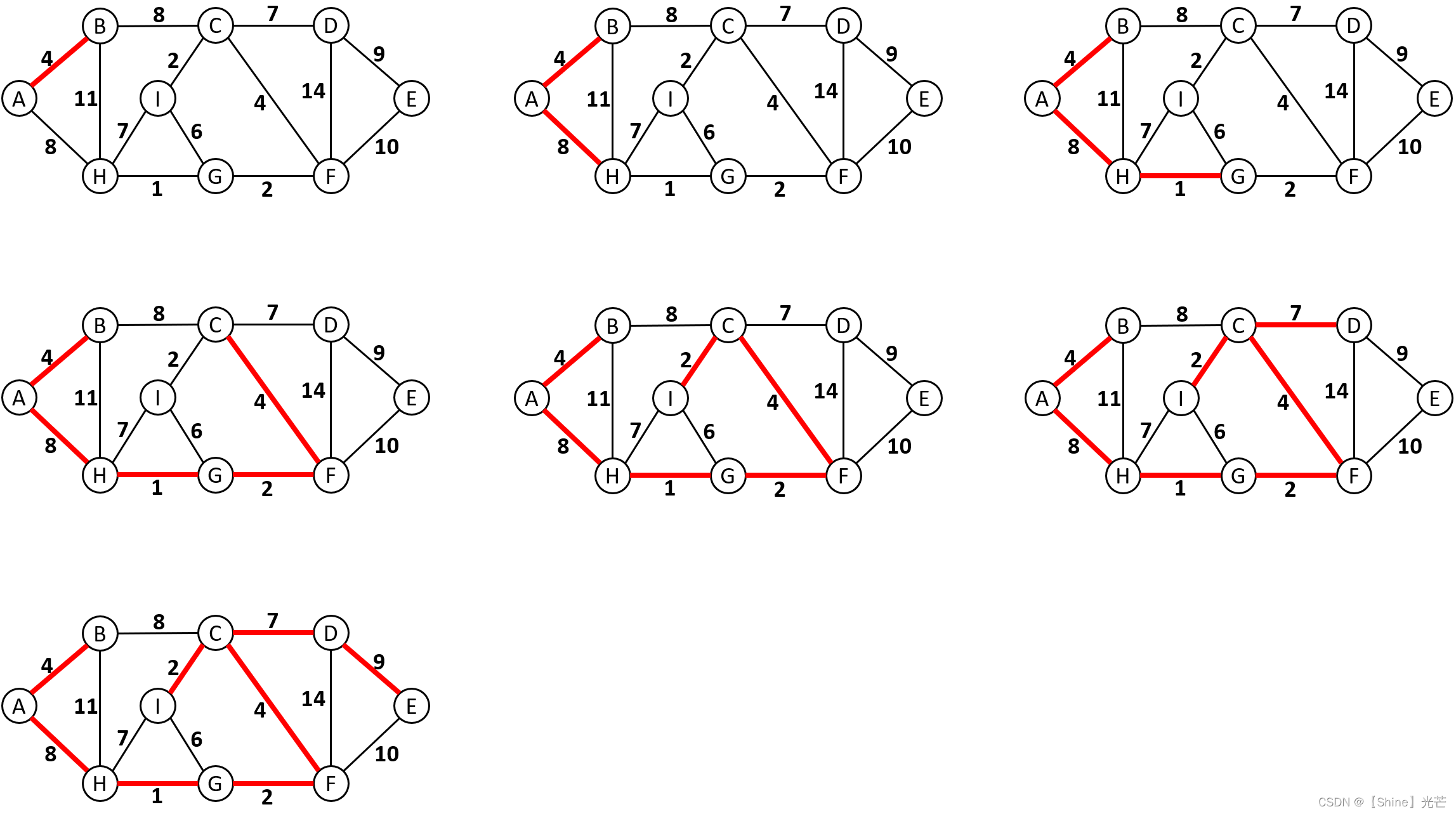
Prim算法(普里姆算法)的思路与Kruskal算法基本一致,采用的都是贪心策略,与Kruskal算法不同的是,Prim算法会选定一个起始点src,并将已经连通的顶点和尚未被连通的顶点划分到两个集合中去,分别记为S和U,每一次筛选,都会选出从si->ui的边中权值最小的那个,由于对已经连通和尚未连通的顶点进行了划分,因此选边建立连接的过程中不需要并查集来辅助就能够避免成环。图4.3为Prim算法的选边过程,红色加粗的实线为被选择的边。
代码4.3:Prim算法的实现
// Prim算法获取最小生成树
W Prim(const V& src, Self& minTree)
{
// 初始化minTree中的每个成员
size_t n = _vertex.size();
minTree._vertex = _vertex;
minTree._valIndexMap = _valIndexMap;
minTree._edges.resize(n, std::vector<W>(n, MAX_W));
// 起始节点对应下标
size_t srci = GetIndex(src);
// visited记录每个顶点是否已经被连通了起来
std::vector<bool> visited(n, false);
visited[srci] = true; // 源顶点自身连通
// 用于选取最短边的小根堆
std::priority_queue<Edge, std::vector<Edge>, std::greater<Edge>> minHeap;
// 将以srci为起点的边添加到小根堆中去
for (size_t i = 0; i < n; ++i)
{
if (_edges[srci][i] != MAX_W)
{
// Edge edge(srci, i, _edges[srci][i]);
// minHeap.push(edge);
minHeap.emplace(srci, i, _edges[srci][i]);
}
}
size_t count = 0; // 选边计数器
W totalW = W(); // 权值之和
std::cout << "Prim开始选边:" << std::endl;
// 开始依次选边
while (!minHeap.empty())
{
// 取当前边的起点为u,终点为v,权重为w
size_t u = minHeap.top()._srci;
size_t v = minHeap.top()._dsti;
W w = minHeap.top()._w;
minHeap.pop();
// 检查建立u->v的连接后,是否会构成环
if (visited[v] == false) // 不会构成环
{
std::cout << "[" << _vertex[u] << "->" << _vertex[v] << "]:" << w << std::endl;
// 在minTree中建立u->v的连接
minTree._AddEdge(u, v, w);
// 记顶点v被选取,选边计数器+1,权值累加
visited[v] = true;
++count;
totalW += w;
// 将以v为起点的边添加到小根堆minHeap中去
for (size_t k = 0; k < n; ++k)
{
if (visited[k] == false && _edges[v][k] != MAX_W)
{
// Edge edge(v, k, _edges[v][k]);
// minHeap.push(edge);
minHeap.emplace(v, k, _edges[v][k]);
}
}
}
else
{
std::cout << "构成环 " << "[" << _vertex[u] << "->" << _vertex[v] << "]:" << w << std::endl;
}
}
if (count + 1 == n) {
return totalW;
}
else {
return MAX_W;
}
}五. 最短路径问题
最短路径,就是计算从任意顶点vi到vj所经过的路径,权值和最小的那条路径。
5.1 Dijkstra算法
Dijkstra算法(迪杰斯特拉算法),用于求单源最短路径,即:给定一个起点,计算以这个顶点为起点,图中其余任意顶点为终点的路径中,权值之和最小的那一条路径。注意,Dijkstra算法要求不能带有负权值。
Dijkstra算法的核心思想是贪心算法,其大致的流程为:将一个有向图G中的顶点分为S和Q两组,其中S为已经确定了最短路径的顶点,Q为尚未确定最短路径的顶点,最初先将处源顶点srci以外所有顶点都加入Q,源顶点srci加入S。每次从Q中找出一个源顶点到该顶点最小的顶点u,将其从Q中移出放入到S中,对与u相邻的顶点v进行松弛操作。所谓松弛操作,就是比较srci->u + s->v的和是否比原来srci->v的路径和小,如果是,那么就更新srci->v的最短路径,反复进行松弛操作,直到Q集合中没有顶点。图5.1为Dijkstra算法松弛迭代的过程,黑色填充的顶点为已经确定最短路径的顶点,灰色填充为本轮遍历的源顶点。
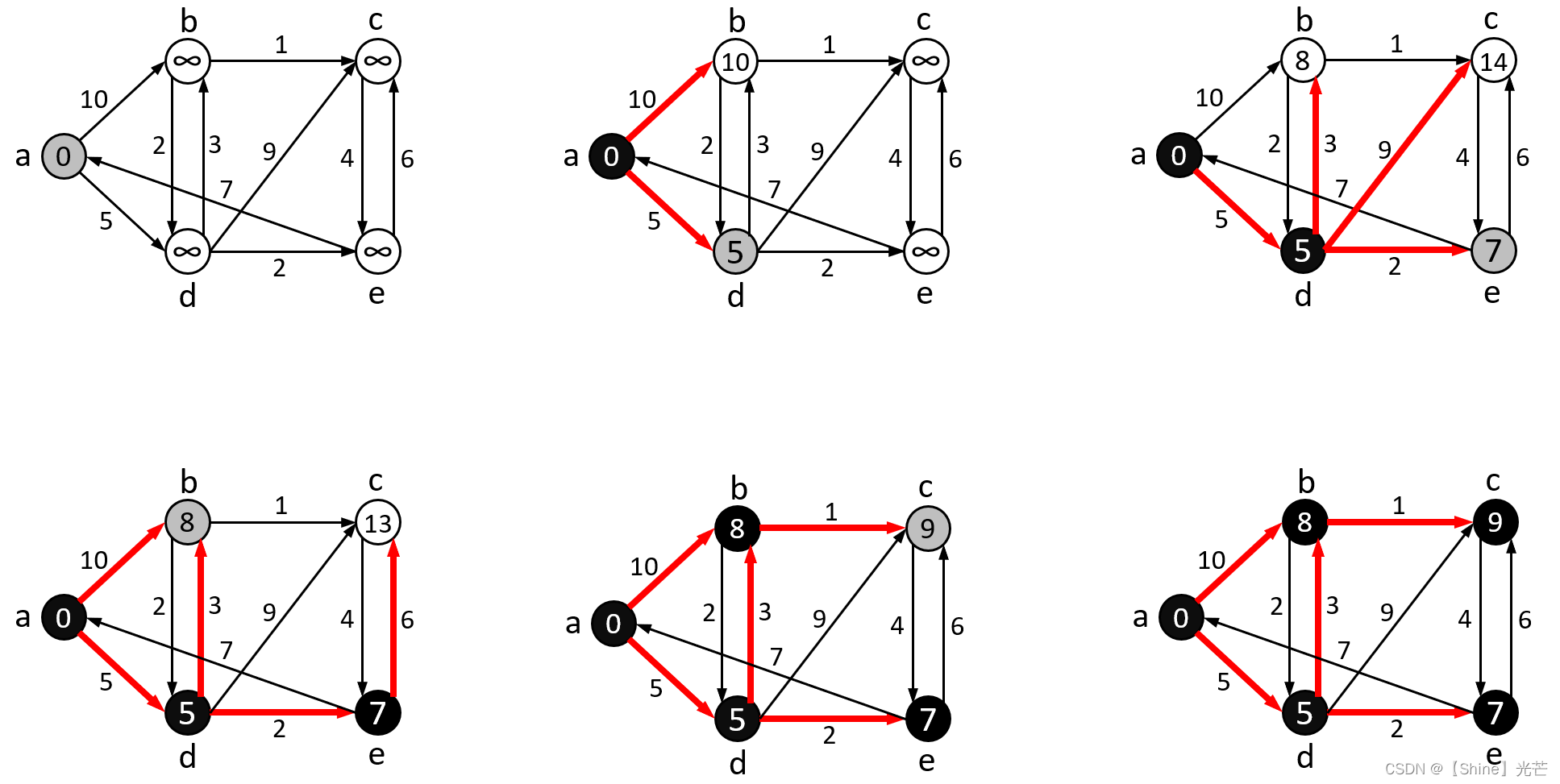
代码5.1为Dijkstra算法的具体实现,该函数接收三个参数,分别为起始点、最小路径dist(输出型参数)、每个顶点的父亲顶点pPath(输出型参数),这里使用pPath的目的是为了避免存储全部的路径,达到节省空间,降低算法编码难度的目的。为了观察结果,实现了PrintPath函数,用于打印顶点src到任意顶点的最短路径。
代码5.1:Dijkstra算法的实现
// Dijkstra求最小生成树
// dist为路径和,pPath为每个顶点前导顶点的下标
void Dijkstra(const V& src, std::vector<W>& dist, std::vector<size_t>& pPath)
{
// 初始化dist和pPath数组
size_t n = _vertex.size();
dist.resize(n, MAX_W);
pPath.resize(n, -1);
size_t srci = GetIndex(src); // 起始顶点的下标
dist[srci] = 0;
pPath[srci] = srci;
// visited数组记录每个顶点是否已经可以确定最短路径
std::vector<bool> visited(n, false);
// visited[srci] = true;
// 开始选边迭代
for (size_t k = 0; k < n; ++k)
{
// 挑选出尚未确定最短路径的顶点中,离srci最近的顶点,记下标为u
size_t u = -1;
W minDist = MAX_W;
for (size_t i = 0; i < n; ++i)
{
if (visited[i] == false && dist[i] < minDist)
{
u = i;
minDist = dist[i];
}
}
// 将u添加到已经确定最小路径和的集合中去
visited[u] = true;
// 检查u->v + dist[u]是否比原来的dist[v]小
// 如果小,那么更新dist[v]的值
for (size_t v = 0; v < n; ++v)
{
if (visited[v] == false && _edges[u][v] != MAX_W &&
dist[u] + _edges[u][v] < dist[v])
{
dist[v] = dist[u] + _edges[u][v];
pPath[v] = u;
}
}
}
}
// 路径打印函数
void PrintPath(const V& src, const std::vector<W>& dist, const std::vector<size_t>& pPath)
{
size_t srci = GetIndex(src);
size_t n = pPath.size();
for (size_t i = 0; i < n; ++i)
{
std::vector<int> path;
size_t parent = i;
while (pPath[parent] != parent)
{
path.push_back(parent);
parent = pPath[parent];
}
path.push_back(srci);
std::reverse(path.begin(), path.end());
for (const auto x : path)
{
std::cout << _vertex[x] << "->";
}
std::cout << "权重:" << dist[i] << std::endl;
}
}5.2 Bellman-Ford算法
Dijkstra算法不能解决带有负权的图的问题,为此,Bellman-Ford算法(贝尔曼-福特算法)被提了出来,这种算法可以解决带有负权的图的最小路径问题,这种算法也是用于解决单源最短路径问题的,即:给定一个起始点src,获取从src到每一个顶点的最短路径。
Bellman-Ford算法实际上是一种暴力求解的算法,对于有N个顶点的图,要暴力搜索顶点vi和顶点vj,迭代更新最短路径。Bellman-Ford算法的时间复杂度为O(N^3),而Dijkstra算法的时间复杂度为O(N^2),因此对于不带有负权的图,应当使用Dijkstra求最短路径而非使用Bellman-Ford算法。
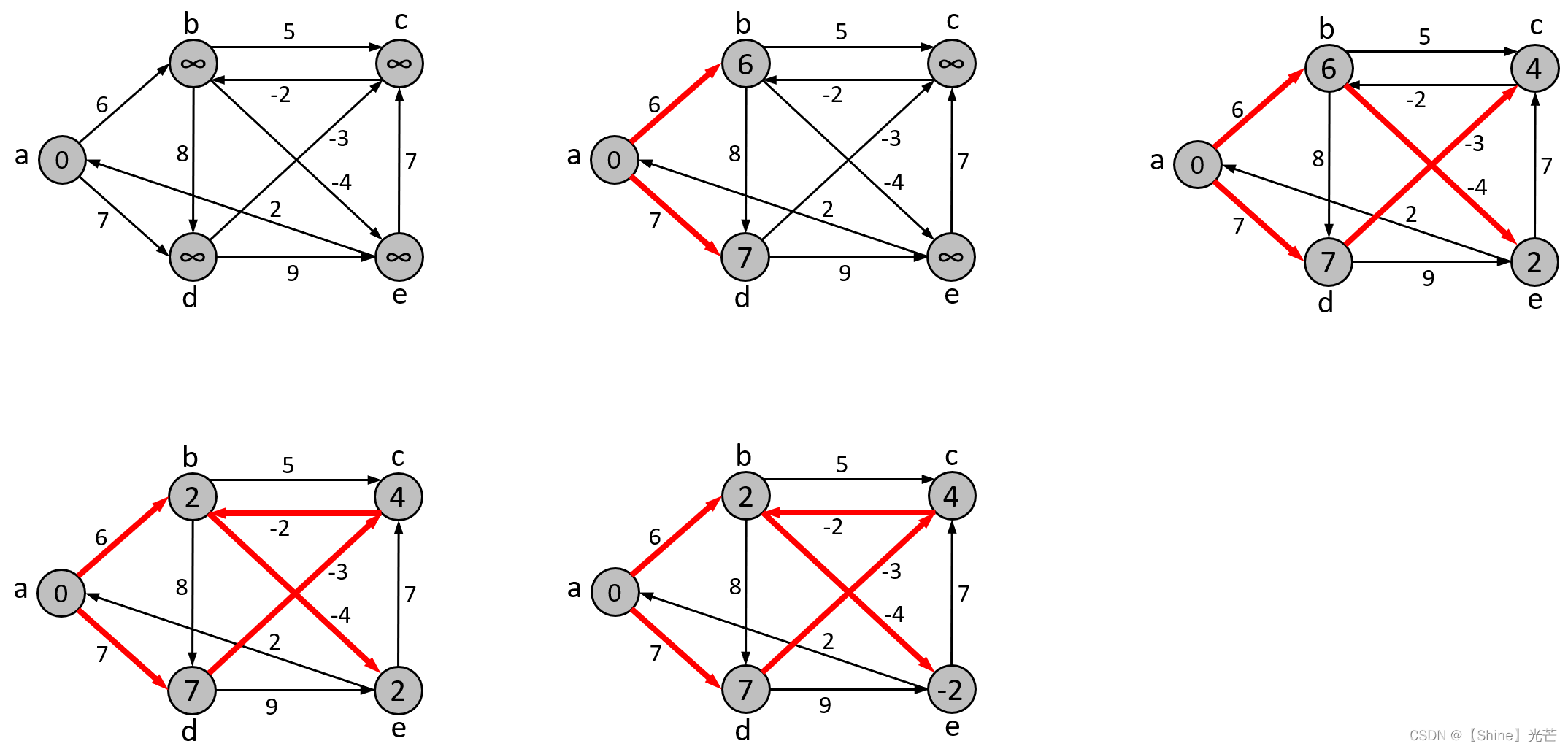
但是,Bellman-Ford算法无法解决负权回路,所谓负权回路,就是图结构中的某个环,其所有边的权值累加起来小于0,就是负权回路。如图5.3所示的图,a->b->d->a就是一个负权回路,a->b->d->a的权值加起来为-2,这样就存在一种诡异的现象,即每一次从a出发再回到a,路径权值之和都会变小,这样理论上a->a的路径可以无限小,对于存在负权回路的图,没有任何办法可以解决其最小路径问题!

代码5.2:Bellman-Ford算法的实现
// BellmanFord 算法获取单源最短路径
bool BellmanFord(const V& src, std::vector<W>& dist, std::vector<size_t>& pPath)
{
// 初始化输出型参数
size_t n = _vertex.size();
dist.resize(n, MAX_W);
pPath.resize(n, -1);
size_t srci = GetIndex(src); // 源顶点对应的下标
dist[srci] = 0; // srci->srci距离为0
pPath[srci] = srci; // 原顶点的前导节点记为其自身
for (size_t k = 0; k < n; ++k)
{
// 遍历节点i和节点j,更新迭代
for (size_t i = 0; i < n; ++i)
{
for (size_t j = 0; j < n; ++j)
{
if (dist[i] != MAX_W && _edges[i][j] != MAX_W &&
dist[i] + _edges[i][j] < dist[j])
{
dist[j] = dist[i] + _edges[i][j];
pPath[j] = i;
}
}
}
}
// 检查是否有负权回路,如果有返回false,否则返回true
for (size_t i = 0; i < n; ++i)
{
for (size_t j = 0; j < n; ++j)
{
if (_edges[i][j] != MAX_W && dist[i] + _edges[i][j] < dist[j])
{
return false;
}
}
}
return true;
}5.3 Floyd-Warshall算法
Floyd-Warshall算法(弗洛伊德算法),是用于计算多源最短路径的算法,其基本原理为三维动态规划算法:
设为,从顶点i到定点j,仅以 {1,2,...,k}顶点为中间顶点的情况下的最短路径和。
- 若i->j的最短路径经过k,那么
- 如i->j的最短路径不经过k,那么
状态转移方程为:
Floyd-Warshall算法的本质是三维动态规划算法,D[i][j][k]表示的是从顶点i到顶点j,在只经过0~k个中间顶点的情况下的最短路径。通过优化将最后一维k优化掉,这是只需要二维数组D[i][j]就可以计算出多源最短路径,Floyd-Warshall算法的时间复杂度为O(N^3),空间复杂度为O(N^2),且Floyd-Warshall算法可以解决带有负权的图的问题。
代码5.3:Floyd-Warshall算法的实现
// FloydWarshall算法计算多源最短路径
void FloydWarshall(std::vector<std::vector<W>>& vvDist, std::vector<std::vector<size_t>>& vvPath)
{
// 初始化记录路径和的数组和记录前导节点的数组
size_t n = _vertex.size();
vvDist.resize(n, std::vector<W>(n, MAX_W));
vvPath.resize(n, std::vector<size_t>(n, -1));
// 将图中直接相连的边添加到vvDist和vvPath中去
for (size_t i = 0; i < n; ++i)
{
for (size_t j = 0; j < n; ++j)
{
if (_edges[i][j] != MAX_W)
{
vvDist[i][j] = _edges[i][j];
vvPath[i][j] = i;
}
if (i == j)
{
vvDist[i][j] = 0;
vvPath[i][j] = i;
}
}
}
// 三维数组动态规划查找多源最短路径
for (size_t k = 0; k < n; ++k)
{
bool change = false;
for (size_t i = 0; i < n; ++i)
{
for (size_t j = 0; j < n; ++j)
{
if (vvDist[i][k] != MAX_W && vvDist[k][j] != MAX_W &&
vvDist[i][k] + vvDist[k][j] < vvDist[i][j])
{
change = true;
vvDist[i][j] = vvDist[i][k] + vvDist[k][j];
vvPath[i][j] = vvPath[k][j];
}
}
}
if (change == false)
{
break;
}
}
}六. 总结
- 图是一种存储顶点和边的数据结构,记为G={V,E},图还可以细分为带权图和无权图、有向图和无向图。
- 图的存储结构有邻接表和邻接矩阵两种格式,这两种方式各有优劣,但对于稠密图,一般使用邻接矩阵。
- 最小生成树是在无向连通图中,能够将每个顶点连接起来的、边权值和最小的子树,通过Kruskal算法和Prim算法可以获取最小生成树,这两种算法的策略都是局部贪心。
- Dijkstra算法和Bellman-Ford算法可以计算单源最短路径问题,Dijkstra算法无法计算带负权的图的最小路径,Bellman-Ford算法可以解决负权问题,但是Dijkstra算法的时间复杂度为O(N^2),Bellman-Ford算法的时间复杂度为O(N^3)。
- Floyd-Warshall算法用于计算多源最短路径问题,这种算法的思想是动态规划,可以解决负权问题,时间复杂度为O(N^3)。
