一、对称性

101. 对称二叉树

101. 对称二叉树

对于二叉树是否对称，要比较的是根节点的左子树与右子树是不是相互翻转的，其实我们要比较的是两个树（这两个树是根节点的左右子树），所以在递归遍历的过程中，也是要同时遍历两棵树。要比较的是两个子树的里侧和外侧的元素是否相等

本题遍历只能是“后序遍历”，因为我们要通过递归函数的返回值来判断两个子树的内侧节点和外侧节点是否相等。

因为要遍历两棵树而且要比较内侧和外侧节点，所以准确的来说是一个树的遍历顺序是左右中，一个树的遍历顺序是右左中。

1.递归

• 递归函数参数为左子树结点和右子树结点，返回值为bool类型

• 节点为空的情况有：

  • 左节点为空，右节点不为空，不对称，return false
  • 左不为空，右为空，不对称 return false
  • 左右都为空，对称，返回true

• 此时已经排除掉了节点为空的情况，那么剩下的就是左右节点不为空：
  左右都不为空，比较节点数值，不相同就return false

• 单层递归的逻辑就是处理 左右节点都不为空，且数值相同的情况。

  • 比较二叉树外侧是否对称：传入的是左节点的左孩子，右节点的右孩子。
  • 比较内测是否对称，传入左节点的右孩子，右节点的左孩子。
  • 如果左右都对称就返回true ，有一侧不对称就返回false 。

class Solution {
    boolean compare(TreeNode left,TreeNode right) {
        if (left==null&&right==null) return true;
        else if (left!=null&&right==null) return false;
        else if (left==null&&right!=null) return false;
        else if (left.val!=right.val) return false;
        // 左右节点都不为空，且数值相同的情况
        // 此时才做递归，做下一层的判断
        boolean outside = compare(left.left,right.right);//外侧比较
        boolean inside = compare(left.right,right.left);//内侧比较
        return outside && inside;
    }
    public boolean isSymmetric(TreeNode root) {
        if (root==null) return true;
        return compare(root.left,root.right);
    }
}

2.迭代

1）使用队列：

这里我们可以使用队列来比较两个树（根节点的左右子树）是否相互翻转，（注意这不是层序遍历）
迭代法，其实是把左右两个子树要比较的元素顺序放进一个容器，然后成对成对的取出来进行比较，那么其实使用栈也是可以的。只要直接把队列改成栈就可以了。

代码随想录动画：

class Solution {
    public boolean isSymmetric(TreeNode root) {
        Queue<TreeNode> deque = new LinkedList<>();
        deque.offer(root.left);
        deque.offer(root.right);
        while (!deque.isEmpty()){
            TreeNode leftNode = deque.poll();
            TreeNode rightNode = deque.poll();
            if (leftNode == null && rightNode == null) {
                continue; //左右结点都为空，对称
            }
            if (leftNode == null && rightNode != null) return false;
            if (leftNode != null && rightNode == null) return false;
            if (leftNode.val != rightNode.val) return false;

            deque.offer(leftNode.left);  // 加入左节点左孩子
            deque.offer(rightNode.right);// 加入右节点右孩子（与左节点左孩子对应比较）
            deque.offer(leftNode.right); // 加入左节点右孩子
            deque.offer(rightNode.left); // 加入右节点左孩子（与左节点右孩子对应比较）
        }
        return true;
    }
}

2）使用双端队列：

也可以使用双端队列，相当于两个栈。这时结点孩子的入队顺序与上面不同

class Solution {
    public boolean isSymmetric(TreeNode root) {
        Deque<TreeNode> deque = new LinkedList<>();
        deque.offerFirst(root.left);
        deque.offerLast(root.right);
        while (!deque.isEmpty()){
            TreeNode leftNode = deque.pollFirst();
            TreeNode rightNode = deque.pollLast();
            if (leftNode == null && rightNode == null) {
                continue; //左右结点都为空，对称
            }
            if (leftNode == null && rightNode != null) return false;
            if (leftNode != null && rightNode == null) return false;
            if (leftNode.val != rightNode.val) return false;

            deque.offerFirst(leftNode.left);  // 先左节点左孩子
            deque.offerFirst(leftNode.right); // 后左节点右孩子
            deque.offerLast(rightNode.right); // 先右节点右孩子
            deque.offerLast(rightNode.left);   // 后右节点左孩子
        }
        return true;
    }
}

3.同类题：

100. 相同的树

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

题解：
如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        return compare(p, q);
    }
    public boolean compare(TreeNode tree1, TreeNode tree2) {
      if(tree1==null && tree2==null)return true;
      if(tree1==null || tree2==null)return false;
      if(tree1.val!=tree2.val)return false;
      // 此时是左右节点都不为空，且数值相同的情况
      // 此时才做递归，做下一层的判断
      boolean compareLeft = compare(tree1.left, tree2.left);       // 左子树：左、 右子树：左
      boolean compareRight = compare(tree1.right, tree2.right);    // 左子树：右、 右子树：右
      boolean isSame = compareLeft && compareRight;                  // 左子树：中、 右子树：中
      return isSame;
  }
}

572. 另一棵树的子树

给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。

二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

题解：
要判断一个树subRoot是不是树root的子树，那么可以判断subRoot是否和树root的任意子树相等。即，在root的每个子节点上，判断该子节点是否和subRoot相等。
subRoot是root的左子树或subRoot是root的右子树或subRoot与root相同就说明root中包含和subRoot具有相同结构和节点值的子树。

class Solution {
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        if (subRoot==null) return true;
        if (root==null) return false;
        boolean left = isSubtree(root.left,subRoot);  //subRoot是否是root的左子树
        boolean right = isSubtree(root.right,subRoot);//subRoot是否是root的右子树
        boolean equal = compare(root,subRoot);        //subRoot是否与root相同
        return left||right||equal;  //或关系
    }
    //判断是同一颗树
    public boolean compare(TreeNode tree1, TreeNode tree2) {
      if(tree1==null && tree2==null)return true;
      if(tree1==null || tree2==null)return false;
      if(tree1.val!=tree2.val)return false;              
      return compare(tree1.left, tree2.left)&&compare(tree1.right, tree2.right);
  }
}

PS：本题还可用串匹配或树哈希优化。

二、深度

104. 二叉树的最大深度

104. 二叉树的最大深度

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例： 给定二叉树 [3,9,20,null,null,15,7]，

返回它的最大深度 3 。

1.递归

本题可以使用前序（中左右），也可以使用后序遍历（左右中），使用前序求的就是深度，使用后序求的是高度。而根节点的高度就是二叉树的最大深度

• 递归函数的参数和返回值：参数就是传入树的根节点，返回就返回这棵树的深度，所以返回值为int类型。
• 终止条件：如果为空节点的话，就返回0，表示高度为0。
• 单层递归的逻辑：先求它的左子树的深度，再求的右子树的深度，最后取左右深度最大的数值 再+1 （加1是因为算上当前中间节点）就是目前节点为根节点的树的深度。

1）后序

class Solution {
    public int maxDepth(TreeNode root) {
        if (root==null) return 0;
        int leftdepth = maxDepth(root.left);       // 左
        int rightdepth = maxDepth(root.right);     // 右
        int depth = 1 + Math.max(leftdepth, rightdepth); // 中
        return depth;
    }
}

1）前序

使用了前序（中左右）的遍历顺序，这才是真正求深度的逻辑

class Solution {
    int result;
    void getdepth(TreeNode node, int depth) {
        result = depth > result ? depth : result; // 中

        if (node.left == null && node.right == null) return ;

        if (node.left!=null) { // 左
            depth++;    // 深度+1
            getdepth(node.left, depth);
            depth--;    // 回溯，深度-1
        }
        if (node.right!=null) { // 右
            depth++;    // 深度+1
            getdepth(node.right, depth);
            depth--;    // 回溯，深度-1
        }
//	   上面表现出了深度回溯过程，可以简化为以下:
//        if (node.left) { 
//            getdepth(node/left, depth + 1);
//        }
//        if (node.right) { 
//            getdepth(node.right, depth + 1);
//        }
        return ;
    }
    public int maxDepth(TreeNode root) {
        result = 0;
        if (root==null) return 0;
        getdepth(root, 1);
        return result;
    }
}

2.迭代（层序）

迭代法使用层序遍历是最为合适的，因为最大的深度就是二叉树的层数，和层序遍历的方式极其吻合。

在二叉树中，一层一层的来遍历二叉树，记录一下遍历的层数就是二叉树的深度

class Solution {
    public int maxDepth(TreeNode root) {
        if (root==null) return 0;
        Deque<TreeNode> deque = new LinkedList<>();
        deque.offer(root);
        int depth = 0;
        while (!deque.isEmpty()) {
            int size = deque.size();
            depth++;
            for (int i = 0; i < size; i++) {
                TreeNode poll = deque.poll();
                if (poll.left != null) {
                    deque.offer(poll.left);
                }
                if (poll.right != null) {
                    deque.offer(poll.right);
                }
            }
        }
        return depth;
    }
}

559. N 叉树的最大深度

559. N 叉树的最大深度

给定一个 N 叉树，找到其最大深度。

最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。

N 叉树输入按层序遍历序列化表示，每组子节点由空值分隔

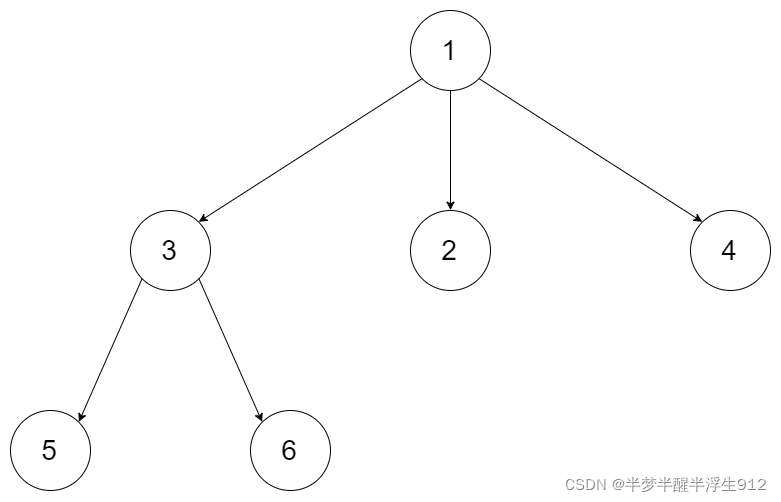
输入：root = [1,null,3,2,4,null,5,6]
输出：3

1.递归（深度优先）

时间复杂度：$O(n)$
空间复杂度：$O(hight)$

class Solution {
    public int maxDepth(Node root) {
        if (root==null) return 0;
        int depth = 0;
        if (root.children!=null) {
            for (Node child : root.children) {
                depth = Math.max(depth,maxDepth(child));
            }
        }
        return depth+1;
    }
}

2.迭代（广度优先）

时间复杂度：$O(n)$
空间复杂度：$O(n)$

class Solution {
    public int maxDepth(Node root) {
        if (root==null) return 0;
        int depth = 0;
        Queue<Node> que = new LinkedList<>();
        que.offer(root);
        while (!que.isEmpty())
        {
            depth++;
            int len = que.size();
            while (len > 0)
            {
                Node node = que.poll();
                for (int i = 0; i < node.children.size(); i++)
                    if (node.children.get(i) != null) 
                        que.offer(node.children.get(i));
                len--;
            }
        }
        return depth;
    }
}

111. 二叉树的最小深度

111. 二叉树的最小深度

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明: 叶子节点是指没有子节点的节点。

示例:

给定二叉树 [3,9,20,null,null,15,7],

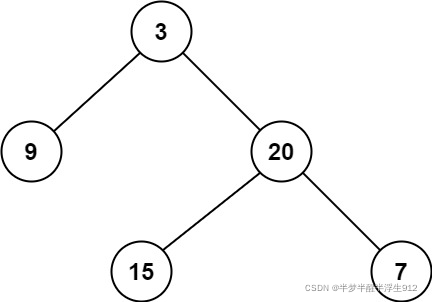
返回它的最小深度 2.

时间复杂度：$O(n)$
空间复杂度：$O(n)$

1.递归

使用后序遍历，因为要比较递归返回之后的结果

• 递归函数的参数和返回值：参数为要传入的二叉树根节点，返回的是int类型的深度。
• 终止条件：也是遇到空节点返回0，表示当前节点的高度为0。
• 单层递归的逻辑：如果左子树为空，右子树不为空，说明最小深度是 1 + 右子树的深度。
  反之，右子树为空，左子树不为空，最小深度是 1 + 左子树的深度。
  最后，如果左右子树都不为空，返回左右子树深度最小值 + 1 。

class Solution {
    public int minDepth(TreeNode root) {
        if (root==null) return 0;
        int leftDepth = minDepth(root.left);   //左
        int rightDepth = minDepth(root.right); //右
                                               //中
        // 当一个左子树为空，右不为空，这时并不是最低点
        if (root.left==null) return rightDepth+1;
        // 当一个右子树为空，左不为空，这时并不是最低点
        if (root.right==null) return leftDepth+1;
        // 左右结点都不为空
        return Math.min(leftDepth,rightDepth)+1;
    }
}

2.迭代

使用层序遍历

只有当左右孩子都为空的时候，才说明遍历的最低点了。如果其中一个孩子为空则不是最低点

class Solution {
    public int minDepth(TreeNode root) {
        if (root==null) return 0;
        int depth = 0;
        Deque<TreeNode> deque = new LinkedList<>();
        deque.offer(root);
        while (!deque.isEmpty()) {
            int size = deque.size();
            depth++; // 记录最小深度
            for (int i = 0; i < size; i++) {
                TreeNode node = deque.poll();
                if (node.left == null && node.right == null) {
                    // 是叶子结点，直接返回depth，从上往下遍历，所以该值就是最小值
                    return depth;
                }
                if (node.left != null) deque.offer(node.left);
                if (node.right != null) deque.offer(node.right);
            }
        }
        return depth;
    }
}

三、高度

110. 平衡二叉树

110. 平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。

示例 1:

给定二叉树 [3,9,20,null,null,15,7]

返回 true 。

PS：关于根节点的深度究竟是1 还是 0，不同的地方有不一样的标准，leetcode的题目中都是以节点为一度，即根节点深度是1。但维基百科上定义用边为一度，即根节点的深度是0

因为求深度可以从上到下去查，所以需要前序遍历（中左右），而高度只能从下到上去查，所以只能后序遍历（左右中）

1.递归

• 参数和返回值：参数：当前传入节点。返回值：以当前传入节点为根节点的树的高度。
• 终止条件：遇到空节点了为终止，返回0，表示当前节点为根节点的树高度为0
• 单层递归的逻辑：分别求出其左右子树的高度，然后如果差值小于等于1，则返回当前二叉树的高度，否则则返回-1，表示已经不是二叉平衡树了。

时间复杂度：$O(n)$
空间复杂度：$O(n)$

class Solution {
    public boolean isBalanced(TreeNode root) {
        return getHeight(root) != -1;
    }
    int getHeight(TreeNode root) {
        if (root == null) return 0;
        int leftHeight = getHeight(root.left);
        if (leftHeight == -1) return -1;
        int rightHeight = getHeight(root.right);
        if (rightHeight == -1) return -1;
        // 左右子树高度差大于1，return -1表示已经不是平衡树了
        if (Math.abs(leftHeight - rightHeight) > 1) {
            return -1;
        }
        return Math.max(leftHeight, rightHeight) + 1;
    }
}

2.迭代

可以先定义一个函数，专门用来求高度。这个函数通过栈模拟的后序遍历找每一个节点的高度（其实是通过求传入节点为根节点的最大深度来求的高度）然后再用栈来模拟前序遍历，遍历每一个节点的时候，再去判断左右孩子的高度是否符合
此题迭代效率较低，计算高度时会重复遍历
时间复杂度：$O(n^2)$

四、结点

222. 完全二叉树的节点个数

222. 完全二叉树的节点个数

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例 1：

输入：root = [1,2,3,4,5,6]
输出：6
示例 2：

输入：root = []
输出：0
示例 3：

输入：root = [1]
输出：1
提示：

树中节点的数目范围是[0, 5 * 10^4]
0 <= Node.val <= 5 * 10^4
题目数据保证输入的树是 完全二叉树

1.对普通二叉树的求法

1）递归

先求它的左子树的节点数量，再求的右子树的节点数量，最后取总和再加一 （加1是因为算上当前中间节点）就是目前节点为根节点的节点数量。

时间复杂度：$O(n)$
空间复杂度：$O(\log n)$

class Solution {
    public int countNodes(TreeNode root) {
        if(root == null) return 0;
        return countNodes(root.left) + countNodes(root.right) + 1;
    }
}

2）迭代

加一个变量result，统计节点数量

时间复杂度：$O(n)$
空间复杂度：$O(n)$

class Solution {
    public int countNodes(TreeNode root) {
        if (root == null) return 0;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int result = 0;
        while (!queue.isEmpty()) {
            int size = queue.size();
            while (size -- > 0) {
                TreeNode cur = queue.poll();
                result++; // 记录节点数量
                if (cur.left != null) queue.offer(cur.left);
                if (cur.right != null) queue.offer(cur.right);
            }
        }
        return result;
    }
}

2.对完全二叉树的求法

完全二叉树只有两种情况，情况一：就是满二叉树，情况二：最后一层叶子节点没有满。

对于情况一，可以直接用 2^树深度 - 1 来计算，注意这里根节点深度为1。

对于情况二，分别递归左孩子，和右孩子，递归到某一深度一定会有左孩子或者右孩子为满二叉树，然后依然可以按照情况1来计算。

时间复杂度：$O(\log n\times \log n)$
空间复杂度：$O(\log n)$

class Solution {
    public int countNodes(TreeNode root) {
        if (root == null) return 0;
        int leftDepth = getDepth(root.left);// 求左子树深度
        int rightDepth = getDepth(root.right);// 求右子树深度
        if (leftDepth == rightDepth) {// 左子树是满二叉树
            // 2^leftDepth其实是 （2^leftDepth - 1） + 1 ，左子树 + 根结点
            return (1 << leftDepth) + countNodes(root.right);
        } else {// 右子树是满二叉树
            return (1 << rightDepth) + countNodes(root.left);
        }
    }
    int getDepth(TreeNode root) {
        int depth = 0;
        while (root != null) {
            root = root.left;
            depth++;
        }
        return depth;
    }
}

五、路径

543. 二叉树的直径

543. 二叉树的直径
给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。

示例 :
给定二叉树

      1
     / \
    2   3
   / \     
  4   5    

返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。

思路

每一条二叉树的「直径」长度，就是一个节点的左右子树的最大深度之和。
求整棵树中的最长「直径」，那直接思路就是遍历整棵树中的每个节点，然后通过每个节点的左右子树的最大深度算出每个节点的「直径」，最后把所有「直径」求个最大值即可。

应该把计算「直径」的逻辑放在后序位置，后序位置可得到左右子树的最大深度。

时间复杂度：$O(n)$
空间复杂度：$O(hight)$

class Solution {
    int maxDiameter = 0;
    public int diameterOfBinaryTree(TreeNode root) {
        maxDepth(root);
        return maxDiameter;
    }
    //求最大深度
    int maxDepth(TreeNode root) {
    if (root == null) return 0;
    int leftMax = maxDepth(root.left);
    int rightMax = maxDepth(root.right);
    //后序位置计算直径
    int myDiameter = leftMax + rightMax;
    maxDiameter = Math.max(maxDiameter, myDiameter);

    return 1 + Math.max(leftMax, rightMax);
    }
}

257. 二叉树的所有路径

257. 二叉树的所有路径

给定一个二叉树，返回所有从根节点到叶子节点的路径。

说明: 叶子节点是指没有子节点的节点。

示例:

1.递归

要求从根节点到叶子的路径，所以需要前序遍历，这样才方便让父节点指向孩子节点，找到对应的路径。要把路径记录下来，需要回溯来回退一个路径进入另一个路径。

• 函数函数参数以及返回值：要传入根节点，记录每一条路径的path，和存放结果集的result，这里递归不需要返回值。用List记录路径，方便下面的回溯
• 递归终止条件：当 cur不为空，其左右孩子都为空的时候，就找到叶子节点，开始结束的处理逻辑。
• 单层递归逻辑：因为是前序遍历，需要先处理中间节点，中间节点就是我们要记录路径上的节点，先放进path中。然后是递归和回溯的过程，上面没有判断cur是否为空，那么在这里递归的时候，如果为空就不进行下一层递归。

class Solution {
    public List<String> binaryTreePaths(TreeNode root) {
        List<String> res = new ArrayList<>();
        if (root == null) return res;
        List<Integer> paths = new ArrayList<>();
        traversal(root, paths, res);
        return res;
    }
    void traversal(TreeNode root, List<Integer> paths, List<String> res) {
        paths.add(root.val);
        // 叶子结点
        if (root.left == null && root.right == null) {
            // 输出
            StringBuilder sb = new StringBuilder();
            for (int i = 0; i < paths.size() - 1; i++) {
                sb.append(paths.get(i)).append("->");
            }
            sb.append(paths.get(paths.size() - 1));
            res.add(sb.toString());
            return;
        }
        if (root.left != null) {
            traversal(root.left, paths, res);
            paths.remove(paths.size() - 1);// 回溯
        }
        if (root.right != null) {
            traversal(root.right, paths, res);
            paths.remove(paths.size() - 1);// 回溯
        }
    }
}

2.迭代

使用前序遍历的迭代方式来模拟遍历路径的过程，可以直接定义一个成员变量为object的栈，同时模拟递归和存放遍历路径。

class Solution {
    public List<String> binaryTreePaths(TreeNode root) {
        List<String> result = new ArrayList<>();
        if (root == null)
            return result;
        Stack<Object> stack = new Stack<>();
        // 节点和路径同时入栈
        stack.push(root);
        stack.push(root.val + "");
        while (!stack.isEmpty()) {
            // 节点和路径同时出栈
            String path = (String) stack.pop();
            TreeNode node = (TreeNode) stack.pop();
            // 若找到叶子节点
            if (node.left == null && node.right == null) {
                result.add(path);
            }
            //右子节点不为空
            if (node.right != null) {
                stack.push(node.right);
                stack.push(path + "->" + node.right.val);
            }
            //左子节点不为空
            if (node.left != null) {
                stack.push(node.left);
                stack.push(path + "->" + node.left.val);
            }
        }
        return result;
    }
}

112. 路径总和

112. 路径总和

给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。

说明: 叶子节点是指没有子节点的节点。

示例: 给定如下二叉树，以及目标和 sum = 22，

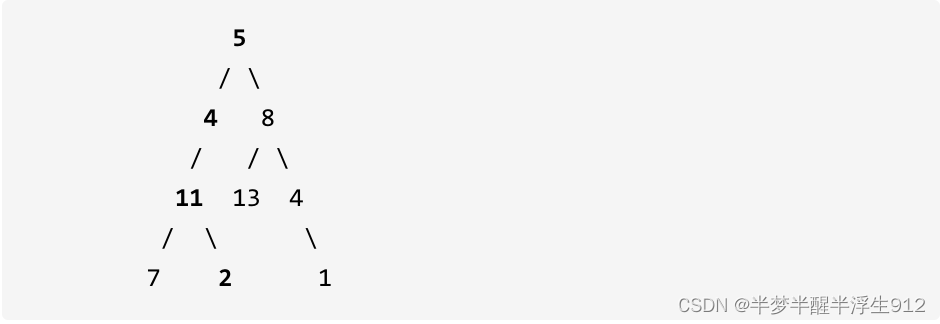
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。

1.递归

可以使用深度优先遍历的方式（本题前中后序都可以，无所谓，因为中节点也没有处理逻辑）来遍历二叉树

• 递归函数的参数和返回类型：参数需要二叉树的根节点，还需要一个计数器用来计算二叉树的一条边之和是否正好是目标和，计数器为int型。要找一条符合条件的路径，所以递归函数需要返回值，及时返回。返回值可用布尔类型表示，路径总和等于目标值就返回true。
• 终止条件：累加然后判断是否等于目标和，代码比较麻烦，可以用递减，让计数器count初始为目标和，然后每次减去遍历路径节点上的数值。
  如果最后count == 0，同时到了叶子节点的话，说明找到了目标和。
  如果遍历到了叶子节点，count不为0，就是没找到。
• 单层递归的逻辑：终止条件是判断叶子节点，所以递归的过程中就不要让空节点进入递归了。
  递归函数是有返回值的，如果递归函数返回true，说明找到了合适的路径，应该立刻返回。

class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if (root==null) return false;
        targetSum -= root.val;
        //叶子节点
        if (root.left==null&&root.right==null)
            return targetSum==0;//计数是为0，则存在路径
        if (root.left != null) {
            boolean left = hasPathSum(root.left, targetSum);
            if (left) return true; // 已经找到
        }
        if (root.right != null) {
            boolean right = hasPathSum(root.right,targetSum);
            if (right) return true;
        }
        return false;
    }
}

递归简化：

class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if (root == null) return false; // 为空退出
        // 叶子节点判断是否符合
        if (root.left == null && root.right == null) return root.val == targetSum;
        // 求两侧分支的路径和
        return hasPathSum(root.left, targetSum - root.val) || hasPathSum(root.right, targetSum - root.val);
    }
}

递归函数什么时候需要返回值？什么时候不需要返回值？

如果需要搜索整棵二叉树且不用处理递归返回值，递归函数就不要返回值。（113.路径总和ii）
如果需要搜索整棵二叉树且需要处理递归返回值，递归函数就需要返回值。 （236. 二叉树的最近公共祖先）
如果要搜索其中一条符合条件的路径，那么递归一定需要返回值，因为遇到符合条件的路径了就要及时返回。（本题112. 路径总和）

2.迭代

栈里一个元素不仅要记录该节点指针，还要记录从头结点到该节点的路径数值总和。可以使用两个栈分别记录。相对复杂一些。

class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if(root==null) return false;
        Stack<TreeNode> stack1 = new Stack<>();
        Stack<Integer> stack2 = new Stack<>();
        stack1.push(root); stack2.push(root.val);
        while(!stack1.isEmpty()){
            int size = stack1.size();
            for(int i=0;i<size;i++){
                TreeNode node = stack1.pop(); int sum=stack2.pop();
                // 如果该节点是叶子节点了，同时该节点的路径数值等于sum，那么就返回true
                if(node.left==null && node.right==null && sum==targetSum) return true;
                // 右节点，压进去一个节点的时候，将该节点的路径数值也记录下来
                if(node.right!=null){
                    stack1.push(node.right); stack2.push(sum+node.right.val);
                }
                // 左节点，压进去一个节点的时候，将该节点的路径数值也记录下来
                if(node.left!=null){
                    stack1.push(node.left); stack2.push(sum+node.left.val);
                }
            }
        }
        return false;
    }
}

113. 路径总和 II

113. 路径总和 II

给定一个二叉树和一个目标和，找到所有从根节点到叶子节点路径总和等于给定目标和的路径。

说明: 叶子节点是指没有子节点的节点。

示例: 给定如下二叉树，以及目标和 sum = 22，

递归

要遍历整个树，找到所有路径，所以递归函数不要返回值

法1：

class Solution {
    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        List<List<Integer>> res = new ArrayList<>();
        if (root == null) return res; // 非空判断
        
        List<Integer> path = new LinkedList<>();
        preorderdfs(root, targetSum, res, path);
        return res;
    }
    void preorderdfs(TreeNode root,int targetSum,List<List<Integer>> res,List<Integer> path) {
        path.add(root.val);
        // 遇到了叶子节点
        if (root.left == null && root.right == null) {
            // 找到了和为 targetSum 的路径
            if (targetSum - root.val == 0) {
                res.add(new ArrayList<>(path));
            }
            return; // 如果和不为 targetSum，返回
        }

        if (root.left != null) {
            preorderdfs(root.left, targetSum - root.val, res, path);
            path.remove(path.size() - 1); // 回溯
        }
        if (root.right != null) {
            preorderdfs(root.right, targetSum - root.val, res, path);
            path.remove(path.size() - 1); // 回溯
        }
    }
}

法2：

class Solution {
    List<List<Integer>> result;
    LinkedList<Integer> path;
    public List<List<Integer>> pathSum (TreeNode root,int targetSum) {
        result = new LinkedList<>();
        path = new LinkedList<>();
        travesal(root, targetSum);
        return result;
    }
    void travesal(TreeNode root,  int count) {
        if (root == null) return;
        path.offer(root.val);
        count -= root.val;
        if (root.left == null && root.right == null && count == 0) {
            result.add(new LinkedList<>(path));
        }
        travesal(root.left, count);
        travesal(root.right, count);
        path.removeLast(); // 回溯
    }
}

六、求值

404. 左叶子之和

404. 左叶子之和

计算给定二叉树的所有左叶子之和。

示例：

注意：
如果一个节点的左节点不为空，且左节点没有左右孩子，那么这个节点的左节点就是左叶子。判断当前节点是不是左叶子是无法判断的，必须要通过节点的父节点来判断其左孩子是不是左叶子。

1.递归

递归的遍历顺序为后序遍历（左右中），是因为要通过递归函数的返回值来累加求取左叶子数值之和。

• 递归函数的参数和返回值：要传入树的根节点，递归函数的返回值为数值之和，所以为int
• 终止条件：root == NULL
• 单层递归的逻辑：判断当遇到左叶子节点的时候，记录数值，然后通过递归求取左子树左叶子之和，和 右子树左叶子之和，相加便是整个树的左叶子之和。

时间复杂度：$O(n)$
空间复杂度：$O(n)$

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        if (root == null) return 0;
        int leftValue = sumOfLeftLeaves(root.left);    // 左
        int rightValue = sumOfLeftLeaves(root.right);  // 右
                                                       
        int midValue = 0;
        if (root.left != null && root.left.left == null && root.left.right == null) { 
            midValue = root.left.val;
        }
        int sum = midValue + leftValue + rightValue;  // 中
        return sum;
    }
}

2.迭代

前中后序和层序遍历都可

时间复杂度：$O(n)$
空间复杂度：$O(n)$
迭代前序：

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        if (root == null) return 0;
        Stack<TreeNode> stack = new Stack<> ();
        stack.add(root);
        int result = 0;
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            if (node.left != null && node.left.left == null && node.left.right == null) {
                result += node.left.val;
            }
            if (node.right != null) stack.add(node.right);
            if (node.left != null) stack.add(node.left);
        }
        return result;
    }
}

迭代层序：

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        int sum = 0;
        if (root == null) return 0;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            int size = queue.size();
            while (size -- > 0) {
                TreeNode node = queue.poll();
                if (node.left != null) { // 左节点不为空
                    queue.offer(node.left);
                    if (node.left.left == null && node.left.right == null){ // 左叶子节点
                        sum += node.left.val;
                    }
                }
                if (node.right != null) queue.offer(node.right);
            }
        }
        return sum;
    }
}

513. 找树左下角的值

513. 找树左下角的值

给定一个二叉树，在树的最后一行找到最左边的值。

示例 1:

1.递归

深度最大的叶子节点一定是最后一行，所以要找深度最大的叶子节点。找最左边的可以使用前序遍历，这样优先在左边搜索，然后记录深度最大的叶子节点，此时就是树的最后一行最左边的值。

• 参数和返回值：参数有要遍历树的根节点，还有一个int型的变量用来记录最大深度。 不需要返回值。（如果需要遍历整棵树，递归函数就不能有返回值。如果需要遍历某一条固定路线，递归函数就一定要有返回值！）
  本题还需要类里的两个全局变量，maxLen用来记录最大深度，maxleftValue记录最大深度最左节点的数值。
• 终止条件：遇到叶子节点就更新最大深度
• 单层递归逻辑：求最大深度，递归的过程中依然要使用回溯

class Solution {
    int maxLen = 0;
    int maxleftValue;
    public int findBottomLeftValue(TreeNode root) {
        maxleftValue = root.val;
        findLeftValue(root,0);
        return maxleftValue;
    }

    void findLeftValue(TreeNode root,int deep) {
        if (root==null) return;
        if (root.left==null && root.right==null) {
            if (deep>maxLen) {
                maxleftValue = root.val;
                maxLen = deep;
            }
        }
        //隐藏回溯
        if (root.left != null) findLeftValue(root.left,deep + 1);
        if (root.right != null) findLeftValue(root.right,deep + 1);
    }
}

2.迭代

本题更适合使用层序遍历，只需要记录最后一行第一个节点的数值就可以了。

class Solution {
    public int findBottomLeftValue(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int res = 0;
        while (!queue.isEmpty()) {
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                TreeNode poll = queue.poll();
                if (i == 0) //每层最左端
                    res = poll.val;
                if (poll.left != null) 
                    queue.offer(poll.left);
                if (poll.right != null) 
                    queue.offer(poll.right);
            }
        }
        return res;
    }
}