LeetCode105.从前序和中序遍历序列构造二叉树

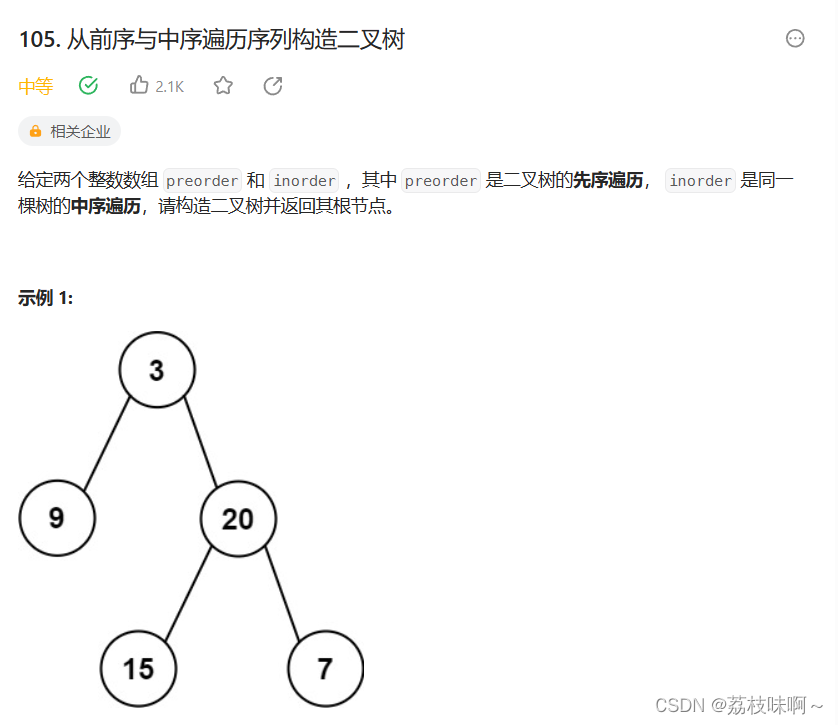
 这道题看完题想了几分钟就想到大概的思路了，但是在写的时候有很多细节没注意出了很多问题，然后写了1个多小时，其实这道题挺简单的。

首先，最基本的知识，先序遍历是根左右，中序遍历是左根右，那么我们一眼可以知道：根节点是先序遍历的第一个节点，然后又可以在中序遍历中找到这个根节点(树中每个val都不相等)，中序遍历中根节点的左变是左子树，根节点的右遍是右子树。

那么这个题目应该怎么解呢？首先，对于树的题目要么递归要么用队列或栈，我选择用递归。根据上面发现的几个点，我想到了递归函数：

public TreeNode dfs(int[] preorder, int[] inorder)

通过这两个遍历序列我们可以创建出根节点，然后我们在从preorder和inorder中找出来左子树的leftPreorder和leftInorder以及右子树的rightPreorder和rightInorder,然后利用递归

root.left=dfs(leftPreorder, leftInorder);
root.right = dfs(rightPreorder, rightInorder);

大体上的思路就是这样，那么我们如何找出左右子树的前序和中序的遍历序列呢？

首先中序遍历是非常简单的，中序遍历是左根右的顺序，它对于每颗树都是根左右的顺序，所以‘左’就是左子树的中序遍历结果，所以我们在inorder中根节点左边就是leftInorder,根节点右边就是rightInorder。

前序遍历也不难，前序遍历是根左右，preorder第0个数是根节点，后面是左和右，而我们在中序遍历中已经知道了左子树的长度leftLength和右子树的长度rightLength，所有从第1个数往后数leftLength就是左子树的前序遍历leftPreorder，剩下的就是右子树的前序遍历rightPreorder。

然后需要注意的就是，递归的结束，如果左子树的长度小于0就不用递归的创建左子树了，右子树同理，最后返回root。以下是我的代码：

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if(preorder.length == 0){
            return null;
        }else{
            return dfs(preorder, inorder);
        }
    }
    public TreeNode dfs(int[] preorder, int[] inorder){
    TreeNode root = new TreeNode(preorder[0]);

    int leftInorderIndex = 0;
    int rightInorderIndex = 0;
    int leftPreorderIndex = 0;
    int rightPreorderIndex = 0;
    //在中序遍历中找到根节点
    for(int i=0;i<inorder.length;i++){
        if(inorder[i] == root.val){
            leftInorderIndex = i-1;
            rightInorderIndex = i+1;
            break;
        }
    }
    //找到左子树长度和右子树长度
    int leftLength = leftInorderIndex+1;
    int rightLength = inorder.length - rightInorderIndex;

    if(leftLength > 0){
        //创建leftInorder
        int[] leftInorder = new int[leftLength];
        for(int i=0;i<leftInorder.length;i++){
            leftInorder[i] = inorder[i];
        }
        //创建leftPreorder
        int[] leftPreorder = new int[leftLength];
        int index =1;
        for(int i=0;i<leftPreorder.length;i++){
          leftPreorder[i] = preorder[index];
          index++;
        }
        //递归出根节点的左子树
      root.left = dfs(leftPreorder, leftInorder);
        
    }
   
    if(rightLength > 0){
        //创建出rightInorder
        rightPreorderIndex = leftLength+1;
        int[] rightInorder = new int[rightLength];
        int index0= rightInorderIndex;
        for(int i=0;i<rightInorder.length;i++){
           rightInorder[i] = inorder[index0];
           index0++;
        }
        //创建出rightPreorder
        int[] rightPreorder = new int[rightLength];
       int index1 = rightPreorderIndex;
       for(int i=0;i<rightPreorder.length;i++){
          rightPreorder[i] = preorder[index1];
          index1++;
      }
      //递归出根节点的右子树
       root.right = dfs(rightPreorder, rightInorder);
    }
    return root;
    }
}

看看官方题解做法：

题解的方法一用的也是递归，但是他用了一个HashMap来快速定位根节点，还有就是他没有去创建左右子树的前中遍历序列数组，他直接传前序，中序遍历在inorder中的起始下标和终止下标，因为他们在数组中是连续的，这样全局只需要用这个最大的inorder和preorder就可以，不用花费时间和空间去创建数组，以下是题解方法一代码：

class Solution {
    private Map<Integer, Integer> indexMap;

    public TreeNode myBuildTree(int[] preorder, int[] inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {
        if (preorder_left > preorder_right) {
            return null;
        }

        // 前序遍历中的第一个节点就是根节点
        int preorder_root = preorder_left;
        // 在中序遍历中定位根节点
        int inorder_root = indexMap.get(preorder[preorder_root]);
        
        // 先把根节点建立出来
        TreeNode root = new TreeNode(preorder[preorder_root]);
        // 得到左子树中的节点数目
        int size_left_subtree = inorder_root - inorder_left;
        // 递归地构造左子树，并连接到根节点
        // 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
        root.left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1);
        // 递归地构造右子树，并连接到根节点
        // 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
        root.right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right);
        return root;
    }

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        int n = preorder.length;
        // 构造哈希映射，帮助我们快速定位根节点
        indexMap = new HashMap<Integer, Integer>();
        for (int i = 0; i < n; i++) {
            indexMap.put(inorder[i], i);
        }
        return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);
    }
}

题解的第二种方法是迭代，

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if (preorder == null || preorder.length == 0) {
            return null;
        }
        TreeNode root = new TreeNode(preorder[0]);
        Deque<TreeNode> stack = new LinkedList<TreeNode>();
        stack.push(root);
        int inorderIndex = 0;
        for (int i = 1; i < preorder.length; i++) {
            int preorderVal = preorder[i];
            TreeNode node = stack.peek();
            if (node.val != inorder[inorderIndex]) {
                node.left = new TreeNode(preorderVal);
                stack.push(node.left);
            } else {
                while (!stack.isEmpty() && stack.peek().val == inorder[inorderIndex]) {
                    node = stack.pop();
                    inorderIndex++;
                }
                node.right = new TreeNode(preorderVal);
                stack.push(node.right);
            }
        }
        return root;
    }
}