今天学习单调栈解决最后一道题

84.柱状图中的最大矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

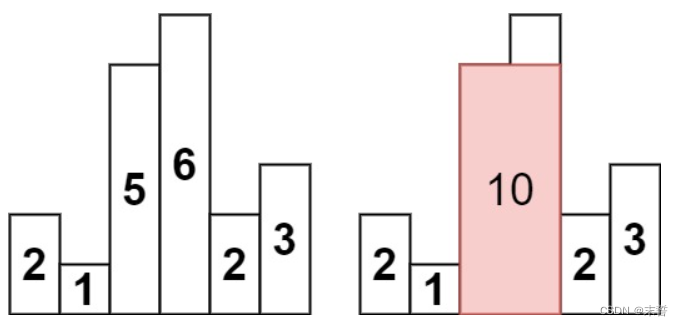
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

思路：

1.本题初见感觉是类似于Day63的接雨水，但单调栈的思路需要稍微转换一下。

2.相比起前面所有题单调栈是从栈顶到栈尾递增，本题是需要栈顶到栈尾递减才行。至于为什么这么做，相当于我们确定一个矩形的高度作为基准，然后来看他的宽度能延伸到何处（相当于找到左边和右边第一个比自己低的高度，此时就无法继续延伸），进而确定算面积的宽度。

3.但本题还需要考虑一种情况，我们如果完全按照接雨水那道题的步骤去做，会发现当原数组是单调递增或是单调递减时就会出现问题：（1）如果原数组是单调递增，因为我们单调栈是栈顶到栈尾递减，因此此时会一直入栈元素直到遍历完整个数组但却没有进行一次面积计算（因为只有当前元素小于栈顶元素时我们实际上才算找到了一次计算的机会）；（2）如果原数组是单调递减，主要涉及到遍历的最初。我们会先将第一个元素压入栈然后从第二个元素开始遍历，但第二个元素比第一个元素小，我们显然需要进行一次计算：以第一个元素为基准，第二个元素是其右边第一个更低的高度，但此时无法找到其左边第一个比自己低的高度。

因此为了解决原数组单调的问题，我们在数组首尾各加入一个0，首部加入0解决单调递减时无法找到第一个元素左边第一个比自己低的高度；尾部加入0解决单调递增时不会进行任何一次计算。

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int result = 0;
        stack<int> st;
        //在原数组首尾插入一个0防止数组纯单调导致发生问题
        heights.insert(heights.begin(), 0);
        heights.push_back(0);
        st.push(0);

        for(int i = 1; i < heights.size(); i++){
            if(heights[i] > heights[st.top()]){
                st.push(i);
            }
            else if(heights[i] == heights[st.top()]){
                st.pop();
                st.push(i);
            }
            else{
                while(!st.empty() && heights[i] < heights[st.top()]){
                    int mid = st.top();
                    st.pop();
                    if(!st.empty()){
                        int left = st.top();
                        int right = i;
                        int w = right - left - 1;
                        int h = heights[mid];
                        result = max(result, w * h);
                    }
                }
                st.push(i);
            }
        }

        return result;
    }
};

启发：

1.对于单调栈这一自己完全不熟系的领域，尽管有了前面一些题的基础，套代码的模板是能套了，但要自己捋清楚思路还是有些困难，在接下来一段时间仍需要继续理解。

2.本题用到了两种变化时定一种的思路，这一思路在之前贪心算法中避免同时考虑两种情况导致顾此失彼时有类似的情况，也相当于是进行了一次复习。

最后的最后，感谢代码随想录总结出来的这一套算法试题，经历了两个月的时间终于全部过完了第一遍，尽管还有不少思想方法自己掌握的不算牢固，但相比起之前几乎零基础的自己也已经提升了不少，也巩固了自己许多基础知识，在以后还会进一步对自己薄弱的环节进行重刷和进一步的集中做题来巩固。完结撒花！