当前位置：首页 > article >正文

SALib敏感性分析入门实践笔记

article 2024/11/20 13:21:11

1. 敏感性分析

敏感性分析是指从定量分析的角度研究有关因素发生某种变化对某一个或一组关键指标影响程度的一种不确定分析技术。其实质是通过逐一改变相关变量数值的方法来解释关键指标受这些因素变动影响大小的规律。敏感性因素一般可选择主要参数（如销售收入、经营成本、生产能力、初始投资、寿命期、建设期、达产期等）进行分析。

敏感度分析（Sensitivity analysis，也称敏感性分析）是研究数学模型或系统(数值或其他)输出中的不确定性如何在其输入中被分配到不同的不确定性来源。一个相关的实践是不确定度分析，它更注重不确定度的量化和不确定度的传播；理想情况下，不确定度和敏感度分析应该同时进行。

敏感性分析是一种用于了解模型对输入参数变化的敏感程度的方法。在一个数学或计算模型中，输入参数的变化可能会导致模型输出的变化。敏感性分析的目标是识别哪些输入参数对输出产生重要影响，哪些对输出影响较小。

让我们通过一个简单的例子来理解敏感性分析：

假设有一个简单的天气预测模型，它的输入参数包括：

温度
湿度
风速

输出是：

是否会下雨

我们想知道在这个模型中，哪个输入参数对于预测是否会下雨最为关键。

敏感性分析的步骤：

选择参数范围： 确定每个输入参数可能的取值范围。比如，温度在0到40摄氏度之间，湿度在0到100%，风速在0到20米/秒之间。
生成参数组合： 使用敏感性分析工具或方法，生成一系列不同的参数组合，这些组合覆盖了你事先定义的参数范围。
运行模型： 使用生成的参数组合运行天气预测模型，得到相应的输出（是否会下雨）。
分析输出变化： 通过分析输出结果，找出哪个输入参数的变化对于是否下雨有重要影响。可能发现，当温度升高时，更容易下雨；湿度增加也增加了下雨的可能性，而风速对是否下雨的影响较小。
计算敏感性指标： 使用敏感性分析的指标，比如Sobol指数，来量化每个输入参数对输出的影响程度。这些指标提供了一个排序，显示了哪个参数最为重要。

结果解释：

如果某个参数的一阶Sobol指数很大，说明这个参数对输出的影响较大。
如果某个参数的二阶Sobol指数很大，说明这个参数与其他参数的交互作用对输出的影响较大。

通过敏感性分析，我们可以更好地理解模型的行为，确定哪些因素是决定性的，从而在需要调整或优化模型时提供有用的信息。

选择敏感度分析方法的时候需要考虑的要素：

每运行一次模型的计算代价
输入参数之间的相关性
模型的响应是否非线性
输入因素之间的相互作用
-已有数据的输入范围

2. 常见的敏感度分析方法

（跳过了傅里叶分析相关的方法，只有最后两个方法是全局分析）

One at a time(OAT) 方法
每次变动一个输入并检查对于输出的影响。
这种方法很简单，但由于它没有考虑输入变量的同时变化，因此并未充分探索输入空间。也无法检测输入变量之间是否存在交互。
Screening方法
窗口法是一种基于采样的方法。目的是要确定哪些输入变量对高维模型中的输出不确定性有重大影响，而不是准确地量化灵敏度。
它具有相对较低的计算成本，并且可以在对其余集合应用更具信息性的分析之前，用于初步分析中以清除无影响的变量。
最常用的筛选方法之一是基本效应方法（moris方法）
散点图法
基于偏导数的局部分析法
检查输出对于各个输入的偏导数
也无法充分探索输入空间
Adjoint modelling and Automated Differentiation 都属于这类方法
回归分析
在敏感性分析的背景下，回归分析包括将线性回归拟合到模型响应，并使用标准化回归系数作为敏感性的直接度量。
因此，当模型响应实际上是线性时，此方法最合适。例如，如果确定系数大，则可以确认回归模型有效。
回归分析的优点是简单且计算成本低。
基于方差的方法（sabol方法）
是全局方法。可以处理非线性响应，并且可以度量非加性系统中相互作用的影响。
属于概率论方法。可将输入和输出不确定性量化为概率分布，并将输出方差分解为可归因于输入变量和变量组合的部分。因此，输出对输入变量的敏感度通过该输入引起的输出变化量来度量。
常常会涉及蒙特卡洛方法
基于响应面的方差分析（VARS）
这种通过一系列多个变量、确定性的“试验”，来模拟真实极限状态曲面的方法称为响应面法。

3. 关于SALib

SALib（Sensitivity Analysis Library）是一个用于执行全局敏感性分析的Python库。它支持多种敏感性分析方法，其中一种常见的方法是基于Sobol指数的分析。

3.1. Sobol敏感性分析的基本原理

Sobol指数：

Sobol指数是一种衡量输入变量对输出变量方差贡献的方法。它将系统总方差分解为各个输入变量及其组合的贡献。对于一个输入维度为d的系统，Sobol指数可以分为一阶（first-order）、二阶（second-order）和高阶Sobol指数。

一阶Sobol指数：
一阶Sobol指数（S_i）衡量单个输入变量对输出变量方差的贡献，计算公式为：

$S_i = \frac{V[E(Y|X_i)]}{V(Y)}$

其中， $V$ 表示方差， $E$ 表示期望， $Y$ 是输出变量， $X_i$ 是第i个输入变量。

二阶Sobol指数：
二阶Sobol指数（S_{ij}）衡量两个输入变量及其组合对输出变量方差的贡献，计算公式为：

$S_{ij} = \frac{V[E(Y|X_i, X_j)] - S_i - S_j}{V(Y)}$

其中， $X_i$ 和 $X_j$ 是两个不同的输入变量。

总方差分解：
对于d个输入变量，系统的总方差（( V(Y) )）可以分解为各个输入变量及其组合的一阶和二阶Sobol指数之和。

$\sum_{i=1}^{d} S_i + \sum_{i=1}^{d} \sum_{j=i+1}^{d} S_{ij} + \ldots$

3.2. SALib中的使用

SALib使用模特卡洛模拟方法来估计Sobol指数。它通过生成随机样本（采样）来近似期望值和方差。通过多次采样，可以得到Sobol指数的估计值。

具体而言，SALib的使用步骤包括：

定义问题： 定义输入参数的分布和输出函数。
生成样本： 使用Monte Carlo方法生成输入参数的随机样本。
计算输出： 对于每个样本，计算输出变量的值。
计算Sobol指数： 使用这些样本计算Sobol指数的估计值。
分析结果： 分析Sobol指数的结果，了解各个输入变量对输出的影响。

在SALib中，你可以使用不同的采样方法和Sobol指数的估计方法，以满足特定问题的需求。这种全局敏感性分析有助于理解输入变量对输出的影响，优化模型和进行决策。

3.3. 基本解释和评价标准

Sobol敏感性分析的结果通常包括一阶 $S_1$ 和总体 $S_T$ 敏感性指数，这些指数表示了模型输出的变异中各个输入参数的贡献程度。下面是对这些指数的一些基本解释和评价标准：

一阶敏感性指数 $S_1$ ：
- 表示单个参数对输出变异的贡献。
- 范围在[0, 1]之间，值越大表示该参数对输出的影响越显著。
- 如果 $S_1$ 接近于0，表示该参数对输出的影响较小；如果接近于1，表示该参数对输出的影响较大。
总体敏感性指数 $S_T$ ：
- 表示单个参数和该参数与其他参数的相互作用对输出变异的综合贡献。
- 范围在[0, 1]之间，值越大表示该参数及其相互作用对输出的影响越显著。
- 通过 $S_T$ 可以了解整体的输入变异中，多个参数共同贡献了多少。

评价这些指数通常取决于具体的应用和研究目的。一般来说，可以使用以下一些标准进行初步评估：

$S_1$ 和 $S_T$ 的绝对值越大，表示对输出的影响越大。
如果某个参数的 $S_T$ 明显大于 $S_1$ ，则该参数的相互作用较为显著。
如果某个参数的 $S_1$ 明显大于 $S_T$ ，则该参数对输出的影响主要来自于它本身的变异。

需要注意的是，这些指数的评价应该结合具体的背景和模型特性，而且敏感性分析的结果应该被视为对模型的理解的一种贡献，而非唯一的评估标准。

4. SALib实践

4.1. 安装SALib

pip install -i https://pypi.tuna.tsinghua.edu.cn/simple SALib

github地址：
https://github.com/SALib/SALib

4.2. 教程案例一

在本例中，我们将使用SALib主要功能Ishigami函数（如下所示）进行Sobol灵敏度分析。该示例将在下一个教程中重复使用面向对象的界面，可能会发现该界面更容易使用。

Ishigami函数通常用于测试不确定度和灵敏度分析方法，因为它表现出很强的非线性和非单调性。其源代码位于SALib\test_functions\Ishigami.py。对应函数计算公式如下：

$\sin(x_{1}) + A \sin(x_{2})^2 + Bx^{4}_{3}\sin(x_{1})$

示例代码：


from SALib.sample import saltelli
from SALib.analyze import sobol
#from SALib.test_functions import Ishigami
import numpy as np

problem = {
  'num_vars': 3,
  'names': ['x1', 'x2', 'x3'],
  'bounds': [[-np.pi, np.pi]]*3
}

# SALib.test_functions Ishigami.py
def evaluate(X: np.ndarray, A: float = 7.0, B: float = 0.1) -> np.ndarray:
    Y = np.zeros(X.shape[0])
    Y = (
        np.sin(X[:, 0])
        + A * np.power(np.sin(X[:, 1]), 2)
        + B * np.power(X[:, 2], 4) * np.sin(X[:, 0])
    )

    return Y

# Generate samples
param_values = saltelli.sample(problem, 1024)

# Run model (example)
# Y = Ishigami.evaluate(param_values)
Y = evaluate(param_values)

# Perform analysis
Si = sobol.analyze(problem, Y, print_to_console=True)
# Returns a dictionary with keys 'S1', 'S1_conf', 'ST', and 'ST_conf'
# (first and total-order indices with bootstrap confidence intervals)

Si.plot()

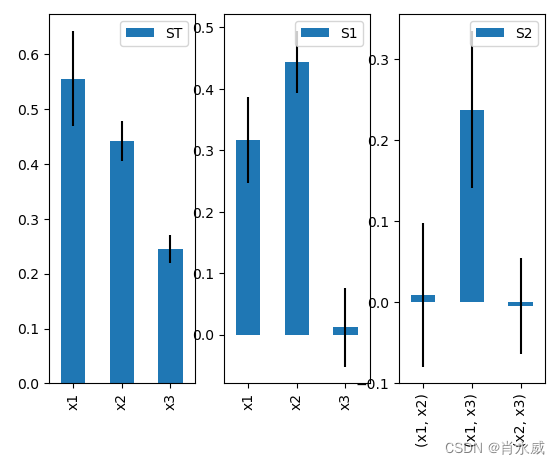
在这里插入图片描述

在SALib库中，sobol.analyze函数用于进行Sobol敏感性分析。以下是一些用到的关键参数和具体介绍：
sobol.analyze(problem, Y, calc_second_order=True, print_to_console=False)

problem：描述问题的字典，包括参数的个数、参数名称和参数范围。
Y：模型的输出，是一个包含对应参数样本的模型输出值的数组。
calc_second_order：一个布尔值，指定是否计算二阶Sobol指数。如果为True，则计算，如果为False，则不计算。
print_to_console：一个布尔值，指定是否将结果打印到控制台。

analyze函数返回一个包含Sobol指数和置信区间的字典。以下是一些重要的输出：

S1：一阶Sobol指数，表示每个输入参数对输出的主导影响。
ST：总Sobol指数，表示每个参数总体上对输出的影响，包括直接和交互作用。
S2：二阶Sobol指数，表示两个参数之间的交互作用对输出的影响。
S2_conf：二阶Sobol指数的置信区间。

使用这些指数，你可以了解每个参数的独立贡献以及不同参数之间的相互作用对输出的影响。对于更详细的信息，你可以参考Sobol敏感性分析的相关文献或SALib文档。

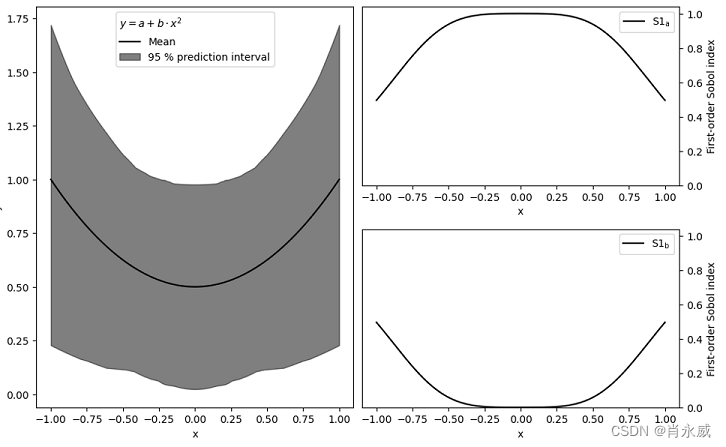
4.3. 教程案例二

当您要分析的模型取决于不属于灵敏度分析的参数时，如位置或时间，可以分别对每个时间/位置进行分析。

以抛物线为例：

$f（x）=a+bx^2$

参数 $a$ 和 $b$ 将接受灵敏度分析，但 $x$ 不会。

import numpy as np
import matplotlib.pyplot as plt

from SALib.sample import saltelli
from SALib.analyze import sobol

def parabola(x, a, b):
    """Return y = a + b*x**2."""
    return a + b*x**2

problem = {
    'num_vars': 2,
    'names': ['a', 'b'],
    'bounds': [[0, 1]]*2
}

# sample
param_values = saltelli.sample(problem, 2**6)
# evaluate
x = np.linspace(-1, 1, 1000)
y = np.array([parabola(x, *params) for params in param_values])
# analyse
sobol_indices = [sobol.analyze(problem, Y) for Y in y.T]

S1s = np.array([s['S1'] for s in sobol_indices])

fig = plt.figure(figsize=(10, 6), constrained_layout=True)
gs = fig.add_gridspec(2, 2)

ax0 = fig.add_subplot(gs[:, 0])
ax1 = fig.add_subplot(gs[0, 1])
ax2 = fig.add_subplot(gs[1, 1])

for i, ax in enumerate([ax1, ax2]):
    ax.plot(x, S1s[:, i],
            label=r'S1$_\mathregular{{{}}}$'.format(problem["names"][i]),
            color='black')
    ax.set_xlabel("x")
    ax.set_ylabel("First-order Sobol index")

    ax.set_ylim(0, 1.04)

    ax.yaxis.set_label_position("right")
    ax.yaxis.tick_right()

    ax.legend(loc='upper right')

ax0.plot(x, np.mean(y, axis=0), label="Mean", color='black')

# in percent
prediction_interval = 95

ax0.fill_between(x,
                 np.percentile(y, 50 - prediction_interval/2., axis=0),
                 np.percentile(y, 50 + prediction_interval/2., axis=0),
                 alpha=0.5, color='black',
                 label=f"{prediction_interval} % prediction interval")

ax0.set_xlabel("x")
ax0.set_ylabel("y")
ax0.legend(title=r"$y=a+b\cdot x^2$",
           loc='upper center')._legend_box.align = "left"

plt.show()

在这里插入图片描述

5. 总结

敏感性分析与AHP结合使用具有重要的应用意义，主要体现在以下几个方面：

决策可靠性评估： 敏感性分析能够评估决策模型对输入参数变化的敏感程度，从而帮助决策者判断模型的可靠性。与AHP结合，可以更全面地评估模型各部分对决策结果的影响，提高决策的准确性和可靠性。
权重调整与优化： 在AHP中，确定因素权重是关键的一步。敏感性分析可以帮助识别模型对不同因素权重变化的响应，为权重的调整提供参考。通过综合敏感性分析结果，优化AHP的判断矩阵，提高决策模型的精度。
风险管理： 敏感性分析有助于识别模型对输入参数变化的敏感程度，从而帮助决策者更好地理解决策的风险。在AHP的框架下，通过分析各因素对决策结果的敏感性，可以有针对性地制定风险管理策略，提高决策的稳健性。
决策方案比较： 敏感性分析可以用于比较不同决策方案在输入参数变化下的表现。结合AHP，可以更全面地考虑不同因素的权重，使决策者更准确地评估各个方案的优劣，有助于选取最优决策方案。
决策过程透明度： 敏感性分析提高了决策模型的透明度，使决策者对模型的运作机制有更清晰的认识。结合AHP，可以将不同因素的权重纳入考虑，使决策过程更加透明，有助于决策者更好地理解和接受决策模型的结果。