数学建模-基于LightGBM和BP神经网络的互联网招聘需求分析与预测
基于LightGBM和BP神经网络的互联网招聘需求分析与预测
整体求解过程概述(摘要)
就业是民生之本,是发展之基,也是安国之策。2020 年新冠肺炎疫情的爆发,稳就业成为应对疫情、稳定社会的重要保障之一。随着数据新动能的发展,互联网招聘为招聘者和应聘者提供不限于时空的全局视角,因此本文从该角度出发对招聘者和应聘者需求进行统计分析预测,以期缓解就业难、招聘难的困境。
本文基于近年来各在线招聘网站所发布的招聘数据并结合数据新动能下转型升级的三个金融行业、互联网行业、生产制造行业,采用 Pearson 相关系数检验初步筛选后运用灰色关联分析进一步进行指标筛选,最后对企业招聘中招聘者关注的浏览量运用 LightGBM 模型进行浏览量特征重要性分析,对就业形势中应聘者关注的薪资运用 BP 神经网络预测模型对于薪资进行预测,并进行模型精度对比,得出数据新动能下三个行业的薪资统计分析预测。
经研究得出关于企业招聘浏览量,金融行业薪资水平,互联网行业薪资水平,生产制造行业薪资水平的影响因素及重要程度。基于以上分析结论,本文在互联网招聘市场中对招聘者与应聘者需求提出以下对策建议:第一,对于企业,招聘者应根据岗位浏览量合理设置招聘要求;第二,对于金融行业,应聘者应根据学历因素合理考虑就业地域;第三,对于互联网行业,应聘者应根据学历因素合理考虑公司性质;第四,对于生产制造行业,应聘者应根据公司所在地合理考虑公司性质。
问题分析
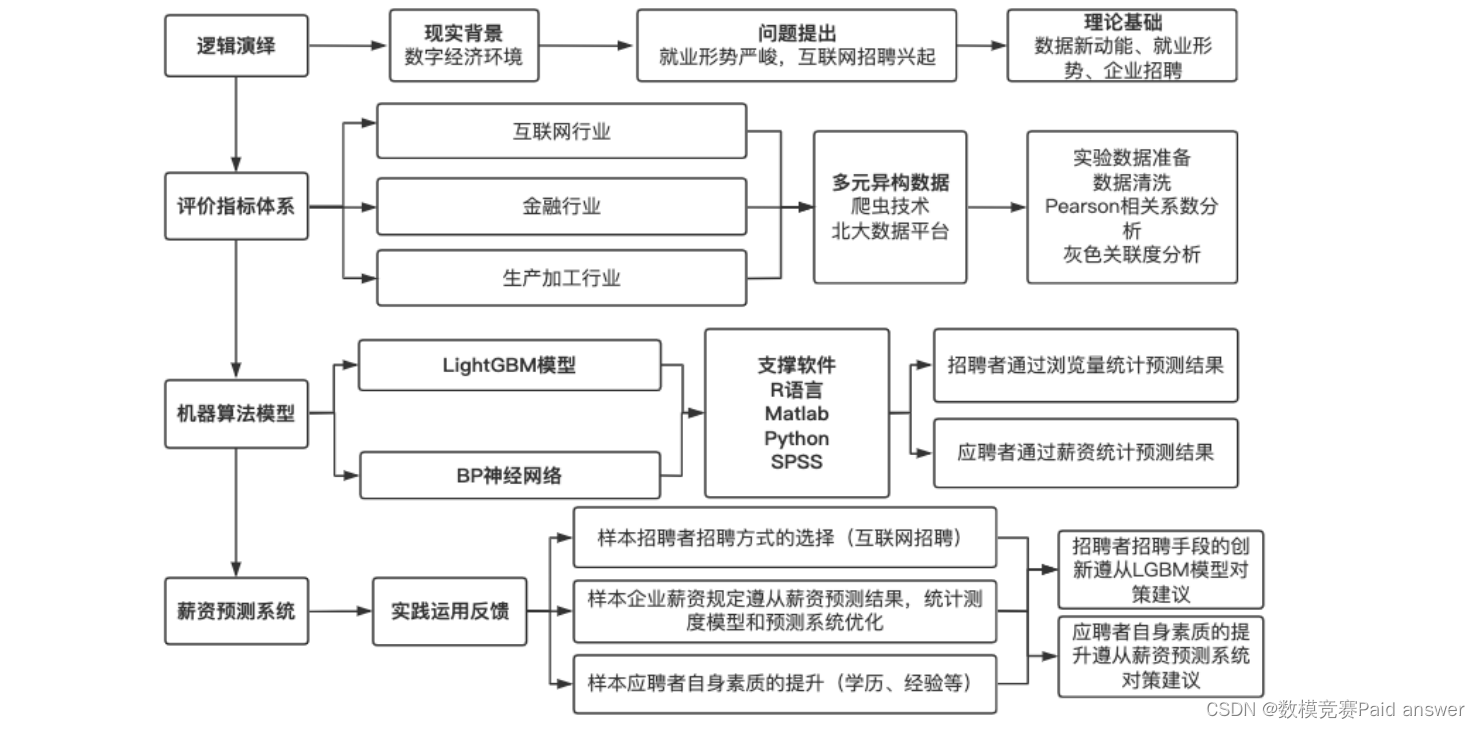
基于当代数字经济大环境背景,面对当前互联网市场应聘者和招聘者需求不对称的现状,本文运用近年来各在线招聘网站所发布的招聘数据并结合数据新动能下转型升级的三个金融行业、互联网行业、生产制造行业,采用 Pearson 相关系数分析初步筛选后运用灰色关联分析进一步进行维度筛选,最后对企业招聘中招聘者关注的浏览量运用 LightGBM 模型进行特征重要性分析,对就业形势中应聘者关注的薪资运用 BP 神经网络预测模型对于薪资进行预测,并进行模型检验与修正,得出新动能下三个行业的薪资和浏览量的分析与预测。
指标的选取与数据的处理
(一)数据来源
本文数据通过对某数据平台的数据进行爬取,总共得到 1007894 条数据。数据预处理以 excel 为主,Python、R 为辅,完成原始数据去重区空以及数值转换等数据预处理工作之后进行分层随机抽样得到剩下 40000 条数据进行统计分析。对于异常值的处理,学历、职位、行业等因素使用删除异常值方法处理,经验年数、工资上下限因素使用计算平均值方法进行处理。分层抽样法,也叫类型抽样法。将总体单位按其属性特征分成若干类型或层,然后在类型或层中随机抽取样本单位。分层抽样法的特点是通过划类分层,增大了各类分层抽样中单位间的共同性,容易抽出具有代表性的调查样本。该方法适用于总体情况复杂,各单位之间差异较大,单位较多的情况。分层随机抽样的程序是把总体各单位分成两个或两个以上的相互独立且各具特点的完全的组,再从两个或两个以上的组中分别进行随机抽样。分组的标志或特点与所关心的总体特征相关。“所学非所用”不利于充分发挥人力资本的潜在价值(郭睿,2019),本文以学历作为属性特征进行分层,将不同学历分出不同层,按各学历占总数据的比例在每一层中随机抽样,得出 40000 条数据。
并通过划分行业来分别选取每个行业中的指标进行分析预测,金融行业的发展是一个国家经济发展的重要支撑(高景文,2019),互联网行业则为数字化时代背景下一个重要的行业支撑(周蕴慧,2021),生产制造行业的转型升级也是当今时代面临的重大课题(江小涓,2020),这三个行业都对数据新动能背景下招聘与就业需求不对称的统计分析研究具有一定意义,因此本文选取这三种行业进行统计分析预测。
而对于大多数互联网应聘者而言,薪资是众多被考虑因素中的重中之重,是其劳动回报的直接体现(Kristin L ,2018),对于企业而言,应聘者的薪资与其经营的利润以及成本是直接相关的关系。因此选取三个行业薪资平均值与其他指标进行分析。
(二)指标选取
1. Pearson 相关系数检验
Pearson 相关系数是用协方差除以两个变量的标准差得到的,虽然协方差能反映两个随机变量的相关程度(协方差大于 0 的时候表示两者正相关,小于 0 的时候表示两者负相关),但是协方差值的大小并不能很好地度量两个随机变量的关联程度,对于标准化后的数据求欧氏距离平方并经过简单的线性变化,也就是Pearson 系数,我们一般用欧式距离来衡量向量的相似度,但欧式距离无法考虑不同变量间取值的差异。加之,Pearson 相关系数适用于高维度检验,而未经升级的欧式距离以及 cosine 相似度,对变量的取值范围是敏感的,在使用前需要进行适当的处理。因此在对变量间进行相关性检验时,本文优先采用 Pearson 相关系数检验去研究经验,学历,公司所在地,公司性质,职位分别和薪资平均值之间的相关关系,使用 Pearson 相关系数去表示相关关系的强弱情况。具体分析可知:
①金融行业:经验、学历、职位、公司所在地呈现显著性

②互联网行业:经验、学历、职位、公司所在地、公司性质呈现显著性

③生产制造行业:经验、学历、公司所在地、公司性质呈现显著性

2. 灰色关联分析
基于 Pearson 相关系数检验得出的结果,本文进一步对具有显著性的各个特征值进行选取。运用灰色关联分析对于研究指标进行进一步选取,研究各因素对薪资的影响大小关系,得出结果如下:
①金融行业:公司所在地、职位
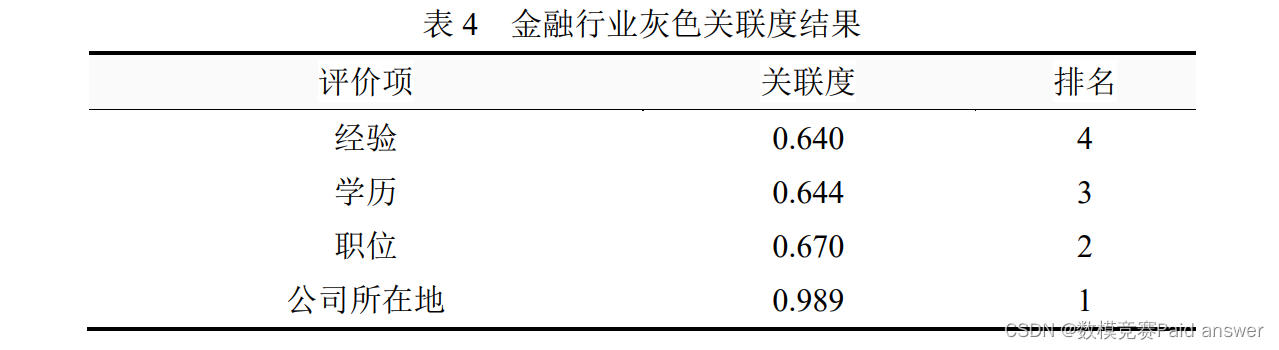
从上表可以看出:针对本次 4 个评价项,公司所在地的综合评价最高(关联度为:0.989),其次是职位(关联度为:0.670)。
②互联网行业:学历、公司性质

从上表可以看出:针对本次 5 个评价项,学历的综合评价最高(关联度为:0.928),其次是公司性质(关联度为:0.909)。
③生产制造行业:公司所在地、公司性质
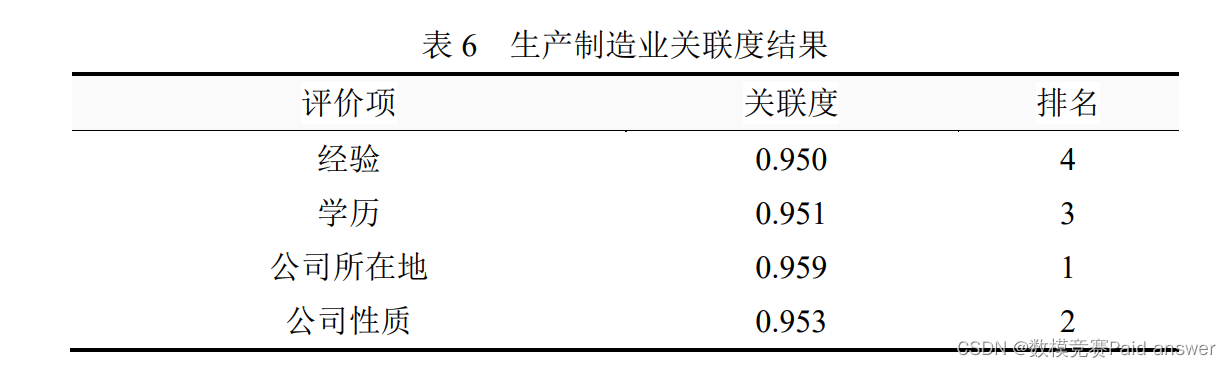
从上表可以看出:针对本次 4 个评价项,公司所在地的综合评价最高(关联度为:0.959),其次是公司性质(关联度为:0.953)
模型的建立与求解整体论文缩略图


全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:(代码和文档not free)
%% 网络测试
an=sim(net,inputn_test); %用训练好的模型进行仿真
test_simu=mapminmax('reverse',an,outputps); % 预测结果反归一化
error=test_simu-output_test; %预测值和真实值的误差
%%真实值与预测值误差比较
figure
plot(output_test,'bo-','linewidth',1.2)
hold on
plot(test_simu,'r*-','linewidth',1.2)
legend('期望值','预测值')
xlabel('测试样本编号'),ylabel('指标值')
title('BP 测试集预测值和期望值的对比')
set(gca,'fontsize',12)
igure
plot(error,'ro-','linewidth',1.2)
xlabel('测试样本编号'),ylabel('预测偏差')
title('BP 神经网络测试集的预测误差')
set(gca,'fontsize',12)
%计算误差
[~,len]=size(output_test);
SSE1=sum(error.^2);
MAE1=sum(abs(error))/len;
MSE1=error*error'/len;
RMSE1=MSE1^(1/2);
MAPE1=mean(abs(error./output_test));
r=corrcoef(output_test,test_simu); %corrcoef 计算相关系数矩阵,包括自相关和
互相关系数
R1=r(1,2);
%% 初始化
clear
close all
clc
format short
%% 读取读取
data=xlsread('数据总.xlsx','Sheet1','A1:F18528'); %%使用 xlsread 函数读取 EXCEL
中对应范围的数据即可
%输入输出数据
input=data(:,1:end-1); %data 的第一列-倒数第二列为特征指标
output=data(:,end); %data 的最后面一列为输出的指标值
N=length(output); %全部样本数目
testNum=50; %设定测试样本数目
trainNum=N-testNum; %计算训练样本数目
%% 划分训练集、测试集
input_train = input(1:trainNum,:)';
output_train =output(1:trainNum)';
input_test =input(trainNum+1:trainNum+testNum,:)';
output_test =output(trainNum+1:trainNum+testNum)';
%% 数据归一化
[inputn,inputps]=mapminmax(input_train,0,1);
[outputn,outputps]=mapminmax(output_train);
inputn_test=mapminmax('apply',input_test,inputps);
%% 获取输入层节点、输出层节点个数
inputnum=size(input,2);
outputnum=size(output,2);
disp('/')
disp('神经网络结构...')
disp(['输入层的节点数为:',num2str(inputnum)])
disp(['输出层的节点数为:',num2str(outputnum)])
disp(' ')
disp('隐含层节点的确定过程...')
%确定隐含层节点个数
%采用经验公式 hiddennum=sqrt(m+n)+a,m 为输入层节点个数,n 为输出层节点
个数,a 一般取为 1-10 之间的整数
MSE=1e+5; %初始化最小误差
transform_func={'tansig','purelin'}; %激活函数
train_func='trainlm'; %训练算法
for
hiddennum=fix(sqrt(inputnum+outputnum))+1:fix(sqrt(inputnum+outputnum))+10
%构建网络
net=newff(inputn,outputn,hiddennum,transform_func,train_func);
% 网络参数
net.trainParam.epochs=1000; % 训练次数
net.trainParam.lr=0.01; % 学习速率
net.trainParam.goal=0.000001; % 训练目标最小误差
% 网络训练
net=train(net,inputn,outputn);
an0=sim(net,inputn); %仿真结果
mse0=mse(outputn,an0); %仿真的均方误差
disp([' 隐含层节点数为 ',num2str(hiddennum),' 时,训练集的均方误差为:
',num2str(mse0)])
%更新最佳的隐含层节点
if mse0<MSE
MSE=mse0;
hiddennum_best=hiddennum;
end
end
disp(['最佳的隐含层节点数为:',num2str(hiddennum_best),',相应的均方误差为:
',num2str(MSE)])
%% 构建最佳隐含层节点的 BP 神经网络
net=newff(inputn,outputn,hiddennum_best,transform_func,train_func);
% 网络参数
net.trainParam.epochs=1000; % 训练次数
net.trainParam.lr=0.01; % 学习速率
net.trainParam.goal=0.000001; % 训练目标最小误差
%% 网络训练
net=train(net,inputn,outputn);
%% 网络测试
an=sim(net,inputn_test); %用训练好的模型进行仿真
test_simu=mapminmax('reverse',an,outputps); % 预测结果反归一化
error=test_simu-output_test; %预测值和真实值的误差
%%真实值与预测值误差比较
figure
plot(output_test,'bo-','linewidth',1.2)
hold on
plot(test_simu,'r*-','linewidth',1.2)
legend('期望值','预测值')
xlabel('测试样本编号'),ylabel('指标值')
title('BP 测试集预测值和期望值的对比')
set(gca,'fontsize',12)
figure
plot(error,'ro-','linewidth',1.2)
xlabel('测试样本编号'),ylabel('预测偏差')
title('BP 神经网络测试集的预测误差')
set(gca,'fontsize',12)
%计算误差
[~,len]=size(output_test);
SSE1=sum(error.^2);
MAE1=sum(abs(error))/len;
MSE1=error*error'/len;
RMSE1=MSE1^(1/2);
MAPE1=mean(abs(error./output_test));
r=corrcoef(output_test,test_simu); %corrcoef 计算相关系数矩阵,包括自相关和
互相关系数
R1=r(1,2);
disp(' ')
disp('/')
disp('预测误差分析...')
disp(['误差平方和 SSE 为: ',num2str(SSE1)])
disp(['平均绝对误差 MAE 为: ',num2str(MAE1)])
disp(['均方误差 MSE 为: ',num2str(MSE1)])
disp(['均方根误差 RMSE 为: ',num2str(RMSE1)])
disp(['平均百分比误差 MAPE 为: ',num2str(MAPE1*100),'%'])
disp(['相关系数 R 为: ',num2str(R1)])
%打印结果
disp(' ')
disp('/')
disp('打印测试集预测结果...')
disp([' 编号 实际值 预测值 误差'])
for i=1:len
disp([i,output_test(i),test_simu(i),error(i)])
end
