一维卷积与一维平均池化的时间复杂度
计算请参考这篇文章:
(284条消息) 卷积神经网络的时间、空间复杂度以及数据流的变化_卷积的时间复杂度_Briwisdom的博客-CSDN博客
1. 时间复杂度
时间复杂度即模型的运行次数。
单个卷积层的时间复杂度:Time~O(M^2 * K^2 * Cin * Cout)
//有的好奇小宝宝可能问到为什么计算复杂度是O(M^K^2),请往下读,读到最后你会知道。
M:输出特征图(Feature Map)的尺寸。
K:卷积核(Kernel)的尺寸。
Cin:输入通道数。
Cout:输出通道数。
注1:为了简化表达式变量个数,统一假设输入和卷积核的形状是正方形,实际中如果不是,则将M ^2替换成特征图的长宽相乘即可;
注2:每一层卷积都包含一个偏置参数(bias),这里也给忽略了。加上的话时间复杂度则为:O(M^2 * K^2 * Cin * Cout+Cout)。
在咱们这个1维度情况里面,M与K都是一维度,可以理解为长为M,宽为1的情况,K也同理,Cin=Cout=1。那么1D-CNN的时间复杂度为Time~O(M*K*1*1)
举个例子,长度为L的序列,经过1D-卷积[kernel=stride=i,padding=i/2],(i∈{L/2,L/4,...}),
为了方便理解,我们假设i=L/2,那么经过计算得到M=2(该计算过程请参考下方输出长度计算),
又∵K=i=L/2 ∴ 该情况下的1D-CNN时间复杂度为Time~O(2*(L/2))=O(L)
//回到上一个话题,关于为什么计算复杂度是O(M^K^2),那你目前肯定知道1D-CNN的Time~O(M*K*1*1)怎么来的了,你又好奇为什么M是输出长度,K是卷积核了吧,其实你可以这么理解,你知道时间复杂度就是加法或者乘法的总数,输出长度为M,就说明有M次计算,而每次计算都会分别有K次加法和K次乘法,只不过2是常数可以忽略不计,在计算时间复杂度的时候,这样理解了吧!还不理解欢迎评论留言。
2.输出长度
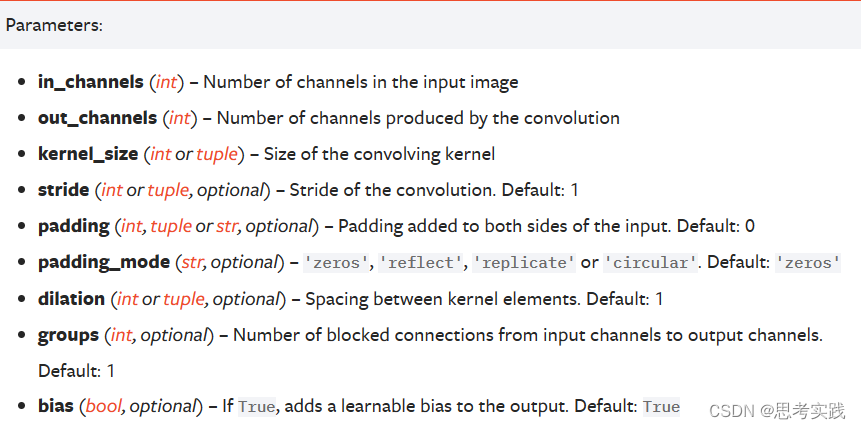
输出长度看Pytorch官方文档就懂了: 一维全局平均池化的输出长度是1维卷积dilation=1(default)的情况
1维卷积

 1维平均池化
1维平均池化

参考资料
Conv1d — PyTorch 2.0 documentation
AvgPool1d — PyTorch 2.0 documentation(284条消息) 神经网络时间复杂度和空间复杂度(参数量计算和计算量计算)_放牛娃不吃草的博客-CSDN博客
