[LeetCode周赛复盘] 第 374 场周赛20231203

一、本周周赛总结

• 比赛后才做出T3，没敢交
• T1 模拟。
• T2 贪心+分类讨论。
• T3 26维前缀和+枚举。
• T4 组合数学。

100144. 找出峰值

100144. 找出峰值

1. 题目描述

2. 思路分析

按题意模拟即可。

3. 代码实现

class Solution:
    def findPeaks(self, a: List[int]) -> List[int]:
        return [i for i in range(1,len(a)-1) if a[i-1] < a[i] > a[i+1]]

100153. 需要添加的硬币的最小数量

100153. 需要添加的硬币的最小数量

1. 题目描述

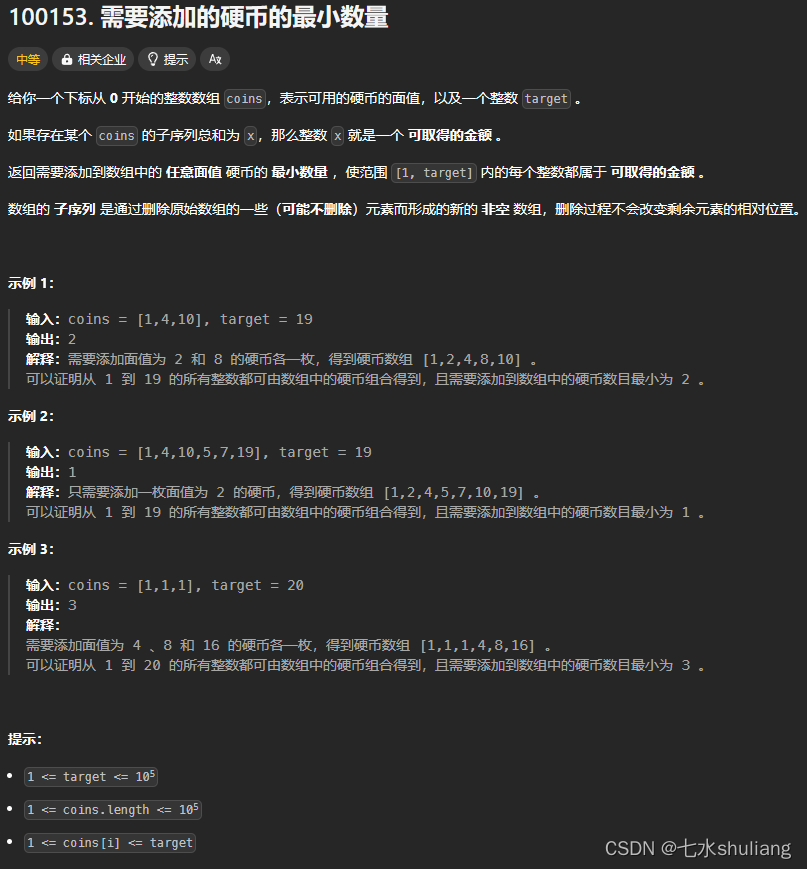
2. 思路分析

分类讨论

• 先把数据排序，从小到大处理。
• 假设当前我们已经得到了[0,s)之间所有的整数。下一个要添加的数x。
  • 添加后可以新获得[x,x+s)之间所有的数。
• 若x<=s,则可以获得[0,x+s)。
• 若x>s, 则无法得到s,必须添加s，得到[0,s+s)。

• 时间复杂度O(nlgn+lgtarget),
• 解释其中lgtarget：若coins为空，那么我们必须自己构造1 2 4 8相当于给target二进制分解。

3. 代码实现

class Solution:
    def minimumAddedCoins(self, coins: List[int], target: int) -> int:
        coins.sort()
        n = len(coins)
        ans = 0 
        i = 0
        s = 1
        while s <= target:
            if i < n and coins[i] <= s:
                s += coins[i]
                i += 1
            else:
                s += s 
                ans += 1
        return ans

100145. 统计完全子字符串

100145. 统计完全子字符串

1. 题目描述

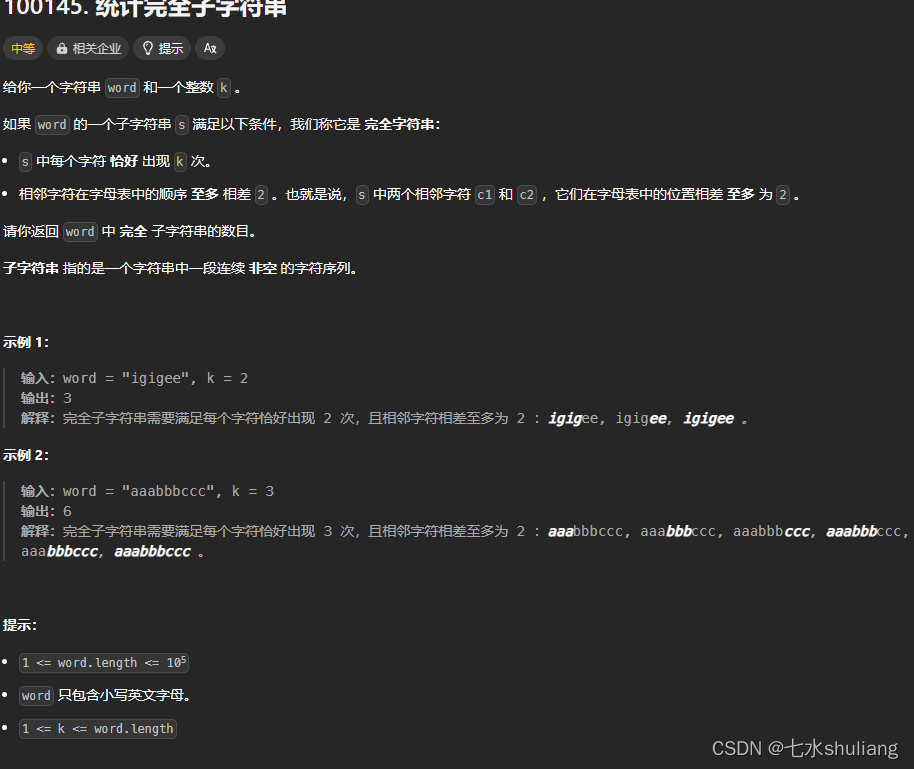
2. 思路分析

 被这题干趴了。一开始写了个滑窗一直wa。

• 这题的难点主要在于计算复杂度，敢不敢暴力。
• 观察合法子串性质，发现子串长度一定是k的倍数，而且最多是26k。再大的话，一定有字母的出现次数超过k了。
• 枚举每个位置作为子串的最后一个字符，左端点每次向前跳k，能否快速计算这段里的每个字符的出现次数？
  • 对每个字符单独做前缀和，用一个26*(n+1)的数组存。
  • 这样计算的次数是26。
• 另外注意，相邻字符差不能超过2，因此左端点向前跳时不能超过这段的开头。
• 实现时，把原串先改写成0~25的数字。

• 时间复杂度O(n2626)。最多比较26次（向前跳），每次比较花费26。

3. 代码实现

class Solution:
    def countCompleteSubstrings(self, word: str, k: int) -> int:
        n = len(word)
        a = [ord(c) - ord('a') for c in word]
        cnt = [[0] * 26 for _ in range(n+1)]
        for i, v in enumerate(a):
            cnt[i+1] = cnt[i][:]
            cnt[i+1][v] += 1
        ans = 0
        start = 0  # 当前连续段的开头(相邻差<=2)
        for i, v in enumerate(a):
            if i and abs(v-a[i-1]) > 2:  # 重开一段
                start = i 
            j = i - k + 1  # 往前跳
            over_k = False  # 有一个字符数量已经超过k
            while j >= start and not over_k:
                for x,y in zip(cnt[i+1],cnt[j]):
                    if x-y>k:
                        over_k = True 
                        break
                    if x-y > 0 and x - y != k :
                        break
                else:
                    ans += 1
                j -= k
        
        return ans 

100146. 统计感冒序列的数目

100146. 统计感冒序列的数目

1. 题目描述

2. 思路分析

组合数学

• m = len(sick)个病人把 整个数组分割成m+1段，只讨论不为空的段。
• 处于中间的段，长为k，自己的传染顺序方案有pow(2,k-1)种，即每次要么感染左端，要么感染右端，当长为1时，左右等价。
• 一共n-m个健康人，从这个序列中选k个位置，作为这组的人的位置，共C(n-m,k)种方案。
  • 安排完这一组，安排下一组时，是从n-m-k中选k’个位置。
• 然后讨论处于两端的段，他们只有一个传染方向，因此自己的顺序只有一种，但要讨论位置方案。

• 其中组合数直接贴逆元模板。
• 初始化放里边竟然会TLE，难绷

3. 代码实现

class ModComb:
    """通过O(n)预处理逆元，达到O(1)询问组合数"""
    def __init__(self, n, p):
        """
        初始化，为了防止模不一样，因此不写默认值，强制要求调用者明示
        :param n:最大值
        :param p: 模
        """
        self.p = p
        self.inv_f, self.fact = [1] * (n + 1), [1] * (n + 1)
        inv_f, fact = self.inv_f, self.fact
        for i in range(2, n + 1):
            fact[i] = i * fact[i - 1] % p
        inv_f[-1] = pow(fact[-1], p - 2, p)
        for i in range(n, 0, -1):
            inv_f[i - 1] = i * inv_f[i] % p

    def comb(self, m, r):
        if m < r or r < 0:
            return 0
        return self.fact[m] * self.inv_f[r] % self.p * self.inv_f[m - r] % self.p
MOD = 10 ** 9 + 7 
mc = ModComb(10**5 + 5, MOD)
class Solution:
    def numberOfSequence(self, n: int, sick: List[int]) -> int:
        ans = 1 
        s = n - len(sick)
        for x,y in pairwise(sick):
            v = y - x -1
            if v:
                ans = ans * mc.comb(s,v) % MOD * pow(2,v-1,MOD) % MOD 
                s -= v 
        ans = ans * mc.comb(s,sick[0]) % MOD
        return ans % MOD       

参考链接