2023年亚太杯APMCM数学建模大赛B题玻璃温室小气候调控

2023年亚太杯APMCM数学建模大赛

B题 玻璃温室小气候调控

原题再现

  温室作物的产量受各种气候因素的影响，包括温度、湿度和风速[1]。其中，适宜的温度和风速对植物生长至关重要[2]。为了调节玻璃温室内的温度、风速等气候因素，在温室设计中常用带风机的通风系统，如图1所示。温室风机的位置和热风出口的速度影响着温室内速度场和温度场的分布和均匀性。因此，如何优化温室风机以获得合适的风速和温度，提高其均匀性，是当前玻璃温室设计中需要解决的重要问题。

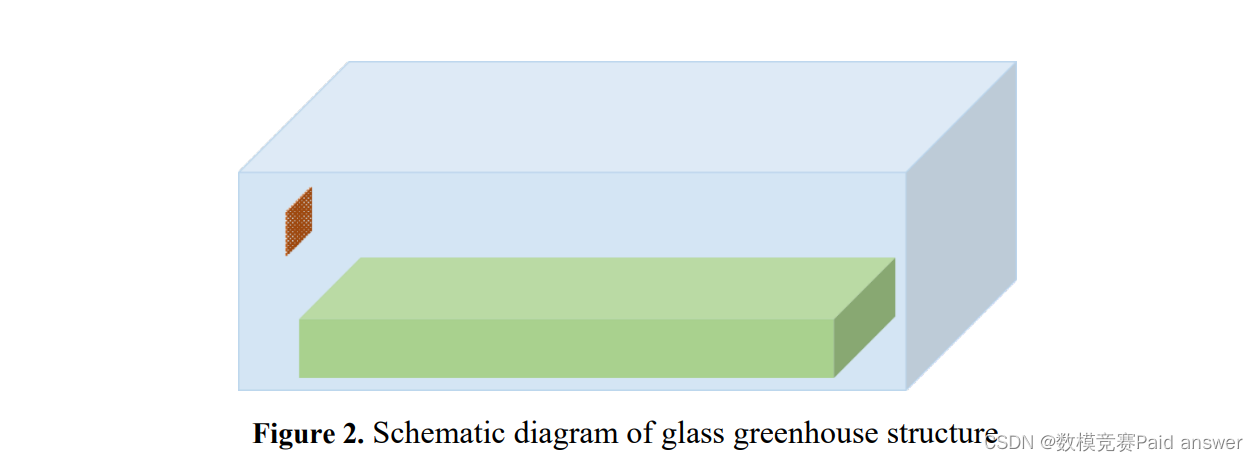
  玻璃温室是密封放置在室内，不考虑外界因素，如温室门、通风、太阳辐射等环境因素。目前设计的玻璃温室尺寸为10m、3m、2m（长、宽、高），温室风机尺寸为0.5m、0.5m，位于温室左侧。温室风扇的中心位于地面上方1.3m处，如图2所示。温室风机侧的边界条件设为速度入口条件，水平方向吹40”暖风，平均风速2 m/s，温室外玻璃和底土设为墙体条件，主要通过对流换热和传导与整个温室进行能量交换[3]，初始温度设为20”。在温室内种植作物时，必须考虑作物的冠层阻力。作物模型可以简化为一个尺寸为8m、2m、0.5m（长、宽、高）的多孔介质，放置在温室中心。温室内作物生长适宜风速为0.3-1m/s，适宜温度为23-26”。

  问题1：请建立无作物玻璃温室内温度和风速分布的数学模型。在0.5米高度的温室横截面上显示风速和温度分布。

  问题2：请建立种植作物的玻璃温室内温度和风速分布的数学模型。展示温室内两个横截面的风速和温度分布：一个在0.5米高度（作物冠层水平）处，另一个在0.1米高度（作物冠层内）。分析条件是否适合作物生长。

  问题3：请提供以下两种情况下玻璃温室内的温度和风速分布，并与第二个问题中给出的解决方案进行比较。在方案一中，将热风出口速度从2 m/s提高到3 m/s。在场景2中，通过将温室风扇从1.3 m移动到1 m来降低其位置。

  问题4：您的团队能否从温室风扇的数量、位置、风速、吹风温度、规格和不同作物等因素进一步优化玻璃温室的温室风扇设计。

function  money =  sumd_money(way,freight,M,b)

   index = unique(way);  
   money = sum(freight(index)); 

    for i = 1:b 
        money = money + M(way(i),i);  
    end
end

function way1 = gen_new_way(way0, s, b)
% way0：原来的买书方案，是一个1*b的向量，每一个元素都位于1-s之间
        index =  randi([1, b],1) ;  % 看哪一本书要更换书店购买
        way1 = way0;  % 将原来的方案赋值给way1
        way1(index) = randi([1, s],1);  % 将way1中的第index本书换一个书店购买   
end

clear; clc   
% 导入书的价格
% 这个数据文件里面保存了两个矩阵：
[s, b] = size(M);  % s
T0 = 1000;   % 初始温度
T = T0; % 迭代中温度会发生改变，第一次迭代时温度就是T0
k_total= 1000;  % 最大迭代次数
Lk = 300;  % 每个温度下的迭代次数
yita = 0.95;  % 温度衰减系数
way0 = randi([1, s],1,b); % 在1-s这些整数中随机抽取一个1*b的向量，表示这b本书分别在哪家书店购买
zhong_way = way0; %用来做中间计算
zhong_money = sumd_money(way0,freight,M,b);%zhong_money用来储存数值，sumd_money为函数计算，在上面可以看到，freight是快递费矩阵

for iter = 1 : k_total  % 外循环, 我这里采用的是指定最大迭代次数
    for i = 1 : Lk  %  内循环，在每个温度下开始迭代
        money0 = sumd_money(way0,freight,M,b); % 调用我们自己写的sum_money函数计算这个方案的花费
        way1 = gen_new_way(way0,s,b);  % 调用我们自己写的gen_new_way函数，也在上面
        money1 = sumd_money(way1,freight,M,b); % 计算新方案
        if money1 < money0    % 如果新方案小于当前方案
            way0 = way1; % 更新当前方案为新方案
            zhong_way = [zhong_way;way1]; % 将新找到的way1添加到中间结果中
            zhong_money = [zhong_money; money1];  % 将新找到的money1添加到中间结果中
        else
            p = exp(-(money1 - money0)/T); % 根据Metropolis准则计算一个概率
            if rand(1) < p   % 生成一个随机数和这个概率比较，如果该随机数小于这个概率
                way0 = way1;  % 更新当前方案为新方案
            end
        end
    end
    T = yita*T;   % 温度下降       
end


[best_money, ind] = min(zhong_money);  
min_way = zhong_way(ind,:); 
disp('最佳的方案是：'); disp(min_way)
disp('此时最优值是：'); disp(best_money)