【知识】稀疏矩阵是否比密集矩阵更高效?
转载请注明出处:小锋学长生活大爆炸[xfxuezhang.cn]
问题提出
有些地方说,稀疏图比密集图的计算效率更高,真的吗?
原因猜想
这里的效率高,应该是有前提的:当使用稀疏矩阵的存储格式(如CSR)时,计算效率更高。如果是普通的完整矩阵格式,实际上效率一样。
稀疏矩阵的存储格式(如 COO、CSR 或 CSC)直接影响乘法的效率, 一些格式在某些类型的运算中更高效,因为它们可以更快地访问和处理非零元素。因此,当使用了稀疏矩阵存储格式时,如果矩阵非常稀疏(即大多数元素为零),那么使用稀疏矩阵进行矩阵乘法通常会更高效,因为可以跳过大量的零元素乘法操作。
代码验证
import numpy as np
from scipy.sparse import csr_matrix
import time
import matplotlib.pyplot as plt
from tqdm import tqdm
def measure_time(matrix_size=1000, density=0.1):
# 创建密集矩阵
dense_matrix = np.random.rand(matrix_size, matrix_size)
# 创建普通的稀疏矩阵
sparse_matrix = dense_matrix < density
sparse_matrix = sparse_matrix.astype(np.float64)
# 将普通的稀疏矩阵转换为CSR格式
csr_matrix_sparse = csr_matrix(sparse_matrix)
# warmup
for _ in range(5):
np.dot(sparse_matrix, sparse_matrix)
# 对普通的稀疏矩阵进行矩阵乘法,并计时
start_time = time.time()
_ = np.dot(sparse_matrix, sparse_matrix)
sparse_time = time.time() - start_time
# warmup
for _ in range(5):
np.dot(dense_matrix, dense_matrix)
# 对密集矩阵进行矩阵乘法,并计时
start_time = time.time()
_ = np.dot(dense_matrix, dense_matrix)
dense_time = time.time() - start_time
# warmup
for _ in range(5):
csr_matrix_sparse.dot(csr_matrix_sparse)
# 对CSR格式的稀疏矩阵进行矩阵乘法,并计时
start_time = time.time()
_ = csr_matrix_sparse.dot(csr_matrix_sparse)
csr_time = time.time() - start_time
return sparse_time, dense_time, csr_time
# 矩阵大小范围
sizes = np.arange(10, 1001, 10)
# 记录每种大小下的耗时
times_sparse = []
times_dense = []
times_csr = []
for size in tqdm(sizes):
sparse_time, dense_time, csr_time = measure_time(matrix_size=size)
times_sparse.append(sparse_time)
times_dense.append(dense_time)
times_csr.append(csr_time)
# 绘制结果
plt.figure(figsize=(10, 6))
plt.plot(sizes, times_sparse, label='sparse')
plt.plot(sizes, times_dense, label='dense')
plt.plot(sizes, times_csr, label='csr')
plt.xlabel('matrix size')
plt.ylabel('time (s)')
plt.title('matrix_size vs time')
plt.legend()
plt.show()
# 稀疏度范围
density = np.arange(0, 1, 0.01)
# 记录每种大小下的耗时
times_sparse = []
times_dense = []
times_csr = []
for den in tqdm(density):
sparse_time, dense_time, csr_time = measure_time(density=den)
times_sparse.append(sparse_time)
times_dense.append(dense_time)
times_csr.append(csr_time)
# 绘制结果
plt.figure(figsize=(10, 6))
plt.plot(density, times_sparse, label='sparse')
plt.plot(density, times_dense, label='dense')
plt.plot(density, times_csr, label='csr')
plt.xlabel('density')
plt.ylabel('time (s)')
plt.title('density vs time')
plt.legend()
plt.show()
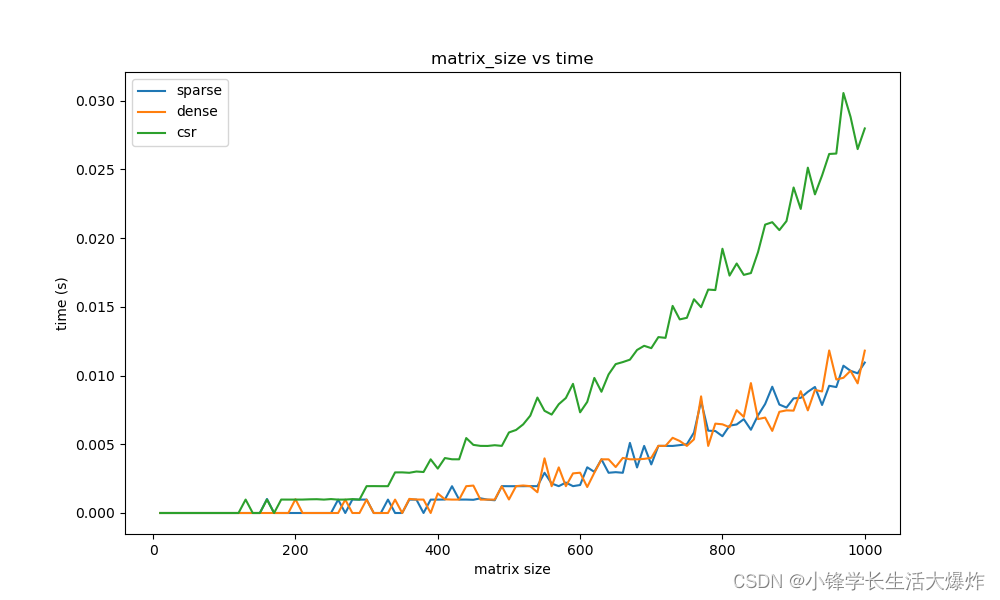
从上图可以看出,随着矩阵大小的增大,三种形式的计算效率都在降低,但两种普通的完整矩阵形式的乘法,其效率的变化趋势是一致的。考虑到时间统计有波动,因此可以看成他俩实际上是一样的时间。
注意,上图中CSR的计算效率低于其他两者,是因为密集度为0.1。当密集度设置为0.01时,CSR的计算效率就会更高了。
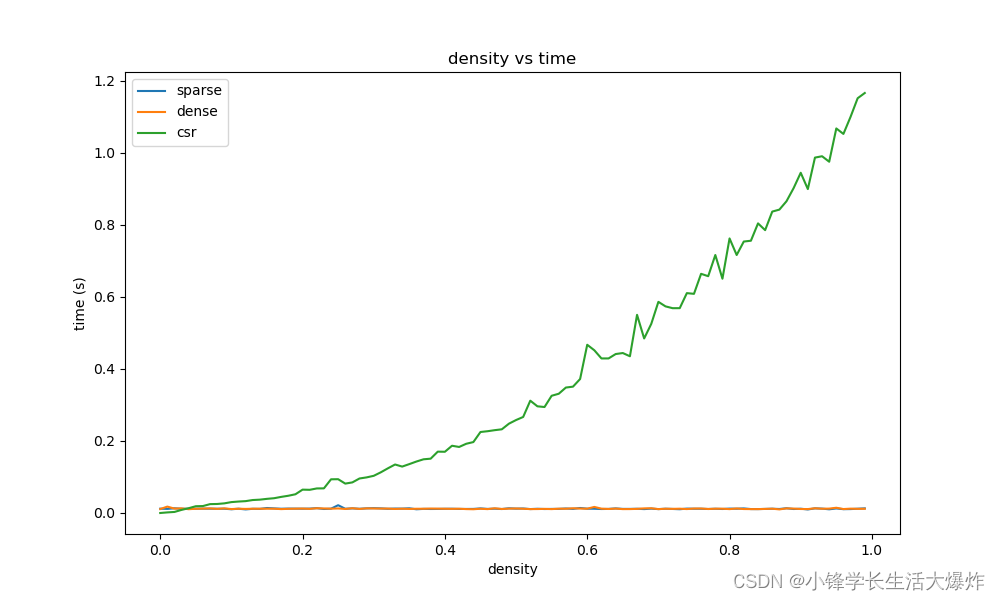
从这个图可以看到,随着密集度的增加,CSR的效率逐渐变低,但普通的完整矩阵形式的乘法,其效率并没有发生变化。
