AC自动机
AC自动机
关键数组
- ne[u]数组:
(1)存节点u的回跳边
(2)所指节点是当前节点的最长后缀
(3)回跳边指向父节点的回跳边所指节点的儿子
- ch[u]数组:
(1)ch[u][i]存节点u沿i走的转移边或者树边
(2)所指节点一定是当前节点的最短路
(3)转移边指向当前节点的回跳边所指节点的儿子
模板代码
import java.util.ArrayDeque;
import java.util.Queue;
import java.util.Scanner;
public class okAC自动机 {
static int N = 500010;
static int cnt[] = new int[N];
static int ch[][] = new int[N][26];
static int ne[] = new int[N];
static int tot;
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
String string;
for(int i = 0;i < n;i++) {
string = scanner.next();
tire(string);
}
build_ac();
string = scanner.next();
int ans = query_ac(string);
System.out.println(ans);
}
//查询出现过的模式串
private static int query_ac(String string) {
// TODO Auto-generated method stub
int ans = 0;
for(int k = 0,i = 0;k < string.length();k++) {
i = ch[i][string.charAt(k)-'a'];
for(int j = i;j != 0 && cnt[j] != -1;j = ne[j]) {
ans += cnt[j];
cnt[j] = -1;
}
}
return ans;
}
//建ac自动机
private static void build_ac() {
// TODO Auto-generated method stub
Queue<Integer> queue = new ArrayDeque<Integer>();
for(int i = 0;i < 26;i++) if(ch[0][i]!=0) queue.add(ch[0][i]);
while (!queue.isEmpty()) {
int u = queue.poll();
for(int i = 0;i < 26;i++) {
int v = ch[u][i];
if(v!=0) {
ne[v] = ch[ne[u]][i];queue.add(v);//节点u存在沿i走的树边,则给对应的儿子节点v建回跳边,并把儿子节点入队
}else {
ch[u][i] = ch[ne[u]][i];//节点u不存在沿i走的树边,则给节点u建沿i走的转移边
}
}
}
}
//建字典树
private static void tire(String string) {
// TODO Auto-generated method stub
int p = 0;
for(int i = 0;i < string.length();i++) {
int c = string.charAt(i)-'a';
if(ch[p][c]==0) ch[p][c] = ++tot;
p = ch[p][c];
}
cnt[p]++;
}
}
深入理解
ne[u]数组
(1)存节点u的回跳边
(2)所指节点是当前节点的最长后缀---------->为什么要设置这个数组
(3)回跳边指向父节点的回跳边所指节点的儿子---------->为什么这么求
假设某AC自动机如下图所示:
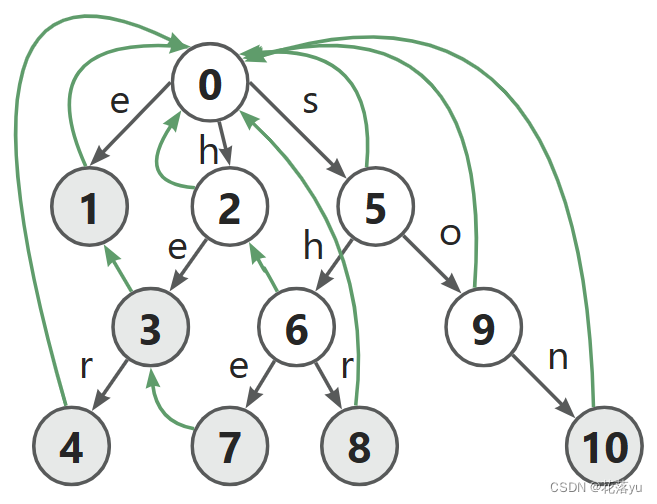
问题(3)
节点7表示的字符串是she,它的最长后缀是he,节点7的父节点6表示的字符串是sh,我们看she的最长后缀和sh的最长后缀的关系,我们可以发现,she的最长后缀就是sh的最长后缀h,然后沿着e走到的节点,对应关系如下:
- 节点7的父节点6表示的字符串是sh----------指向父节点
- 父节点6表示的字符串sh的最长后缀是h----------指向父节点的回跳边所指节点
- 父节点6表示的字符串sh的最长后缀是h沿着e走到了节点3----------指向父节点的回跳边所指节点的儿子(这个儿子一定是沿着e走的)
节点3表示的字符串为he,恰好是she的最长后缀,这个过程其实形成了一个四边形,如下:
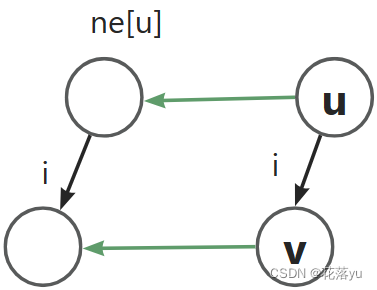
问题(2),我们要先看模式串匹配的过程
private static int query_ac(String string) {
// TODO Auto-generated method stub
int ans = 0;
for(int k = 0,i = 0;k < string.length();k++) {
i = ch[i][string.charAt(k)-'a'];
for(int j = i;j != 0 && cnt[j] != -1;j = ne[j]) {
ans += cnt[j];
cnt[j] = -1;
}
}
return ans;
}
通过for循环代码:for(int j = i;j != 0 && cnt[j] != -1;j = ne[j]) 我们可以看出每次沿着主串走到一个点i,我都要沿着节点i的回跳边走,直到某个回跳边指向的节点为0,即根节点,这个时候才停止。我们为什么要沿着回跳边走呢?我们来模拟一下
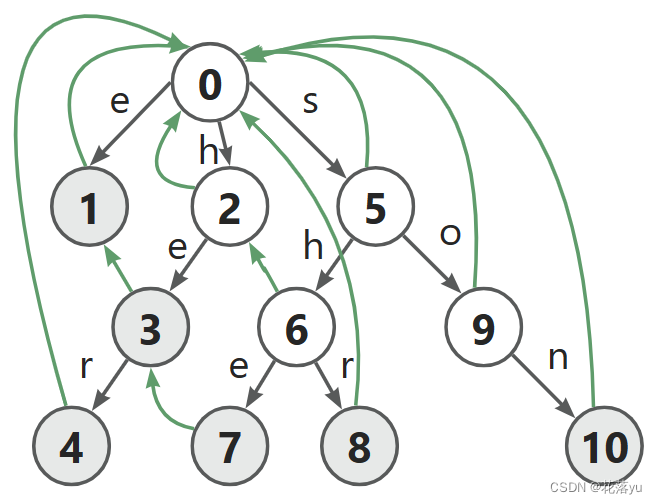
假设我们的主串是she,此时我们走到了节点7,可以看到节点7被标记了,那么我们已经找到了一个模式串,但是只有这一个模式串吗?不是的,从图中我们可以看出he和e也是模式串,并且也可以在she里被找到,he是she的回跳边指向的节点,也是she的最长后缀,那么其实这就是ne数组的作用了。
当我们走到一个串she的时候,我们不仅仅要看she是否是模式串,我们同时也要看它的后缀he,e是否是模式串,如果没有ne数组,我需要重新走he(0-2-3),e(0-1),如果存在ne数组,我可以直接走到he和e所在节点,同时如果最长后缀不在模式串里,其实ne是指向根节点(0)的,我们可以一步跳到根节点,就不必再一一找了,比如主串是son,此时我们走到了节点10,根据ne数组,我们可以直接直到son的后缀里不存在模式串,直接跳回了根节点。此时我们再明确一个点,就是ne数组存的最长后缀,一定是在模式串里出现过的,son的最长后缀是on,但是它在模式串里没有出现,所以ne数组就自然不会指向它,那么此时我再增添一个模式串n,那么节点10的ne数组会指向谁呢?如下图所示,
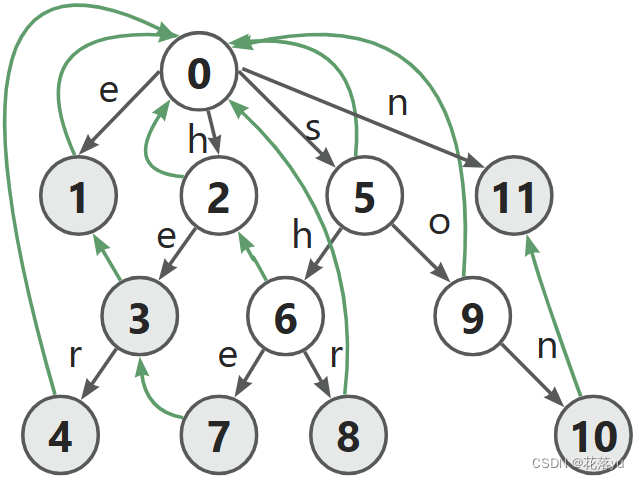
此时我们也就明确了ne数组的作用,即帮助我们同时进行多个模式串的匹配。
ch[u]数组
(1)ch[u][i]存节点u沿i走的转移边或者树边---------->为什么可以用同一个数组存两类边
(2)所指节点一定是当前节点的最短路---------->什么是当前节点的最短路and为什么要设置这个数组
(3)转移边指向当前节点的回跳边所指节点的儿子---------->为什么这么求
关于ch数组的问题,我们还是要看模式串匹配的过程,此时我们关注的是如何在ac自动机上进行指针的转移,在kmp里面,我们失配时根据next数组进行转移,那么这里我们又如何转移呢?
在代码里面k指针沿着主串走,i指针在ac自动机上移动,i指针的转移十分简单i = ch[i][string.charAt(k)-'a'];不需要判断是否失配,直接沿着ch数组走,那ch数组到底是干啥的?
ch数组存了两类边,树边和转移边,树边我们可以理解就是字典树上的边,假设我们的主串是sher,那么我们从根节点开始沿着树边走是没有问题的,相当于沿着某一个模式串去匹配,此时我们来到了节点7,下一个是字符是r,我们要沿着r走,可以看到此时已经没有沿着r走的树边了,我们从图里直接看的话,应该怎么走呢?我们有一个模式串her,那么主串里也有her,此时我可以走到节点4,那要怎么走呢?我们难道要回到根节点重新匹配吗?答案当然是不需要,我们在接着看这个例子,在节点7处失配,我们下一步是要沿着r走,she后面没有r了,我们可以试着看图,可能he后面有没有,e后面有没有,直到都没有才回到根节点,而这个过程就是转移边帮我们实现,我们怎么走到节点4,是不是节点7回跳边所指节点沿着r走的儿子,这里是不是也就说明了转移边是怎么构建的,同时也明白了转移边指向当前节点的最短路的意思,就是我不需要回退到根节点,而是一步到位,直接走到我该走的节点,现在我们再来看关于ch数组的那几个问题,
ch[u]数组:
(1)存节点u沿i走的转移边或者树边---------->为什么可以用同一个数组存两类边:因为失配的时候才会走转移边,而失配时不存在树边,也就是我们不存在一条边,既是树边又是转移边;这两个边的作用都是一样的。
(2)所指节点一定是当前节点的最短路---------->什么是当前节点的最短路and为什么要设置这个数组:当前节点的最短路是指我在当前节点失配时我应该走到哪个节点接着匹配;这个数组的作用指示了失配时如何走
(3)转移边指向当前节点的回跳边所指节点的儿子---------->为什么这么求:见加粗标记,其过程形成了三角形,如下图所示,