刷题系列——排序算法
参考:README - 十大经典排序算法
1)排序算法分为内部外部排序两种,这个之前并不了解,外部排序需要访问外存的这个就是指需要额外内存比如另一个list或者dict存储中间结果。
2)稳定性:排序后 2 个相等键值的顺序和排序之前它们的顺序相同,这点之前也不了解。
1. 冒泡排序:每次比较两个元素,随着遍历数组,最小的元素会浮到数组顶端。
1. 做完第一次遍历,最大的元素会到数组末端;每一次保证一个元素到了正确的位置,因此之后的遍历会逐渐缩短长度。
2. 实现: j和i的边界可以注意一下,当前是优化的写法。
def bubble_sort(lista):
num = len(lista)
for j in range(1, num):
for i in range(num - j):
if lista[i] > lista[i + 1]:
lista[i], lista[i + 1] = lista[i + 1], lista[i]
print(lista)
return lista
lista = [1,5,6,3,7,9,1]
bubble_sort(lista)3. 复杂度:最小O(n)是已经正序,最大O(n^2)是倒序,平均O(n^2),空间复杂度O(1),稳定,In-place。
2. 选择排序:每次遍历选择出最大/小元素放在尾/首,下一次选择次之。
1. 需要记录最大/小元素的索引,涉及到交换最大/小元素和首/尾元素。
2. 实现
def select_sort(lista):
num = len(lista)
for i in range(num - 1):
min_ele = i
for j in range(i + 1, num):
if lista[j] < lista[min_ele]:
min_ele = j
lista[i], lista[min_ele] = lista[min_ele], lista[i]
print(lista)
return lista3. 复杂度:最小O(n^2),最大O(n^2),平均O(n^2),空间复杂度O(1),不稳定,In-place。
4. 不稳定这个点需要注意,涉及到交换位置,所以相同大小元素本来的顺序会被打乱。
3. 插入排序:类比扑克牌
1. 保证一个已排列数组,插入的数据从后扫描已排列数组然后插入。
2. 把一个数组划分已排列和未排列待插入部分。
3. 实现:注意j的变化, j -= 1
def insert_sort(lista):
num = len(lista)
for i in range(1, num):
j = i
while j - 1 >= 0 and lista[j] < lista[j - 1]:
lista[j - 1], lista[j] = lista[j], lista[j - 1]
j -= 1
print(lista)4. 最小O(n),最大O(n^2),平均O(n^2),空间复杂度O(1),稳定,In-place。
4. 希尔排序:递减增量排序算法
1. 对插入排序的优化:将待排序部分划分为子序列,各自基本有序后,之后再插入排序。包含有归并的思路。
2. 子序列的划分方式是很重要的,如果连续几个数划分为一个子序列,对整体效率是无影响的,因此需要采用增量划分。
3. 增量是指划分的子序列的个数,增量递减直到为1,排序结束。
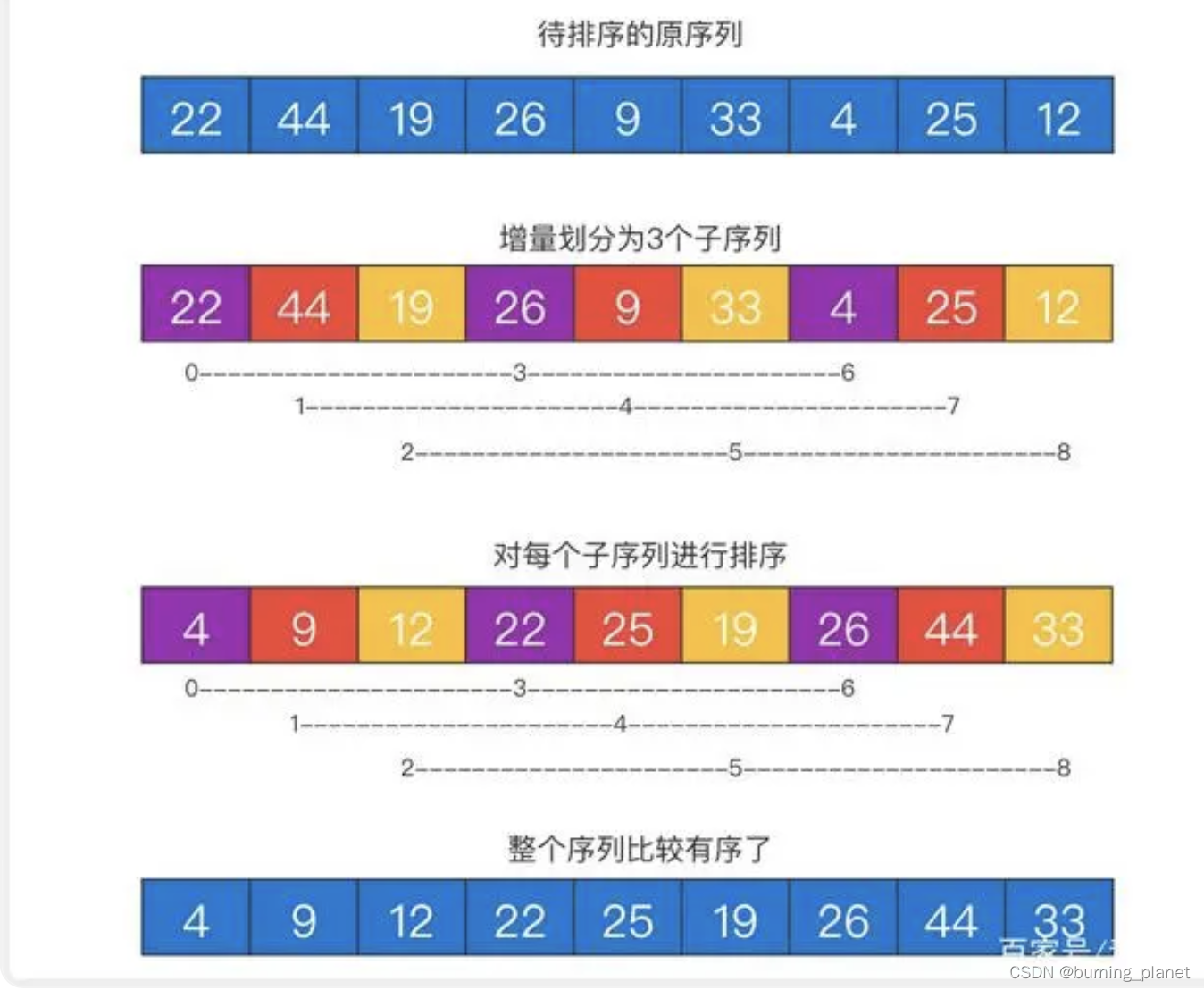
3. 不稳定因为子序列的排序会打乱原顺序。
4. 实现
def shell_sort(lista):
num = len(lista)
increment = num // 2
while increment > 0:
for i in range(increment, num):
idx = i
while idx >= increment and lista[idx] < lista[idx - increment]:
lista[idx], lista[idx - increment] = lista[idx - increment], lista[idx]
idx -= increment
increment //= 2
print(lista)5. 最小O(nlgn),其他不太确定,空间复杂度O(1),不稳定因为包含了插入排序,In-place。
5. 归并排序:分治法,需要额外空间
1. 分为自上而下的递归和自下而上的迭代,这点还不是很理解。
2. 参考:【Python入门算法23】排序入门:高效的归并排序 mergesort 的4种写法 - 知乎
3. 实现
def merge_sort(lista):
if len(lista) == 1:
return lista
idx = len(lista) // 2
left = merge_sort(lista[:idx])
right = merge_sort(lista[idx:])
merged = merge_1(left, right)
print(merged)
return merged
def merge(lista, listb):
merged = []
a, b = len(lista), len(listb)
i, j = 0, 0
while i < a and j < b:
if lista[i] < listb[j]:
merged.append(lista[i])
i += 1
else:
merged.append(listb[j])
j += 1
merged.extend(lista[i:])
merged.extend(listb[j:])
return merged
def merge_1(lista, listb):
if not lista:
return listb
if not listb:
return lista
if lista[0] < listb[0]:
return [lista[0]] + merge_1(lista[1:], listb)
else:
return [listb[0]] + merge_1(lista, listb[1:])6. 快速排序:采用分治法
1. 找到基准,基准左边比基准小,右边比基准大。
2. 对冒泡排序的改进,是内部排序的最优。
3. 实现
def quick_sort(lista, start, end):
if start >= end:
return lista[start:end]
pivot = lista[start]
left = start
right = end
while left < right:
while lista[right] >= pivot and left < right:
right -= 1
while lista[left] < pivot and left < right:
left += 1
lista[left], lista[right] = lista[right], lista[left]
lista[left] = pivot
quick_sort(lista, start, left-1)
quick_sort(lista, left+1, end)
print(lista)7. 堆排序:利用堆的数据结构,大顶堆用于升序排序和小顶堆用于降序排序
1. 构建堆,交换堆元素,重新构建堆
2. 参考:Python实现堆排序_堆排序python-CSDN博客
3. 实现
def heap_sort(lista):
idx = len(lista) // 2 - 1
for i in range(idx, -1, -1):
heapify(lista, i, len(lista) - 1)
for i in range(len(lista) - 1, -1, -1):
lista[i], lista[0] = lista[0], lista[i]
heapify(lista, 0, i - 1)
print(lista)
return lista
def heapify(lista, start, end):
root = start
left = root * 2 + 1
while left <= end:
if left + 1 <= end and lista[left] < lista[left + 1]:
left += 1
if lista[root] < lista[left]:
lista[root], lista[left] = lista[left], lista[root]
root = left
left = root * 2 + 1
else:
break 4. 平均复杂度Ο(nlogn),不稳定。
8. 计数排序:需要额外空间
1. 将输入的值转化为key存储在额外的空间中
2. 实现
def counting_sort(lista):
n = len(lista)
min_v = 222222222
max_v = 0
for ele in lista:
if ele > max_v:
max_v = ele
if ele < min_v:
min_v = ele
num = max_v - min_v + 1
listb = [0] * num
for i in lista:
listb[i - min_v] += 1
idx = 0
for i in range(max_v - min_v + 1):
for j in range(listb[i]):
lista[idx] = i + min_v
idx += 1
print(lista)
return lista3. 平均复杂度Ο(n+k),这个k的部分暂时不是很理解,空间复杂度O(k)。Out-place,不稳定。
9. 桶排序:计数排序的升级版
1. 包括分桶和合并两部分,对桶内的数据进行排序,再把桶内排序好的数据取出,又称为箱排序
2. 实现:里面调用了冒泡排序,调用快排时发现上面的代码有问题
def bucket_sort(lista):
listb = []
min_value = 222222222222
max_value = 0
for i in lista:
if i > max_value:
max_value = i
if i < min_value:
min_value = i
bucket_num = (max_value - min_value) // 3 + 1
buckets = [[] for i in range(bucket_num)]
for i in lista:
buckets[(i - min_value) // 3].append(i)
print(buckets)
for b in buckets:
b = bubble_sort(b)
print(b)
listb.extend(b)
print(listb)3. 是否稳定决定于桶内的排序算法。最快情况是数据被桶平分(n/k),具体复杂度决定于桶内的排序算法。
10. 基数排序:非比较型的排序算法,和桶排序思想类似
1. 除了对整数排序,也可以用于浮点数,字符串等。
2. 按位数分桶,分为MSD,LSD两种方法。
3. 实现
def radix_sort(lista):
max_value = max(lista)
place = 0
while max_value >= 10 ** (place):
place += 1
buckets = [[] for i in range(10)]
for i in range(place):
for j in lista:
ele = j % (10 ** (i + 1))
buckets[ele].append(j)
k = 0
for bucket in buckets:
if bucket:
lista[k] = bucket.pop(0)
k += 1
print(lista)4. 时间复杂度O(d(n+k)),d是最大值的位数,k是桶个数,n是队列长度。稳定,Out-place。
