当前位置：首页 > article >正文

合并两个有序链表[简单]

article 2024/9/20 9:32:16

优质博文：IT-BLOG-CN

一、题目

将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例 1：

输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

示例 2：
输入：l1 = [], l2 = []
输出：[]

示例 3：
输入：l1 = [], l2 = [0]
输出：[0]

::: warning
两个链表的节点数目范围是[0, 50]
-100 <= Node.val <= 100
l1和l2均按非递减顺序排列
:::

二、代码

【1】递归： 我们可以如下递归地定义两个链表里的merge操作（忽略边界情况，比如空链表等）：

也就是说，两个链表头部值较小的一个节点与剩下元素的merge操作结果合并。

我们直接将以上递归过程建模，同时需要考虑边界情况。如果l1或者l2一开始就是空链表，那么没有任何操作需要合并，所以我们只需要返回非空链表。否则，我们要判断l1和l2哪一个链表的头节点的值更小，然后递归地决定下一个添加到结果里的节点。如果两个链表有一个为空，递归结束。

class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        if (l1 == null) {
            return l2;
        } else if (l2 == null) {
            return l1;
        } else if (l1.val < l2.val) {
            l1.next = mergeTwoLists(l1.next, l2);
            return l1;
        } else {
            l2.next = mergeTwoLists(l1, l2.next);
            return l2;
        }
    }
}

时间复杂度： O(n+m)，其中n和m分别为两个链表的长度。因为每次调用递归都会去掉l1或者l2的头节点（直到至少有一个链表为空），函数mergeTwoList至多只会递归调用每个节点一次。因此，时间复杂度取决于合并后的链表长度，即O(n+m)。
空间复杂度： O(n+m)，其中n和m分别为两个链表的长度。递归调用mergeTwoLists函数时需要消耗栈空间，栈空间的大小取决于递归调用的深度。结束递归调用时mergeTwoLists函数最多调用n+m次，因此空间复杂度为O(n+m)。

【2】迭代： 我们可以用迭代的方法来实现上述算法。当l1和l2都不是空链表时，判断l1和l2哪一个链表的头节点的值更小，将较小值的节点添加到结果里，当一个节点被添加到结果里之后，将对应链表中的节点向后移一位。

首先，我们设定一个哨兵节点prehead ，这可以在最后让我们比较容易地返回合并后的链表。我们维护一个prev指针，我们需要做的是调整它的next指针。然后，我们重复以下过程，直到l1或者l2指向了null：如果l1当前节点的值小于等于l2，我们就把l1当前的节点接在prev节点的后面同时将l1指针往后移一位。否则，我们对l2做同样的操作。不管我们将哪一个元素接在了后面，我们都需要把prev向后移一位。

在循环终止的时候，l1和 l2 至多有一个是非空的。由于输入的两个链表都是有序的，所以不管哪个链表是非空的，它包含的所有元素都比前面已经合并链表中的所有元素都要大。这意味着我们只需要简单地将非空链表接在合并链表的后面，并返回合并链表即可。

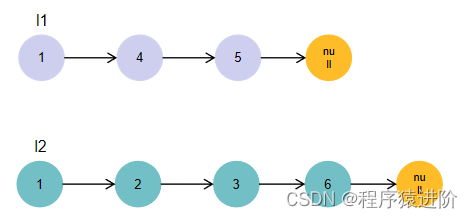
下图展示了1->4->5和1->2->3->6两个链表迭代合并的过程：

class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        ListNode prehead = new ListNode(-1);

        ListNode prev = prehead;
        while (l1 != null && l2 != null) {
            if (l1.val <= l2.val) {
                prev.next = l1;
                l1 = l1.next;
            } else {
                prev.next = l2;
                l2 = l2.next;
            }
            prev = prev.next;
        }

        // 合并后 l1 和 l2 最多只有一个还未被合并完，我们直接将链表末尾指向未合并完的链表即可
        prev.next = l1 == null ? l2 : l1;

        return prehead.next;
    }
}

时间复杂度： O(n+m)，其中n和m分别为两个链表的长度。因为每次循环迭代中，l1和l2只有一个元素会被放进合并链表中，因此while循环的次数不会超过两个链表的长度之和。所有其他操作的时间复杂度都是常数级别的，因此总的时间复杂度为O(n+m)。
空间复杂度： O(1)。我们只需要常数的空间存放若干变量。