当前位置：首页 > article >正文

【初阶解法-数据结构】包含min函数的栈(代码+图示)

article 2024/9/19 9:40:29

【数据结构】刷题-包含min函数的栈(代码+图示)-初阶解法

文章目录

【数据结构】刷题-包含min函数的栈(代码+图示)-初阶解法
- 题目
- 提炼题目要求
- 分析题目
- 总结思路
- 代码
- 时间/空间复杂度
- 进阶版

题目

定义栈的数据结构，请在该类型中实现一个能够得到栈中所含最小元素的 min 函数，输入操作时保证 pop、top 和 min 函数操作时，栈中一定有元素。

此栈包含的方法有：

push(value):将value压入栈中

pop():弹出栈顶元素

top():获取栈顶元素

min():获取栈中最小元素

数据范围：操作数量满足 0≤n≤300 ，输入的元素满足 ∣val∣≤10000

栈的各个操作的时间复杂度是 O(1) ，空间复杂度是O*(n)

提炼题目要求

题目核心要求

实现push(value),pop(),top(),min()函数
要求各个函数的时间复杂度均为O(1)
空间复杂度为O(n)

分析题目

解决这类问题的关键是设计一个能够在O(1)时间内完成 push、pop、top 和 min 操作的数据结构。通常，我们会考虑 使用辅助栈或其他数据结构来维护额外的信息。

当我遇到这类问题时，我会考虑以下几个步骤：

使用辅助栈：
- 我通常会考虑使用一个辅助栈来保存额外的信息，比如最小值。
- 辅助栈可以在主栈的每个状态下都保存一些额外的信息，以便在O(1)时间内支持 min 操作。
考虑特殊情况：
- 考虑空栈的情况，并确保代码对空栈的处理是正确的。
保持同步：
- 在使用辅助栈或其他数据结构时，确保主栈和辅助数据结构之间保持同步，以防止出现不一致的情况。
复杂度分析：
- 在实现解决方案后，分析代码的时间复杂度和空间复杂度，确保它们满足问题的要求。

举例来说，如果题目要求实现一个支持O(1)时间复杂度的 min 操作的栈，我可能会考虑使用辅助栈来保存每个状态下的最小值。在 push 操作中，我会在辅助栈中更新最小值；在 pop 操作中，我会同时弹出主栈和辅助栈的栈顶元素。这样就能够保持O(1)时间复杂度的 min 操作。

总结思路

下面是一种使用辅助栈的简单实现思路：初阶

主栈 s1 用于正常的栈操作。
辅助栈 s2 用于存储每个状态下的最小值。

在 push 操作时：

将元素压入主栈 s1。
检查辅助栈 s2 是否为空，或者新元素是否小于等于辅助栈的栈顶元素。如果是，将新元素也压入辅助栈 s2。否则，重复压入辅助栈的栈顶元素。

在 pop 操作时：

分别从主栈 s1 和辅助栈 s2 弹出栈顶元素。

在 min 操作时：

直接返回辅助栈 s2 的栈顶元素。

NOTE : 这样，辅助栈 s2 中的栈顶元素始终对应于主栈 s1 的当前最小值，而且由于每次 push 和 pop 操作都会同时更新两个栈，保持了两个栈的同步。这样，min 操作的时间复杂度是 O(1)。

如果对于push操作中的重复压入辅助栈的栈顶元素感到困惑，我将详细解释这背后的原因。

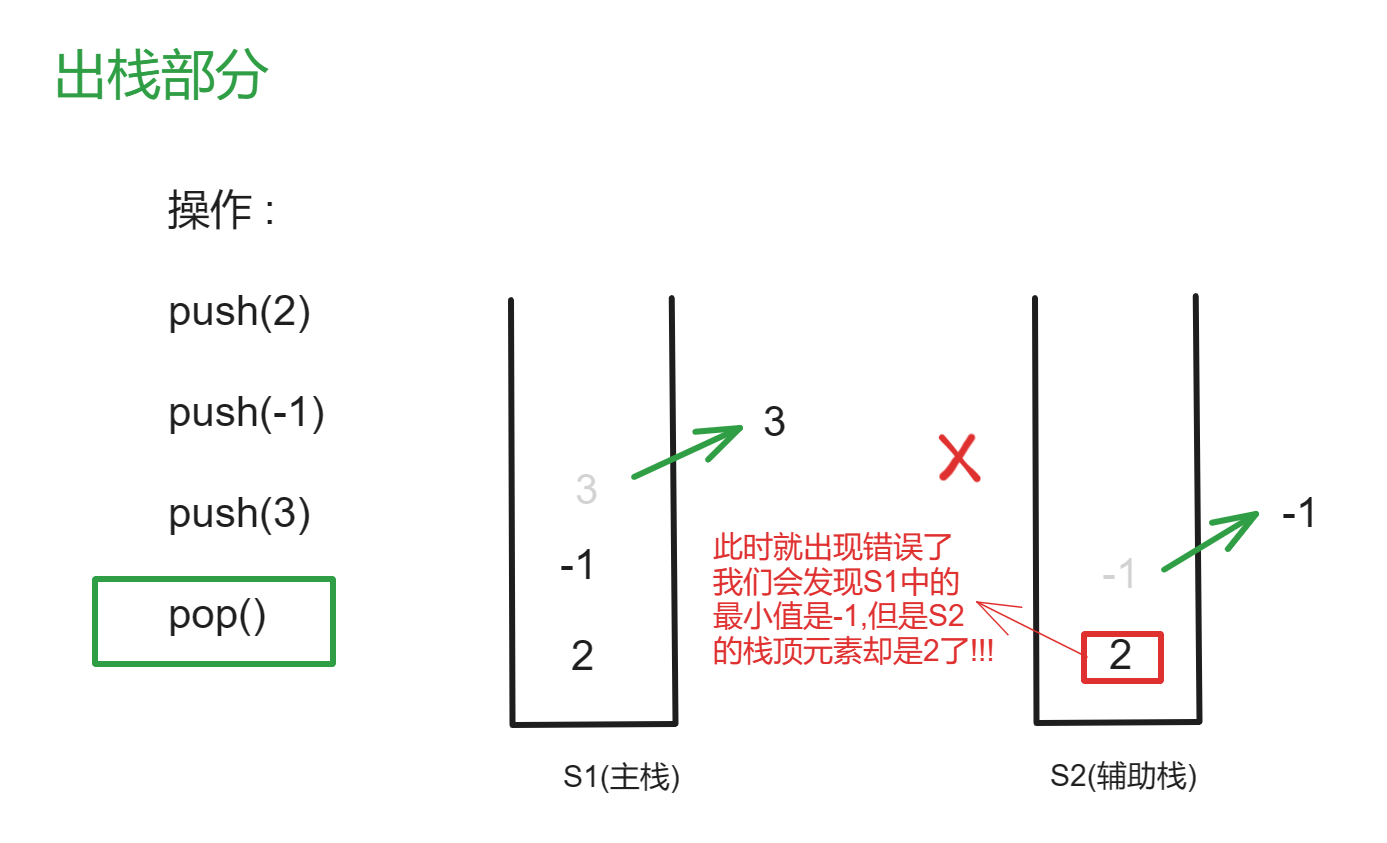
当我们仅仅在push操作中实时监控辅助栈s2的栈顶元素是否一直保持是所有元素中的最小值时，这只是解决了问题的一半。因为栈中元素的变动不仅仅是由push操作引起的，我们还需要考虑pop操作。在弹出元素的同时，主栈s1中的元素也发生了变化。因此，为了确保s2能够实时监控到pop操作，我们必须同时在主栈s1进行pop操作的时候，保证辅助栈s2也要同时更新以进行pop操作。那么问题来了，如何在s2中保证有元素可以弹出，并且不会改变栈顶元素一直是最小值呢？
- 解决这个问题的方法是，在入栈push的时候，如果待插入的元素比最小值大，我们就将当前最小值重复入栈。这样就保证了每当主栈s1入栈一个元素时，辅助栈s2也会入栈一个元素。这种做法的好处在于，之后无论何时进行出栈pop操作，我们都能够确保s2中有元素可以弹出。而且，一旦成功弹出元素，s2的栈顶元素仍然保持是最小值！
- 如下图演示

(同步)正常的出栈操作

(未同步)异常的出栈操作

代码

import java.util.*;
import java.util.Stack;


/*
含有min函数的栈

这个题目需要我们自己实现栈的基本的结构
 */

public class Solution{

    //这个栈1是我们的主要的栈
    Stack<Integer> stack1 = new Stack<>();

//这个栈2 是我们专门用来保存最小值的栈
    Stack<Integer> stack2 = new Stack<>();

    public void push(int node) {

        //准备一个辅助栈,这个栈必须在push方法中,因为这样我们就可以直接就保证min函数里面的栈中保存的一定是最小的值
        //所以我们就只需要在插入元素的时候就进行筛查
        stack1.push(node);
       
        if(stack2.empty()||node<stack2.peek()){
            stack2.push(node);
        }else{
            stack2.push(stack2.peek());
        }
    }

    public void pop() {
        stack1.pop();
        stack2.pop();
    }

    public int top() {
        return stack1.peek();

    }

    public int min() {
        return stack2.peek();
    }
}

时间/空间复杂度

时间复杂度分析

push(int node):

stack1.push(node)：将元素推入主栈 stack1，O(1)。
判断并更新最小值：
- 如果 stack2 为空，或者新元素 node 小于 stack2 的栈顶元素，执行 stack2.push(node)，O(1)。
- 否则，执行 stack2.push(stack2.peek())，O(1)。
因此，整体的时间复杂度为 O(1)。

pop():