POJ 3233 Matrix Power Series 动态规划(矩阵的幂)
一、题目大意
给出一个矩阵A,
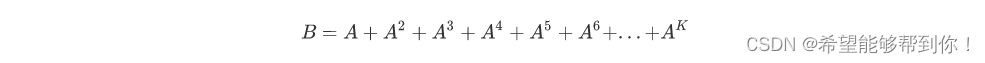
输出矩阵B的每一项对M取余数的值。
二、解题思路
以二维矩阵为例,首先计算K=2的情况,我们设结果矩阵为B
有如下表达式

那么不难看出,需要的矩阵其实就是以下的两个矩阵相乘后的左上角的N*N个

然后我们再来考虑K=3的情况,我们设结果矩阵为C

我们来考虑如何把C表示成矩阵B和A相乘的状态。
不难看出C矩阵就是以下两个矩阵相乘后的N*N的左上角

也是如下矩阵的左上角

综上,我们发现计算B和C时,乘号右边的矩阵是相同的,只是我们需要保证前N排的后N列必须始终为A[0][0]..A[0][N-1],A[1][0]..A[1][N-1],...
保留那些值我们可以通过给右边的矩阵右下角放置零矩阵即可。
那么最终题目的答案可以表示成下的表达式。
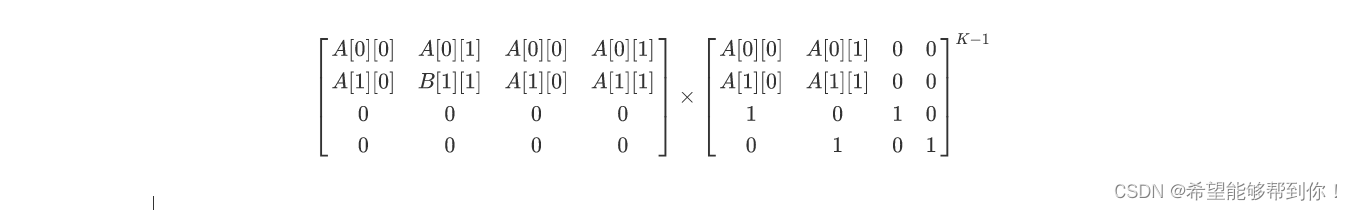
三、代码
#include <iostream>
#include <vector>
using namespace std;
typedef vector<int> vec;
typedef vector<vec> mat;
int M;
mat mul(mat &A, mat &B)
{
mat C = mat(A.size(), vec(B[0].size()));
for (int i = 0; i < A.size(); i++)
{
for (int j = 0; j < B[0].size(); j++)
{
for (int k = 0; k < B.size(); k++)
{
C[i][j] = (C[i][j] + A[i][k] * B[k][j]) % M;
}
}
}
return C;
}
mat pow(mat &A, int N)
{
mat B = mat(A.size(), vec(A[0].size()));
for (int i = 0; i < B.size(); i++)
{
B[i][i] = 1;
}
while (N > 0)
{
if (N & 1)
{
B = mul(B, A);
}
A = mul(A, A);
N >>= 1;
}
return B;
}
void solve()
{
int N, K;
scanf("%d%d%d", &N, &K, &M);
mat A = mat(2 * N, vec(2 * N));
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
scanf("%d", &A[i][j]);
}
}
for (int i = 0; i < N; i++)
{
A[i + N][i] = 1;
A[i + N][i + N] = 1;
}
mat B = mat(2 * N, vec(2 * N));
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
B[i][j] = A[i][j];
B[i][j + N] = A[i][j];
}
}
A = pow(A, K - 1);
A = mul(B, A);
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
printf("%d%c", A[i][j] % M, j + 1 == N ? '\n' : ' ');
}
}
}
int main()
{
solve();
return 0;
}