当前位置：首页 > article >正文

NTT入门开拓者的卓识

article 2024/11/17 4:24:24

link

大意：

给定一个长度为n的数组a
$\forall i \in [1,n]$ ，求[1,n]的k阶子段和

我们定义k阶子段和如下：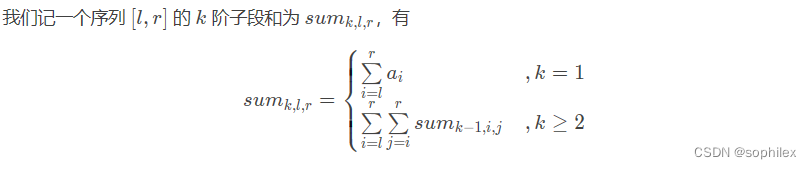

思路：

这个k阶字段和，就是在k-1阶的基础上，再讲所有k-1阶的子段和都相加得到k阶子段和

k是很大的，所以我们很自然地想到按每一个数字的贡献来求总和:

一阶子段和[l,r]就是区间前缀和，ai有贡献当且仅当i在区间内部，贡献为1

二阶子段和[l,r]就是在找l',r',使得l<=l'<=i<=r'<=r,ai的贡献就是这样的l',r'的对数

以此类推，我们的k阶字段和就是在区间[l,r]内找到满足条件的l',r',使得有k个区间包含它们对应区间。换句话说，是要在区间内找到k-1对包含i的子区间，并且它们是嵌套的关系（可以相等）

lk=1⩽lk−1⩽lk−2⩽…⩽l1⩽i⩽r1⩽…⩽rk−1⩽rk

不难发现区间的左右边界互不影响。

所以我们考虑一下在一个长度为i的区间里放k-1个数的方案数，其中这k-1个数可以取等。这就是一个经典的隔板法，方案数就是C(i+k-2,k-1)。或者我们也可以这样考虑：
枚举出现过的数字的个数x，然后就是将k-1个数分成x块的方案数

就是 $\sum_{i=1}^{x}\binom{x}{i}\binom{k-1-1}{i-1}$ ,这可以转化为一个范德蒙德卷积（i=0时值为0），化简之后就是上式。

这其实就是在i点左侧找k-1个数的方案数，那么右侧找k-1个数也是同理

所以如果当前区间右界是r的话，我们的答案就是

$ans_r=\sum_{i=1}^{r}a_i*\binom{i+k-2}{k-1}\binom{r-i+k-1}{k-1}$

这个复杂度是n^2的

我们考虑优化：

不难发现，i+k-2+r-i+k-1是一个常值，这也就意味着我们可以使用ntt优化

令 $p(i)=\binom{i+k-2}{k-1}$

则原式化简如下： $ans_r=\sum_{i=1}^{r}a_i*p(i+k-2)*p(r-i+k-1)$

我们令 $f(i)=a_i*p(i+k-2),g(i)=p(i+k-1)$

则原式化简如下: $ans_r=\sum_{i=1}^{r}f(i)*g(r-i)$

这样就是一个标准的卷积了

另外，组合数预处理的话，因为k很大，而且我们只用求以k-1为底的组合数，所以可以递推来求组合数

code

#include<bits/stdc++.h>
using namespace std;
#define ll long long
//#define int ll
#define endl '\n'
const ll N=1e5+10;
const ll mod=998244353;
ll G=3,invG;
ll n,k;
ll mas[N];
ll f[N<<2],g[N<<2],inv[N];
ll limit,L;
ll R[N<<2];
ll Invv;//inv(limit)
ll ksm(ll x,ll y)
{
    ll ans=1;
    while(y)
    {
        if(y&1) ans=ans*x%mod;
        x=x*x%mod;
        y>>=1;
    }
    return ans;
}
ll invv(ll x)
{
    return ksm(x,mod-2);
}
void init(ll x)
{
    invG=invv(G);
    limit=1,L=0;
    while(limit<=x)
    {
        limit<<=1;
        L++;
    }
    for(ll i=0;i<limit;++i) R[i]=(R[i>>1]>>1)|((i&1)<<(L-1));
        Invv=invv(limit);
}
void ntt(ll *a,ll len,ll ty)
{

    for(int i=0;i<len;++i) if(R[i]>i) swap(a[i],a[R[i]]);
    for(int k=1;k<len;k<<=1)
    {
        ll d=ksm((ty==1)?G:invG,(mod-1)/(k<<1));
        for(int i=0;i<len;i+=(k<<1))
        {
            for(int j=i,g=1;j<i+k;++j,g=(g*d)%mod)
            {
                ll Nx=a[j],Ny=((a[j+k]*g)%mod);
                a[j]=(Nx+Ny)%mod;
                a[j+k]=((Nx-Ny)%mod+mod)%mod;
            }
        }
    }
    if(ty!=1)
    {
        for(int i=0;i<=len;++i) a[i]=a[i]*Invv%mod;
    }
}
void cinit()
{
    inv[1]=1;
    for(int i=2;i<=n;++i) inv[i]=(mod-mod/i)*inv[mod%i]%mod;
    g[0]=1;
    for(int i=1;i<=n;++i) g[i]=g[i-1]*(i+k-1)%mod*inv[i]%mod;
    for(int i=1;i<=n;++i) f[i]=mas[i]*g[i-1]%mod;
}
void solve()
{
    cin>>n>>k;
    for(int i=1;i<=n;++i) cin>>mas[i];
    cinit();
    init(n+n);

    ntt(f,limit,1);ntt(g,limit,1);
    for(int i=0;i<=limit;++i) f[i]=f[i]*g[i]%mod;

    ntt(f,limit,0);
    for(int i=1;i<=n;++i) cout<<f[i]<<" ";
    cout<<endl;

}
signed main()
{
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    solve();
    return 0;
}

查看全文

http://www.kler.cn/a/15954.html