二叉平衡树

一直想深入的研究一下，并手写平衡二叉树的插入、删除代码。

二叉树是动态查找的典范，但在极限情况下，二叉树的查找效果等同于链表，而平衡二叉树可以完美的达到${\log }_{2}n$。

AVL简称平衡二叉树，缩写为BBST，由苏联数学家 Adelse-Velskil 和 Landis 在 1962 年提出。

例子：

将17，9，2，12，14，26，33，15，40，23，25一次插入到一棵初始化为空的AVL树中，画出该二叉平衡树。

解：过程和结果如下图所示。

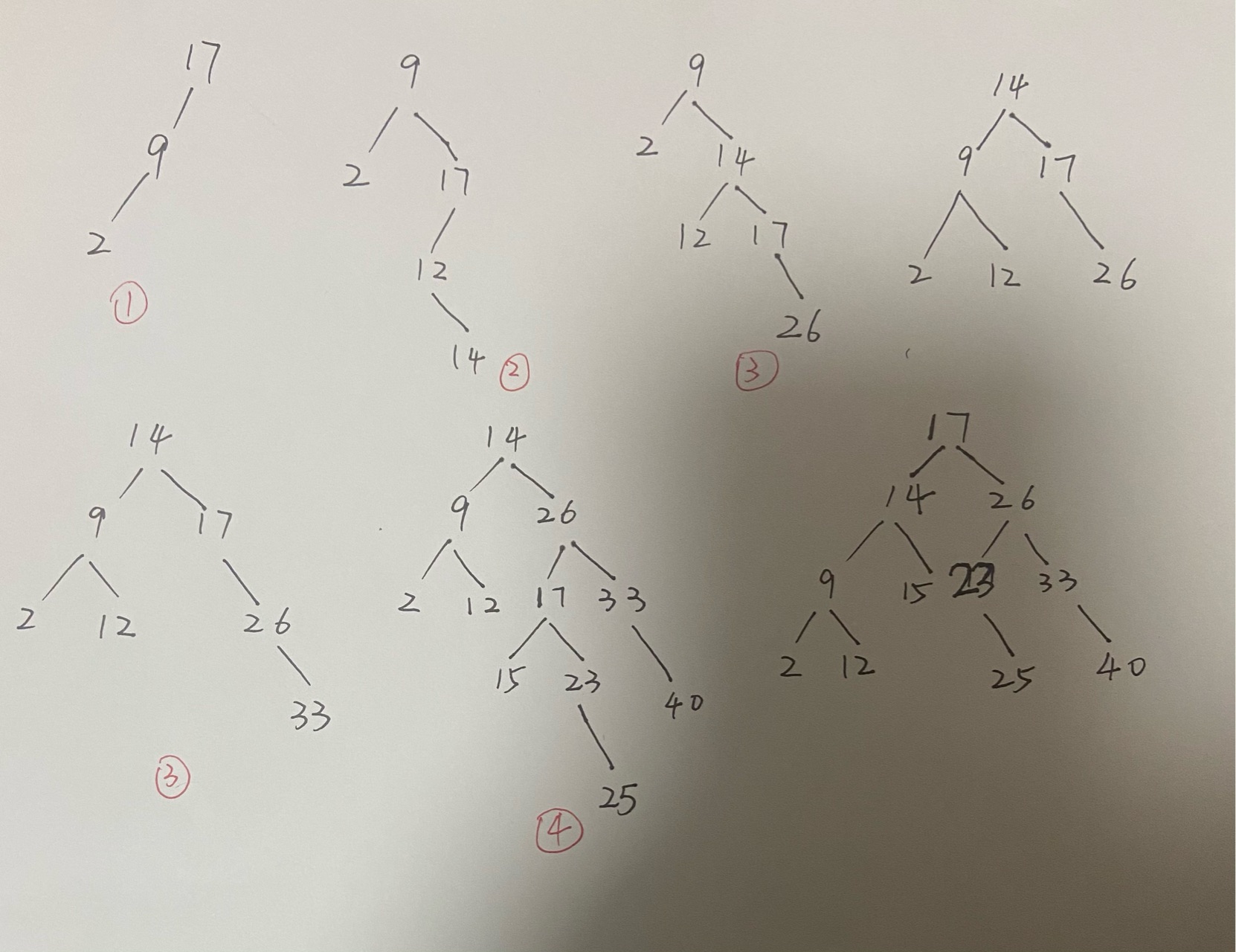
所谓平衡二叉树，就是指二叉树的左、右子树的深度差不超过2。每当超过时，需要对二叉树的失衡节点进行平衡。

BBST用两个整数来表示左右子树的深度，前面一个表示左子树的层数，右边一个代表右子树的层数。

调整时，首先需要找到要平衡的节点。找到调整节点后，处理的方法有4种：

上图中圆标号1的是左-左结构，标号2的是左-右结构，标号3的是右-右，标号4的是右-左结构，这4种结构的处理方式各有不同。

1. 左-左结构，即(2，1)结构

中间节点当作父节点，最上面的节点当作右节点，最下边节点当作左节点

2. 左-右结构，即(2，-1)结构

最下面节点当作父节点，父节点当作右节点，中间节点当作左节点

3. 右-右结构，即(-2，-1)结构

中间节点当作父节点，最上面的节点当作左节点，最下边节点当作右节点

4. 右-左结构，即(-2，1)结构

最下面节点当作父节点，最上面节点当作左节点，中间节点当作右节点

编程中，计算左、右子树深度的代码如下：

int deep(BBST* b) {
	if (b == 0)
	{
		return 0;
	}

	int ld =  deep(b->lchild);
		
	int rd = deep(b->rchild) ;
	
	return ld > rd ? ld + 1 : rd + 1;
}

有了上面的理论和编程基础，我们可以慢慢的调试并手动写出平衡二叉树的插入代码：

int BBSTree::insert(ELEMENT* e) {
	if (mTree == 0)
	{
		mTree = newnode(e);
		mSize = 1;
		return 1;
	}

	BBST* t = mTree;

	BBST* tc = 0;
	Stack s;

	ELEMENT elem;

	while (1) {
		if (e->e == t->data.e) {
			return 0;
		}
		else if (e->e > t->data.e)
		{
			if (t->rchild == 0)
			{
				tc = newnode(e);
				tc->parent = t;
				t->rchild = tc;
				mSize++;
				break;
			}
			else {			
				elem.e = (unsigned long long)t;
				s.push((ELEMENT*)&elem);

				t = t->rchild;				
			}
		}
		else {
			if (t->lchild == 0)
			{
				tc = newnode(e);
				tc->parent = t;

				t->lchild = tc;
				mSize++;
				break;
			}
			else {
				elem.e = (unsigned long long)t;
				s.push((ELEMENT*)&elem);

				t = t->lchild;		
			}
		}
	}

	while (s.isEmpty() == 0) {

		s.pop(&elem);
		BBST* b = (BBST*)elem.e;
		b->ld = deep(b->lchild);
		b->rd = deep(b->rchild);

		t->ld = deep(t->lchild);
		t->rd = deep(t->rchild);

		int high_diff = b->ld - b->rd;
		int low_diff = t->ld - t->rd;
		if(high_diff == 2 && low_diff == 1)
		{
			BBST* f = (BBST*)b->parent;
			if (f&&f->lchild == b)
			{
				f->lchild = t;
			}
			else if (f&&f->rchild == b)
			{
				f->rchild = t;
			}
			BBST* old_tr = t->rchild;
			t->rchild = b;
			b->parent = t;

			t->parent = f;
			b->rchild = old_tr;
		}
		else if (high_diff == 2 && low_diff == -1)
		{
			BBST* f = (BBST*)b->parent;
			if (f->lchild == b)
			{
				f->lchild = tc;
			}
			else if (f->rchild == b)
			{
				f->rchild = tc;
			}

			BBST* ltmp = t;
			while (ltmp->rchild)
			{
				ltmp = ltmp->rchild;
			}
			tc->lchild->parent = ltmp->rchild;
			ltmp->rchild = tc->lchild;

			BBST* rtmp = b;
			while (rtmp->lchild)
			{
				rtmp = rtmp->lchild;
			}
			tc->rchild->parent = rtmp->lchild;
			rtmp->lchild = tc->rchild;

			tc->rchild = b;
			tc->lchild = t;
			b->parent = tc;
			t->parent = tc;

			tc->parent = f;
		}
		else if (high_diff == -2 && low_diff == 1)
		{
			BBST* f = (BBST*)b->parent;
			if (f&&f->lchild == b)
			{
				f->lchild = tc;
			}
			else if (f&&f->rchild == b)
			{
				f->rchild = tc;
			}

			BBST* rtmp = b;
			while (rtmp && rtmp->rchild)
			{
				rtmp = rtmp->rchild;
			}
			tc->lchild->parent = rtmp->rchild;
			rtmp->rchild = tc->lchild;

			BBST* ltmp = t;
			while (ltmp && ltmp->lchild)
			{
				ltmp = ltmp->lchild;
			}
			tc->rchild->parent = ltmp->lchild;
			ltmp->lchild = tc->rchild;
			
			tc->rchild = t;
			tc->lchild = b;
			b->parent = tc;
			t->parent = tc;

			tc->parent = f;
		}
		else if (high_diff == -2 && low_diff == -1)
		{
			BBST* f = (BBST*)b->parent;
			if (f && f->lchild == b)
			{
				f->lchild = t;
			}
			else if (f && f->rchild == b)
			{
				f->rchild = t;
			}
			BBST* old_tl = t->lchild;
			t->lchild = b;
			b->parent = t;

			t->parent = f;
			b->lchild = old_tl;
		}
		tc = t;
		t = b;
	}

	return 0;
}

完整代码地址：
https://github.com/satadriver/dataStruct