【二分答案法】寻找峰值

题目：162. 寻找峰值 - 力扣（LeetCode）

题目描述：

题目分析：

        （1）据题知，索引-1、索引n（n为数组长度）处的元素都默认为无穷小，我们可以在一开始特判一些简单情况：当数组长度等于1时，直接返回0；当索引0处的元素大于索引1处的元素时，直接返回0；当索引n - 1处的元素大于索引n-2处的元素时，返回n - 1。

        （2）如果给定的数组不满足特判条件，用折线来描述这个数组的升降，一定能找到一个峰值元素，如下图所示。

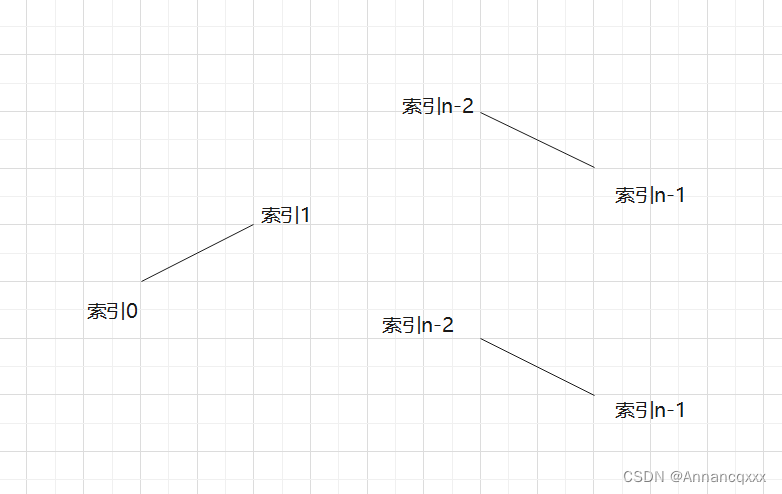
        索引0到索引1是上升趋势，索引n-2到索引n-1是下降趋势，由于数组不存在重复元素，所以无论你怎么拼接这条折线，中间一定有一个峰值元素。

        （3）假设我们二分到一个元素nums[m]，有三种情况：1、nums[m]就是峰值元素，更新答案，退出循环；2、nums[m-1] > nums[m]，这里呈下降趋势，而索引0到索引1是上升趋势，所以在0 到 m - 1这个区间肯定有一个峰值元素，right = m - 1往左侧二分；3、nums[m+1] > nums[m]，这里呈上升趋势，而索引n - 2到索引n - 1是下降趋势，所以在m + 1 到 n - 2这个区间肯定有一个峰值元素，left = m + 1往右侧二分。

Code：

class Solution {
    public int findPeakElement(int[] nums) {
        int n = nums.length;
        
        //数组中只有一个元素，直接返回0
        if(n == 1)
        return 0;
        
        //索引0处的元素满足要求，返回0
        if(nums[0] > nums[1])
        return 0;
        
        //索引n - 1处的元素满足要求，返回n - 1
        if(nums[n - 1] > nums[n - 2])
        return n - 1;

        int left = 1,right = n - 2;
        int ans = 0;
        while(left <= right){
            int m = left + (right - left) / 2;
            
            //nums[m-1] > nums[m]，这里是下降趋势
            //那么答案一定在左侧，往左侧二分
            if(nums[m - 1] > nums[m]){
                right = m - 1;
            }
            //nums[m+1] > nums[m]，这里是上升趋势
            //答案一定在右侧，往右侧二分
            else if(nums[m + 1] > nums[m]){
                left = left + 1;
            }else{
                //nums[m+1]和nums[m-1]都不大于nums[m]
                //那么nums[m]就是峰值元素
                ans = m;
                break;
            }
        }
        return ans;
    }
}