当前位置： 首页 > article >正文

WebGL笔记：矩阵旋转运算的原理和实现

article 2024/11/13 21:26:07

矩阵

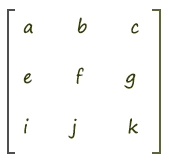
  • 矩阵（Matrix）是一个按照矩形纵横排列的复数集合
    • 矩阵就像一个矩形的阵盘，通过其中纵横排列的元素
    • 我们可以摆出不同功能的阵法，比如位移矩阵、旋转矩阵、缩放矩阵 …
    • 在矩阵中的每一行，或者每一列数字构成的集合，可以视之为向量


  • 关于复数 z = a + bi
    • 实数: b = 0
      • 有理数: 整数和分数
      • 无理数: eg: 圆周率 π， sqrt(2)
    • 虚数: b != 0

向量

  • 向量，又叫矢量，它是一个用于表示方向和量的对象
  • 在webgl 里的向量有1维向量、2维向量、3维向量和4维向量
    • 1维向量中有1个数字，对应的是单轴坐标系里的点位
    • 2维向量中有2个数字，对应的是2维坐标系里的点位
    • 3维向量中有3个数字，对应的是3维坐标系里的点位
    • 4维向量中有4个数字，对应的是3维坐标系里的点位，外加一个附加数据，至于这个数据是什么，要看我们的项目需求

矩阵和向量的乘法

  • 矩阵和向量的乘法图


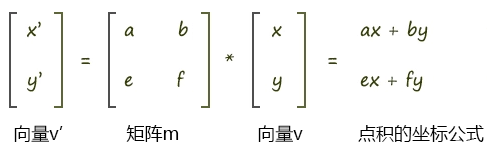
  • 矩阵乘以向量时，向量是几维的，那矩阵中就应该有几个向量
  • 如上图向量v 是2维的，那么矩阵中就有2组向量，这两组向量可以是横着的两组向量，也可以是竖着的两组向量
    • 横着的两组向量是：向量(a,b)、向量(e,f)
    • 竖着的两组向量是：向量(a,e)、向量(b,f)
    • 横着的两组遵循的规则是行主序，即将矩阵中的一行数据视之为一个向量
    • 竖着的两组遵循的规则是列主序，即将矩阵中的一列数据视之为一个向量
  • 我们是使用行主序，还是列主序，这就得看规则的定制者
  • 在webgl 里，矩阵元素的排列规则是列主序
  • 数学中常用的写法是行主序，所以我们接下来就用行主序例子
    • 矩阵和向量相乘的规则就是让矩阵中的每个向量和向量v相乘。
    • 向量和向量相乘，就是在求向量的点积，其结果是一个实数，而不再是向量
    • 比如上图中，向量(a,b)乘以向量v(x,y)的结果是：
      a * x + b * y
  • 因为a、b、x、y都是实数，所以其结果也是实数
  • 上图中，矩阵m乘以向量v 会得到两个结果，即ax+by和ex+fy
  • 这两个结果会构成一个新的向量v’(x’,y’)
    x' = a * x + b * y
y' = e * x + f * y
  • 这时我们可以将其和数学里的旋转公式做一下比较
  • 点A(ax,ay)围绕z轴旋β度,其旋转后的位置是点B(bx,by)，则：
    bx = cosβ * ax - sinβ * ay
by = sinβ * ax + cosβ * ay
  • 对比上面的两组公式，试想一下
  • 向量v是可以当成一个点位
  • 那我现在就让向量v代表的位置，就是点A的位置。
  • 那么矩阵m乘以向量v，是不是可以让向量v代表的这个点位旋转β度呢？
  • 如果可以，那么矩阵里的元素应该满足什么条件呢？
  • 满足以下条件即可
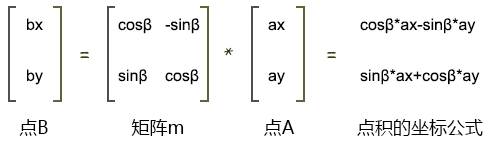
    a = cosβ
b = -sinβ
e = sinβ
f = cosβ
  • 这样，用矩阵乘以向量的方法得到的旋转结果和用数学公式得到的结果就是一样的，即;
    a * x + b * y = cosβ * ax - sinβ * ay
e * x + f * y = sinβ  *ax + cosβ * ay


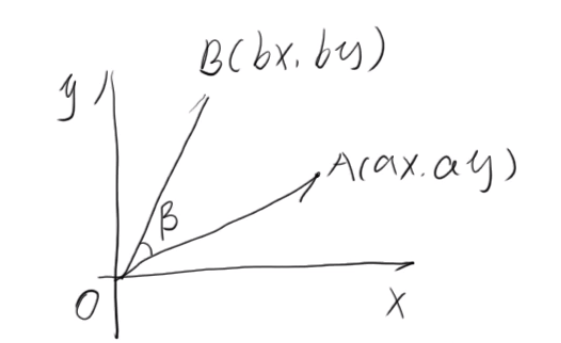
  • 最终我们就可以用矩阵乘以向量的方式让点p旋转β度
  • 也就是说，可以用矩阵乘以向量的方式求向量OA旋转了 β \beta β° 的位置


### 在着色器中书写矩阵

1 ） 核心代码

  • 在着色器中建立矩阵对象
    • mat2 是二维矩阵对象
<script id="vertexShader" type="x-shader/x-vertex">
    attribute vec4 a_Position;
    float angle = radians(40.0);
    float sinB = sin(angle);
    float cosB = cos(angle);
    mat2 m2 = mat2(
      cosB, sinB,
      -sinB, cosB
    );
    void main() {
      gl_Position = vec4(
        m2 * vec2(a_Position),
        a_Position.z, a_Position.w
      );
    }
</script>

2 ）完整代码

<canvas id="canvas"></canvas>
<script id="vertexShader" type="x-shader/x-vertex">
  attribute vec4 a_Position;
  float angle = radians(40.0);
  float cosB = cos(angle);
  float sinB = sin(angle);
  // 列主序
  mat2 m2 = mat2(
    cosB, sinB,
    -sinB, cosB
  );
  void main() {
    gl_Position = vec4(
      m2 * vec2(a_Position),
      a_Position.z, a_Position.w
    );
  }
</script>
<script id="fragmentShader" type="x-shader/x-fragment">
  void main() {
    gl_FragColor = vec4(1.0, 1.0, 0.0, 1.0);
  }
</script>
<script type="module">
  import { initShaders } from './utils.js';

  const canvas = document.getElementById('canvas');
  canvas.width = window.innerWidth;
  canvas.height = window.innerHeight;
  const gl = canvas.getContext('webgl');

  const vsSource = document.getElementById('vertexShader').innerText;
  const fsSource = document.getElementById('fragmentShader').innerText;
  initShaders(gl, vsSource, fsSource);

  const vertices = new Float32Array([
    0.0, 0.1,
    -0.1, -0.1,
    0.1, -0.1
  ])

  const vertexBuffer = gl.createBuffer();
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer);
  gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STATIC_DRAW);
  const a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0);
  gl.enableVertexAttribArray(a_Position);
  gl.clearColor(0.0, 0.0, 0.0, 1.0);
  gl.clear(gl.COLOR_BUFFER_BIT);
  gl.drawArrays(gl.TRIANGLES, 0, 3);
</script>

用js建立矩阵对象并传递给着色器

1 ）核心代码

  • 在顶点着色器中建立uniform变量

    <script id="vertexShader" type="x-shader/x-vertex">
    attribute vec4 a_Position;
    uniform mat2 u_Matrix;
    void main() {
      gl_Position = vec4(
        u_Matrix * vec2(a_Position),
        a_Position.z, a_Position.w
      );
    }
</script>

  • 获取并修改uniform 变量

    const u_Matrix = gl.getUniformLocation(gl.program, 'u_Matrix');
let angle = 0.2;
const [sinB, cosB] = [Math.sin(angle), Math.cos(angle)];
const matrix = [
    cosB, sinB,
    -sinB, cosB
];
gl.uniformMatrix2fv(u_Matrix, false, matrix);

  • 后面我们也可以在其中添加动画

    const u_Matrix = gl.getUniformLocation(gl.program, 'u_Matrix');
let angle = 0.2;
!(function animate() {
    angle += 0.02;
    const [sinB, cosB] = [Math.sin(angle), Math.cos(angle)];
    const matrix = [
        cosB, sinB,
        -sinB, cosB
    ];
    gl.uniformMatrix2fv(u_Matrix, false, matrix);
    gl.clear(gl.COLOR_BUFFER_BIT);
    gl.drawArrays(gl.TRIANGLES, 0, 3);
    requestAnimationFrame(animate)
})()

2 ）完整代码

<canvas id="canvas"></canvas>
<script id="vertexShader" type="x-shader/x-vertex">
  attribute vec4 a_Position;
  // 列主序
  uniform mat2 u_Matrix;
  void main() {
    gl_Position = vec4(
      u_Matrix * vec2(a_Position),
      a_Position.z,a_Position.w
    );
  }
</script>
<script id="fragmentShader" type="x-shader/x-fragment">
  void main() {
    gl_FragColor = vec4(1.0, 1.0, 0.0, 1.0);
  }
</script>

<script type="module">
  import { initShaders } from './utils.js';

  const canvas = document.getElementById('canvas');
  canvas.width = window.innerWidth;
  canvas.height = window.innerHeight;
  const gl = canvas.getContext('webgl');

  const vsSource = document.getElementById('vertexShader').innerText;
  const fsSource = document.getElementById('fragmentShader').innerText;
  initShaders(gl, vsSource, fsSource);

  const vertices = new Float32Array([
    0.0, 0.1,
    -0.1, -0.1,
    0.1, -0.1
  ]);

  const vertexBuffer = gl.createBuffer();
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer);
  gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STATIC_DRAW);
  const a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0);
  gl.enableVertexAttribArray(a_Position);

  const u_Matrix = gl.getUniformLocation(gl.program, 'u_Matrix');
  let angle = 0.5;
  const sinB = Math.sin(angle);
  const cosB = Math.cos(angle);
  const matrix = [
    cosB, sinB,
    -sinB, cosB
  ];
  gl.uniformMatrix2fv(u_Matrix, false, matrix);
  gl.clearColor(0.0, 0.0, 0.0, 1.0);
  gl.clear(gl.COLOR_BUFFER_BIT);
  gl.drawArrays(gl.TRIANGLES, 0, 3);

  !(function animate() {
    angle += 0.05;
    const sinB = Math.sin(angle);
    const cosB = Math.cos(angle);
    const matrix = [
      cosB, sinB,
      -sinB, cosB
    ];
    gl.uniformMatrix2fv(u_Matrix, false, matrix);
    gl.clear(gl.COLOR_BUFFER_BIT);
    gl.drawArrays(gl.TRIANGLES, 0, 3);
    requestAnimationFrame(animate);
  })()
</script>
  • 以上是最简单的二维矩阵，我们也可以给顶点着色器一个四维矩阵

四维矩阵在着色器里的处理

  • 应用原理和二维矩阵是一样的

1 ）核心代码

<script id="vertexShader" type="x-shader/x-vertex">
    attribute vec4 a_Position;
    float angle = radians(10.0);
    float cosB = cos(angle);
    float sinB = sin(angle);
    mat4 m4 = mat4(
      cosB, sinB, 0.0, 0.0,
      -sinB, cosB, 0.0, 0.0,
      0.0, 0.0, 1.0, 0.0,
      0.0, 0.0, 0.0, 1.0
    );
    void main() {
      gl_Position = m4 * a_Position;
    }
</script>

2 ）完整代码

<canvas id="canvas"></canvas>
<script id="vertexShader" type="x-shader/x-vertex">
  attribute vec4 a_Position;
  float angle = radians(10.0);
  float cosB = cos(angle);
  float sinB = sin(angle);
  // 列主序
  mat4 m4 = mat4(
    cosB, sinB, 0.0, 0.0,
    -sinB, cosB, 0.0, 0.0,
    0.0, 0.0, 1.0, 0.0,
    0.0, 0.0, 0.0, 1.0
  );
  void main() {
    gl_Position = m4 * a_Position;
  }
</script>
<script id="fragmentShader" type="x-shader/x-fragment">
  void main() {
    gl_FragColor = vec4(1.0, 1.0, 0.0, 1.0);
  }
</script>
<script type="module">
  import { initShaders } from './utils.js';

  const canvas = document.getElementById('canvas');
  canvas.width = window.innerWidth;
  canvas.height = window.innerHeight;
  const gl = canvas.getContext('webgl');

  const vsSource = document.getElementById('vertexShader').innerText;
  const fsSource = document.getElementById('fragmentShader').innerText;
  initShaders(gl, vsSource, fsSource);

  const vertices = new Float32Array([
    0.0, 0.1,
    -0.1, -0.1,
    0.1, -0.1
  ])

  const vertexBuffer = gl.createBuffer();
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer);
  gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STATIC_DRAW);
  const a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0);
  gl.enableVertexAttribArray(a_Position);

  gl.clearColor(0.0, 0.0, 0.0, 1.0);
  gl.clear(gl.COLOR_BUFFER_BIT);
  gl.drawArrays(gl.TRIANGLES, 0, 3);
</script>

用js向顶点着色器传递四维矩阵

1 ）核心代码

const u_Matrix = gl.getUniformLocation(gl.program, 'u_Matrix');
let angle = 0.1;
const [sinB, cosB] = [Math.sin(angle), Math.cos(angle)];
const matrix = [
    cosB, sinB, 0.0, 0.0,
    -sinB, cosB, 0.0, 0.0,
    0.0, 0.0, 1.0, 0.0,
    0.0, 0.0, 0.0, 1.0
];
gl.uniformMatrix4fv(u_Matrix, false, matrix);

2 ）完整代码

<canvas id="canvas"></canvas>
<script id="vertexShader" type="x-shader/x-vertex">
  attribute vec4 a_Position;
  // 列主序
  uniform mat4 u_Matrix;
  void main() {
    gl_Position = u_Matrix * a_Position;
  }
</script>
<script id="fragmentShader" type="x-shader/x-fragment">
  void main() {
    gl_FragColor = vec4(1.0,1.0,0.0,1.0);
  }
</script>
<script type="module">
  import { initShaders } from './utils.js';

  const canvas = document.getElementById('canvas');
  canvas.width = window.innerWidth;
  canvas.height = window.innerHeight;
  const gl = canvas.getContext('webgl');

  const vsSource = document.getElementById('vertexShader').innerText;
  const fsSource = document.getElementById('fragmentShader').innerText;
  initShaders(gl, vsSource, fsSource);

  const vertices = new Float32Array([
    0.0, 0.1,
    -0.1, -0.1,
    0.1, -0.1
  ]);

  const vertexBuffer = gl.createBuffer();
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer);
  gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STATIC_DRAW);
  const a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0);
  gl.enableVertexAttribArray(a_Position);

  const u_Matrix = gl.getUniformLocation(gl.program, 'u_Matrix');
  let angle = 0.5;
  const sinB = Math.sin(angle);
  const cosB = Math.cos(angle);
  const matrix = [
    cosB, sinB, 0, 0,
    -sinB, cosB, 0, 0,
    0, 0, 1, 0,
    0, 0, 0, 1
  ];
  gl.uniformMatrix4fv(u_Matrix, false, matrix);

  gl.clearColor(0.0, 0.0, 0.0, 1.0);
  gl.clear(gl.COLOR_BUFFER_BIT);
  gl.drawArrays(gl.TRIANGLES, 0, 3);

  !(function animate() {
    angle += 0.05;
    const sinB = Math.sin(angle);
    const cosB = Math.cos(angle);
    const matrix = [
      cosB, sinB, 0, 0,
      -sinB, cosB, 0, 0,
      0, 0, 1, 0,
      0, 0, 0, 1
    ];
    gl.uniformMatrix4fv(u_Matrix, false, matrix);

    gl.clear(gl.COLOR_BUFFER_BIT);
    gl.drawArrays(gl.TRIANGLES, 0, 3);
    requestAnimationFrame(animate);
  })()
</script>

http://www.kler.cn/a/162697.html

相关文章：

  • 超市里的货物架调整（算法解析）|豆包MarsCode AI刷题
  • 10款PDF翻译工具的探索之旅：我的使用经历与工具特色！！
  • Java基础-组件及事件处理（下）
  • git之 revert和rebase
  • 无插件H5播放器EasyPlayer.js网页web无插件播放器vue和react详细介绍
  • DHCP与DNS安全管理
  • stm32串口编程实例-实现数据的收发功能
  • 【CVE 复现】CVE-2022-0185 fsconfig之整数溢出
  • LinuxBasicsForHackers笔记 -- 使用和滥用服务
  • 自动化测试框架需要具备哪些功能？
  • 2、Redis变慢原因排查(下)
  • 使用Echarts.js绘制环形图（指定触发高亮事件）
  • Python中读写（解析）JSON文件的深入探究
  • MIT线性代数笔记-第26讲-对称矩阵及正定性
  • VUE学习二、创建一个前端项目
  • vs 安装 qt qt扩展 改迅雷下载qt
  • java中可重入锁的作用是什么？
  • Linux 统计命令Netstat详解
  • jsonwebtoken生成token和解析
  • 进制 + 原码，反码，补码
  • 供应链产品经理常用的ChatGPT通用提示词模板
  • 代立冬：基于Apache Doris+SeaTunnel 实现多源实时数据仓库解决方案探索实践
  • 持续集成交付CICD：CentOS 7 安装 Sonarqube9.6
  • 使用Java API操作HDFS
  • 云上巴蜀丨云轴科技ZStack成功实践精选（川渝）
  • Leetcode—2034.股票价格波动【中等】