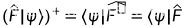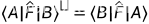狄拉克符号系统
狄拉克符号系统:
狄拉克构造了一个抽象的、一般矢量--态矢和一整套狄拉克符号以描述量子力学体系的状态
一般狄拉克符号
任何力学量的完全集的本征函数系
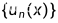 作为基矢构成希尔伯特空间,微观体系的状态波函数
作为基矢构成希尔伯特空间,微观体系的状态波函数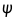 作为该空间的一个态矢,有且仅有
作为该空间的一个态矢,有且仅有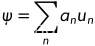 。态矢在所有基矢上的分量构成态矢在这个表象中的表示。微观体系所有可以实现的状态都与此空间中某个态矢相对应,故称该空间为态空间。
。态矢在所有基矢上的分量构成态矢在这个表象中的表示。微观体系所有可以实现的状态都与此空间中某个态矢相对应,故称该空间为态空间。
右矢,左矢,右矢空间,左矢空间
右矢: ket矢,bra矢,bracket括号
同一表象中,右矢和左矢的分量互为共轭复数
狄拉克符号体系下:任意两个态矢的内积定义为同一表象下伴随空间中相应分量之积的和

离散谱基矢
正交归一性
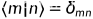
展开定理
同时左乘一个左矢:
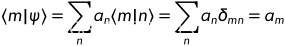
封闭性

连续谱基矢
正交归一性
展开定理
封闭性
态矢和波函数
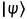 表示一个抽象的态矢
表示一个抽象的态矢
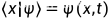 为x表象的波函数
为x表象的波函数
态矢在基矢下的形式
离散谱基矢
基矢为
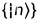 ,态矢记为
,态矢记为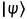 ,用基矢展开
,用基矢展开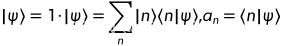
展开系数构成态矢在基矢表象中的分量,即
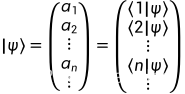
其相应的左矢
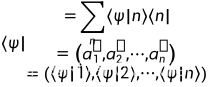
连续谱基矢
算符
需要背下来的一些玩意

本征值方程,本征值与本征函数
厄米算符

一个算符经厄米运算之后不变,则称为厄米算符,可观测量都是厄米算符
对偶
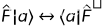
线性厄米算符的作用
离散谱基矢
算符在基矢上的作用
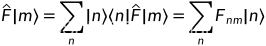
其中:有算符矩阵元
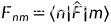
算符在态矢上的作用(算符方程)

连续谱基矢
算符对左矢空间的作用
算符对左矢空间的态矢从后向前作用: