人的全面发展评价指标体系—基于相关-主成分分析构建

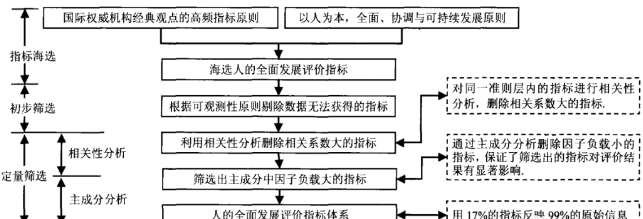
本文先从经济、社会、生活质量和人口素质四个方面海选了众多人的全面发展评价指标,然后根据可观测性原则剔除无法获得的指标进行了初步筛选,再利用相关性分析删除相关系数大的指标,以及通过主成分分析删除因子负载小的指标,完成了定量筛选,最终构建了由14个变量组成的评价指标体系,利用17%的指标反映了99%的原始信息。
一、 筛选步骤
1.海选出大量指标,并进行标准化
2.根据可观测性原则删除无法获得的评价指标
此步骤删除指标:

3.通过相关性分析删除同一准则层内相关系数大的指标
此步骤删除指标:

4.通过主成分分析删除了因子负载小的指标
此步骤删除指标:
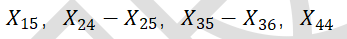
二、 合理性判定标准
构建指标的信息贡献率:

为指标数据的协方差矩阵;为协方差矩阵的迹;为筛选后的指标个数;为海选指标的个数。
如果用30%以下的海选指标反映了95%以上的原始信息,则认为指标体系构建合理。
三、 结果
从海选指标中最终保留了人均GDP、城镇居民可支配收入、农民人均纯收入、农村居民非农就业率、基尼系数、社会保障覆盖率、每万人医生数、国民幸福指数、恩格尔系数、人均住房面积、人均绿地面积、平均受教育年限、科技文卫支出/GDP、每万人拥有科技人员数等14个指标。最终信息贡献率为98.9%。
数据概况:

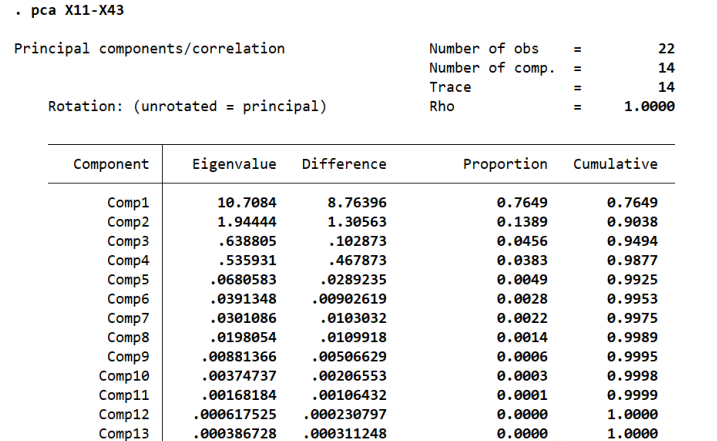
以下为我们对筛选后指标进行的主成分分析实证结果:
1.判断是否适合做主成分分析


先对变量进行相关性分析,得到所有变量之间的方差-协方差矩阵。可以发现很多变量之间的相关关系是非常强的甚至有的超过了90%,这说明变量之间存在着相当数量的信息重叠。并且SMC与KMO检验得到的结果表明变量的线性关系很强。进行主成分分析把众多的初始变量整合成少数几个相互之间无关的主成分变量是非常必要的。
2.主成分分析
结果可以发现,stata总共提取了14个主成分。可以发现第一个主成分的方差贡献率是0.7649,表示该主成分解释了所有变量的76.49%的信息。
只保留特征值大于1的主成分:
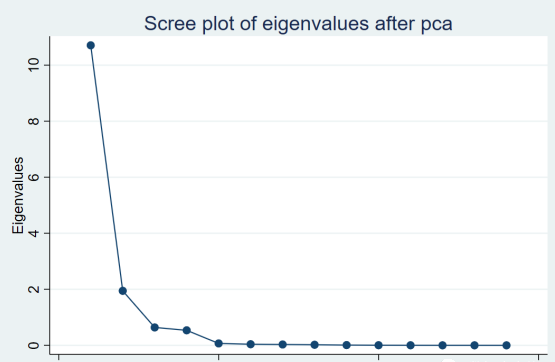
碎石图:
screeplot
载荷图:
loadingplot

包含内容:

相关数据请见评论
