【GAMES101】04 Viewing Transformation
1.View/Camera Transformation(视图变换)
1、将准备拍摄的对象移动到场景中指定位置。(模型变换,Model Transform) - 模型导入场景中从模型坐标系转换成世界坐标系
2、将相机移动到准备拍摄的位置,将它对准某个方向。(视图变换,View Transform)- 从世界坐标系转换成相机坐标系
3、设置相机的焦距,或者调整缩放比例。(投影变换,Projection Transform)
(跟现实做的变换一样,简称MVP变换)
怎么进行视图变换(如何确定相机的摆放)
- 定义相机的位置
- 往哪看
- 相机向上的方向(固定相机的旋转 )
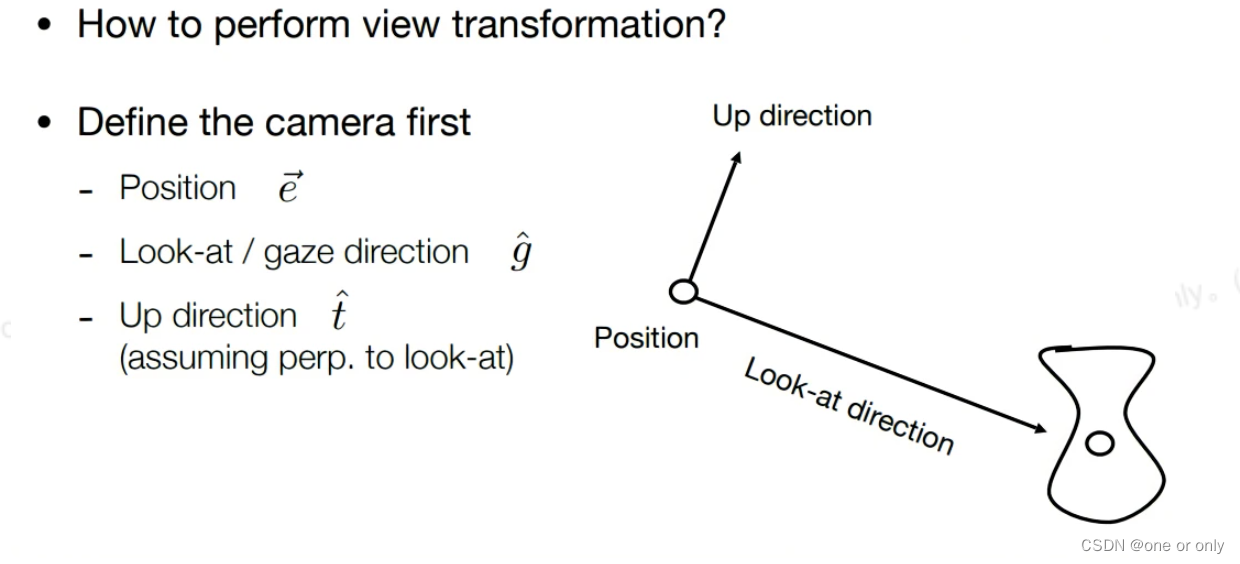
相当于定义了一个坐标系,将相机移动到一个固定的位置上,可以使操作简化(相机原点在000,相机y轴向上,永远往-z轴看)。
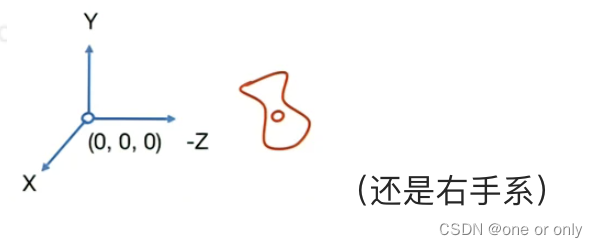

(图的意思是,不好求将摄像机旋转到原点的矩阵,可以逆过来将原点位置的摄像机旋转到e的位置的矩阵,再求逆矩阵)
Q:如何求逆矩阵呢
A:旋转矩阵就是正交矩阵,即求它的转置矩阵就是逆矩阵了
Summary:
①相机物体都应用同样的变换,只要相机能移动到规定的位置上,那么物体自然就落在需要它们所在的位置上。
②模型变换和视图变换经常被一起叫作模型视图变换(Also know as ModelView Translation)。
2.Projection transformation (投影变换)
投影变换主要分为正交投影和透视投影。这两者的区别,透视投影的投影结果是“近大远小”;正交投影的投影结果是模型相对大小不变。透视投影的结果,与我们人眼看见物品的方式是一样的。正交投影一般应用于工程作图,如建房蓝图等。
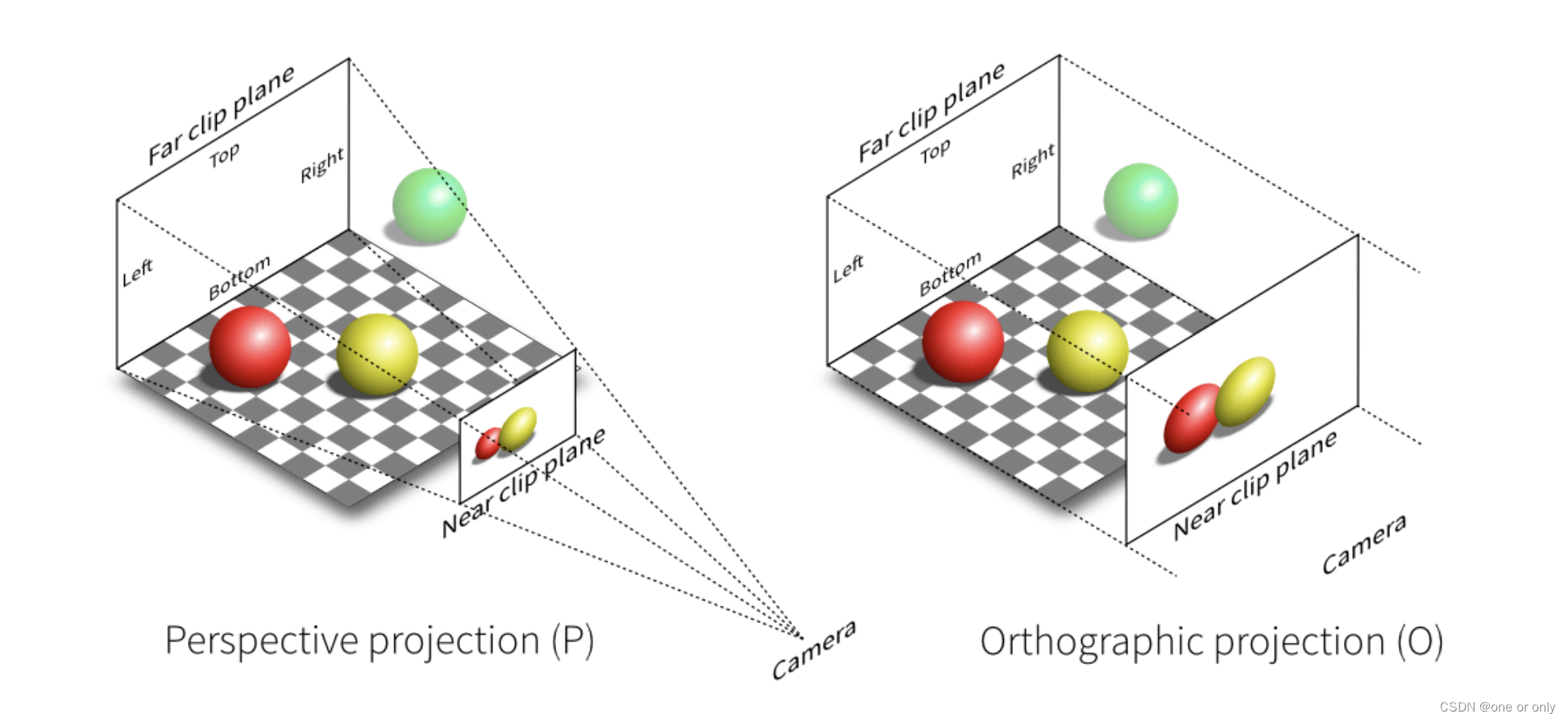
- 透视投影(Perspective Projection):摄像机认为是一个点,在空间中连出一个四棱锥,这个区域内的所有东西都显示在一个平面上。
- 正交投影(Orthographic Projection):假设相机离得无限远,(假如将透视投影的相机拿得无限远的时候,这时候近处平面与远处平面的物体大小是几乎完全一样)。

