算法：递归启蒙-汉诺塔

基本所有的讲递归的书和视频都会以汉诺塔作为开始，因为它足够经典

汉诺塔问题要求整个挪动的过程中都符合小压大的原则，就是如果同一个柱子上有超过1个的话，那必须下面是最大的，上面依次变小，不能出现大盘压小盘的情况。

n层汉诺塔问题解题思路

1.先把n-1个盘从左挪到中

2.把第n个盘从左挪到右

3.把1～n-1从中挪到右。

3层汉诺塔的具体步骤

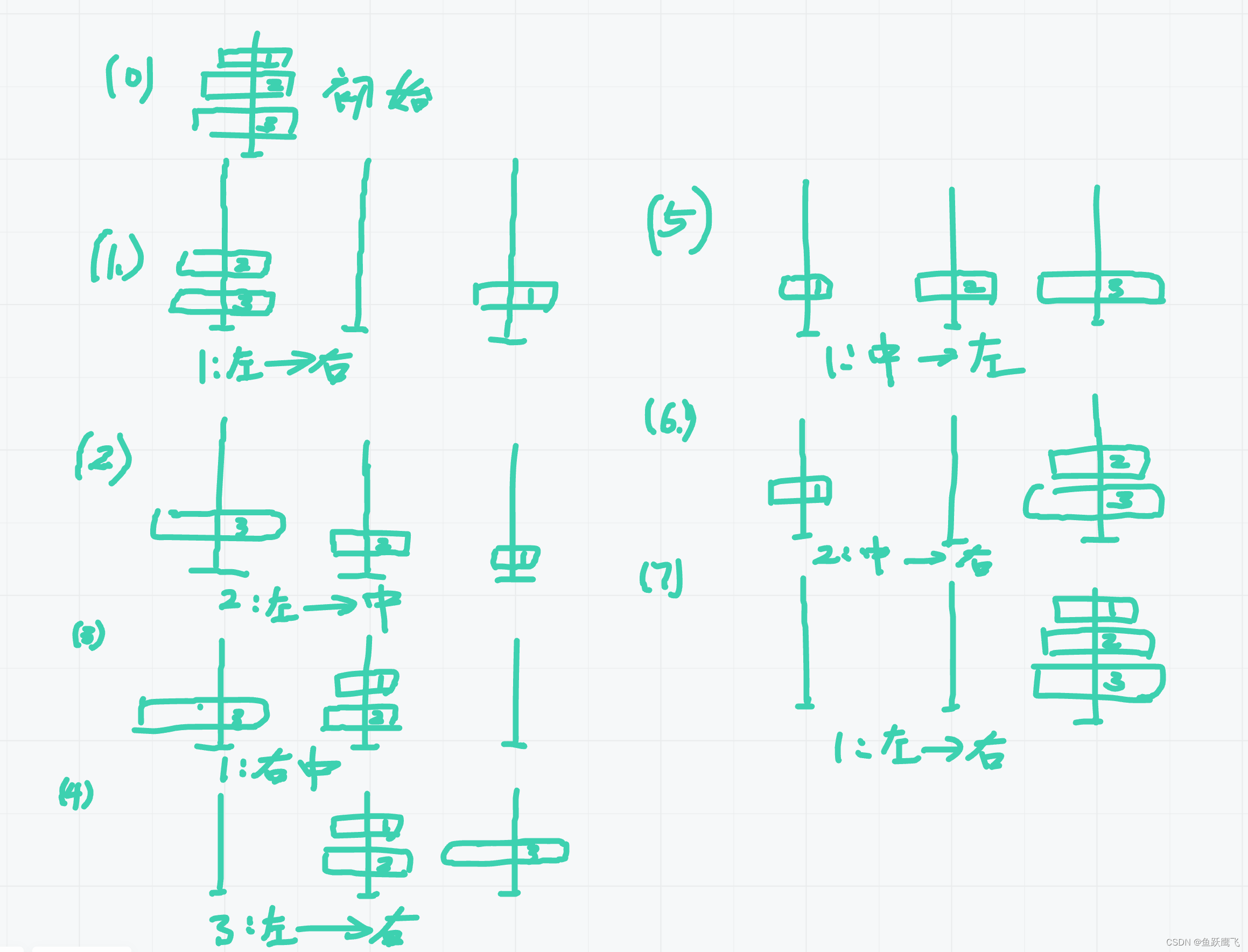
 粗糙版代码：
 

package dataStructure.recurrence.practice;

public class Hanoi {
    public static void leftToRight(int n) {
        if(n == 1) {
            System.out.println("move 1 from left To Right");
            return;
        }
        leftToMiddle(n-1);
        System.out.println("move " + n + " from left to right");
        middleToRight(n - 1 );
    }

    public static void leftToMiddle(int n) {
        if(n == 1) {
            System.out.println("move 1 from left to middle");
            return;
        }
        leftToRight(n - 1);
        System.out.println("move " + n + " from left to middle");
        rightToMiddle(n - 1);

    }

    public static void middleToLeft(int n) {
        if(n == 1) {
            System.out.println("move 1 from middle to left");
            return;
        }
        middleToRight(n - 1);
        System.out.println("move " + n + " from middle to left");
        rightToLeft(n - 1);
    }

    public static void middleToRight(int n) {
        if(n == 1) {
            System.out.println("move 1 from middle to right");
            return;
        }
        middleToLeft(n -1 );
        System.out.println("move " + n + " from middle to right");
        leftToRight(n - 1);
    }

    public static void rightToLeft(int n) {
        if(n == 1) {
            System.out.println("move 1 from right to left");
            return;
        }
        rightToMiddle(n - 1 );
        System.out.println("move " + n + " from right to left");
        middleToLeft(n - 1);
    }

    public static void rightToMiddle(int n) {
        if(n == 1) {
            System.out.println("move 1 from right to middle");
            return;
        }
        rightToLeft(n - 1);
        System.out.println("move " + n + " from right to middle");
        leftToMiddle(n - 1);
    }

    public static void main(String[] args) {
        leftToRight(3);
    }
}

代码中枚举了6种可能性的移动，每个都写了一个方法，显然有些臃肿，我们可以通过增加参数来让方法拥有更多的功能。

改进后的正常版的汉诺塔代码

package dataStructure.recurrence.practice;

public class Hanoi2 {
    public static void move(int n, String from, String to, String other) {
        if(n == 1) {
            System.out.println("move 1 from " + from + " to " + to  );
        } else {
            move(n - 1, from, other, to);
            System.out.println("move " + n + " from " + from + " to " + to);
            move(n - 1, other, to, from);
        }
    }

    public static void main(String[] args) {
        move(3, "left", "right", "middle");
    }
}

运行结果：

move 1 from left to right
move 2 from left to middle
move 1 from right to middle
move 3 from left to right
move 1 from middle to left
move 2 from middle to right
move 1 from left to right

Process finished with exit code 0