【基础算法】数组相关题目

系列综述：
💞目的：本系列是个人整理为了秋招算法的，整理期间苛求每个知识点，平衡理解简易度与深入程度。
🥰来源：材料主要源于代码随想录进行的，每个算法代码参考leetcode高赞回答和其他平台热门博客，其中也可能含有一些的个人思考。
🤭结语：如果有帮到你的地方，就点个赞和关注一下呗，谢谢🎈🎄🌷！！！
🌈数据结构基础知识总结篇

😊点此到文末惊喜↩︎

二分查找

基本二分法

1. 二分法前提（有序无重复的数组）
   • 数组有序：一次比较即可确定需要查找的那一半，效率高的关键
   • 数组中无重复元素：一旦有重复元素，使用二分查找法返回的元素下标可能不是唯一
   • 查找对象为数组：数组可以进随机存取
2. 边界处理方式
   • 左闭右闭 [left, right]：基本算法，可以定位后再寻找相同元素区域的左右边界
   • 左闭右开 [left, right)：可以在存在相同元素时，定位到相同元素区域的 左右边界
3. leetcode题目：704. 二分查找
   

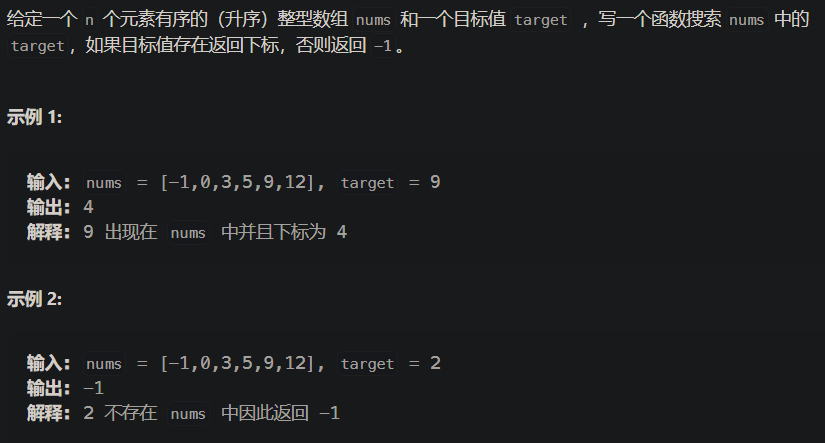
   // *****************前闭后闭的基本二分查找，可以代替下一种*******************
   int search(vector<int>& nums, int target) {
   // 0. 健壮性检查
       if(nums.size() <= 0) return -1;
   // 1. 定义边界指针（指向遍历数组区域的边界位置）
       int left = 0;
       int right = nums.size() - 1; // 定义target在左闭右闭的区间里
   // 2. 基本算法步骤的循环    
       while (left <= right) { // 前闭后闭用<=
       	// - 定义
           int mid = left + ((right - left)>>2);// 防止溢出 等同于(left + right)/2
           // 目标值在左区间
           if (target < nums[mid]) {
               right = mid - 1; 
           // 目标值在右区间
           } else if (target > nums[mid]) {
               left = mid + 1; 
           // 找到目标值，即相等时
           } else {
               return mid; // 数组中找到目标值，直接返回下标
           }
       }
   // 3. 添加进行左右边界的定位操作
   	// ...
       return -1;// 未找到目标值
   }
   

   • mid = L + ((R - L)>>1)
     • 防溢出：如果L 和 R太大，直接相加就有溢出的可能
     • 移位：等价于除法算法，但是效率高
   • 使用前闭后闭的二分区域查找，可以在查找target位置后再进行相同元素相连区域的定位操作。

搜索插入位置

1. 该题与二分查找类似，但是最后返回的是插入的位置，所以没找到时应该返回的是最后比较的位置的后一个
2. leetcode题目：35. 搜索插入位置
   

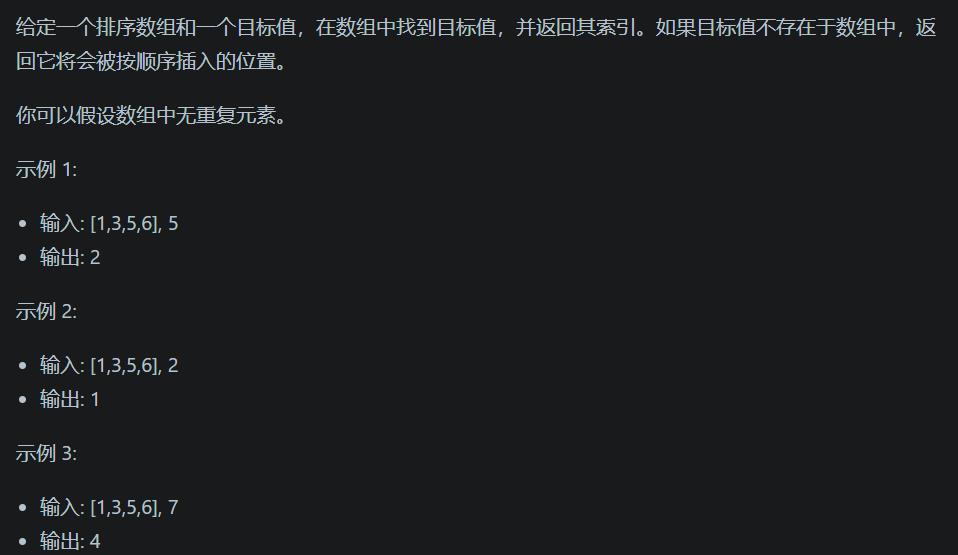
   class Solution {
   public:
       int searchInsert(vector<int>& nums, int target) {
           int left = 0;
           int right = nums.size()-1;
           while (left <= right){
               int mid = left + ((right-left) >> 2);
               if(target < nums[mid]){
                   right = mid - 1;
               }else if(target > nums[mid]){
                   left = mid + 1;
               }else{
                   return mid;
               }
           }
           return left;// left为相等值未找到时应插入的位置
       }
   };
   

在排序数组中查找元素的第一个和最后一个位置

1. 该题与二分查找类似，但是最后应该对于相邻相同元素的起始和末尾进行遍历判断
2. leetcode题目：35. 搜索插入位置
   

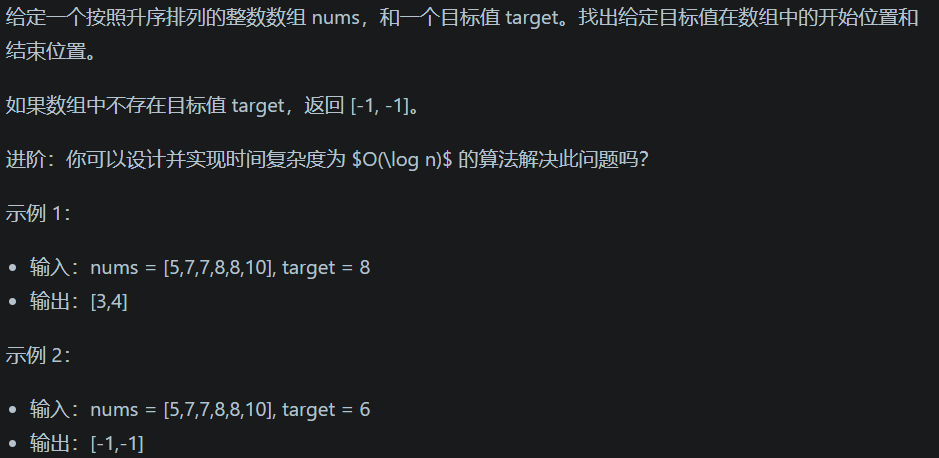
   vector<int> searchRange(vector<int>& nums, int target) {
       vector<int> res(2,-1);// 初始化两个值为-1的元素
       if(nums.size() <= 0) return res; 
       // 基本二分法
       int left = 0;
       int right = nums.size()-1;
       int mid;
       while(left <= right){
           mid = left + ((right -left) >> 2);
           if(target < nums[mid]){
               right = mid - 1;
           }else if(target > nums[mid]){
               left = mid + 1;
           }else{
               break;// 保留mid
           }
       }
      	// 寻找相似相邻区间的左右边界
       int l = mid;
       int r = mid;
       if(nums[mid] != target){
           return res;
       }else{
           while (l > 0){
               if(nums[l] == nums[l-1]){
                   l--;
               }else
                   break;
           }
           while (r < nums.size()-1){
               if(nums[r] == nums[r+1]){
                   r++;
               }else
                   break;
           }
       }
       cout << res[0]<< endl;
       res[0]=l;
       res[1]=r;
       return res;
   
   }
   

快慢指针

移除元素

1. 快慢指针
   • 快指针fast用于条件判断
   • 慢指针slow用于位置保存
2. leetcode题目：27. 移除元素

   给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。
   不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并原地修改输入数组。
   元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
   示例 1: 给定 nums = [3,2,2,3], val = 3, 函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。 你不需要考虑数组中超出新长度后面的元素。
   示例 2: 给定 nums = [0,1,2,2,3,0,4,2], val = 2, 函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 你不需要考虑数组中超出新长度后面的元素。

   int removeElement(vector<int>& nums, int val) {
   	// 快慢指针
       int slow = 0;
       int fast = slow;
       
       while(fast < nums.size()){
           if(nums[fast] == val){
           // 如果元素值为val，快指针选择下一个
               ++fast;
           }else{
           // 如果找到非val元素，将该元素赋值给nums[slow]
               nums[slow] = nums[fast];
               ++slow;
               ++fast;
           }
       }
       return slow;
   }
   

有序数组的平方

1. 循环不变量（循环中的变量的逻辑）
   • 初始化： 迭代前，循环不变量为真
   • 保持： 迭代中，前后状态的转移仍然能保证循环不变量为真
   • 终止： 迭代后，循环不变量可以提供有用结果
2. 逆向思维，充分利用不变的逻辑进行程序的简化。如下题中的从后向前和从两边向中间的遍历方式。
3. leetcode题目：977. 有序数组的平方
   

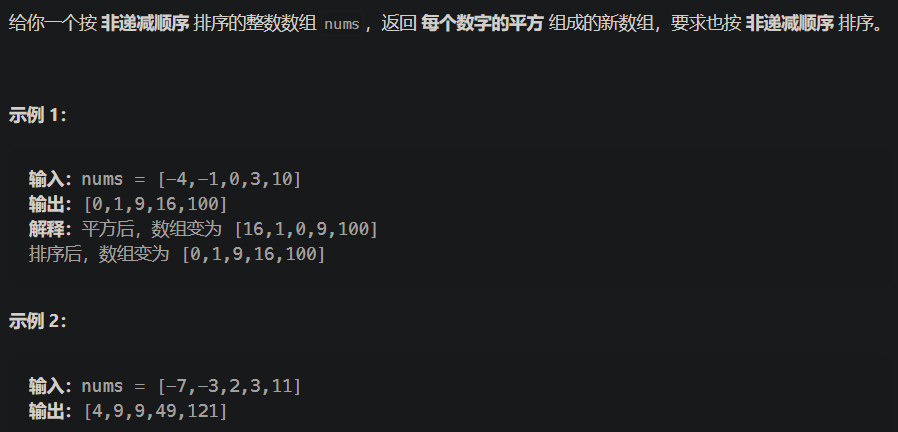
   vector<int> sortedSquares(vector<int>& nums) {
       // 用双指针指向两端，从两端向中间进行逼近
       int left = 0;
       int right = nums.size()-1;
       // 从后向前将每次比较较大的填入新的数组中
       vector<int> res(nums);
       int index = right;
   
       while (left <= right) {
           if (nums[left] * nums[left] > nums[right] * nums[right]) {
               res[index--] = nums[left] * nums[left];
               ++left;
           } else {
               res[index--] = nums[right] * nums[right];
               --right;
           }
       }
   
       return res;
   }
   
   

滑动窗口

移除元素

1. 滑动窗口：不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果

2. 滑动窗口基本框架

   void slidwindow(vector<int> nums)
   {
   	// 1. 窗口区间为[left, right)
       int left = 0;
       int right = 0;
       // 2. 直到到达窗口右边界
       while(right < nums.size())
       {
       	// - 扩大右边界并更新窗口状态
           ...
           right++;
           // - 窗口到达什么状态需要收缩
           while(需要收缩)
           {
           // - 缩小左边界并更新窗口状态
               ...
               left++;
           }
       }
   }
   

3. leetcode题目：209. 长度最小的子数组
   

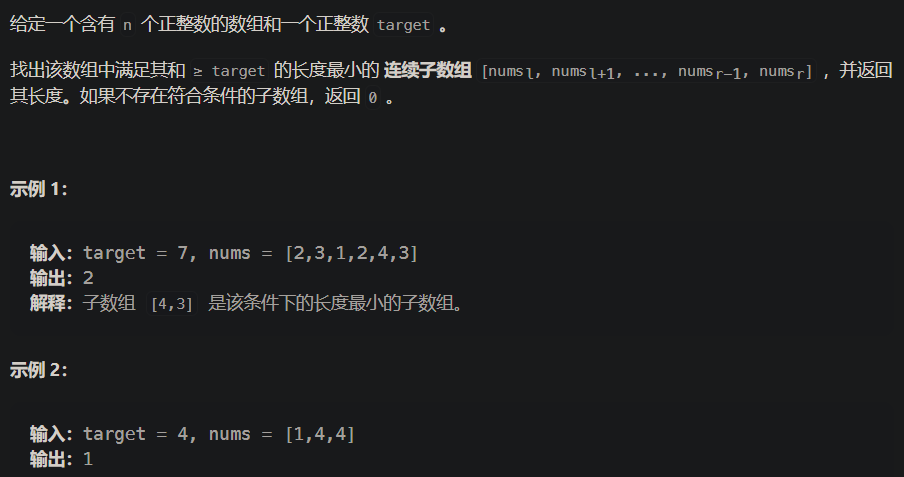
   int minSubArrayLen(int target, vector<int>& nums) {
       int left = 0;
       int right = 0; 
       int res = INT_MAX;
       int len = 0;
       int windows_sum = 0;
       while(right < nums.size())//窗口区间为[left, right)
       {
           windows_sum += nums[right];//更新窗口状态
           right++;
           while(windows_sum >= target)//收缩窗口
           {
               len = right - left;
               res = min(res, len);
               windows_sum -= nums[left];//更新窗口状态
               left++;
           }
       }
       return res == INT_MAX? 0:res;
   }
   

🚩点此跳转到首行↩︎

参考博客

1. leetcode二分查找
2. 代码随想录
3. 二分查找算法详解
4. 待定引用
5. 待定引用
6. 待定引用
7. 待定引用
8. 待定引用